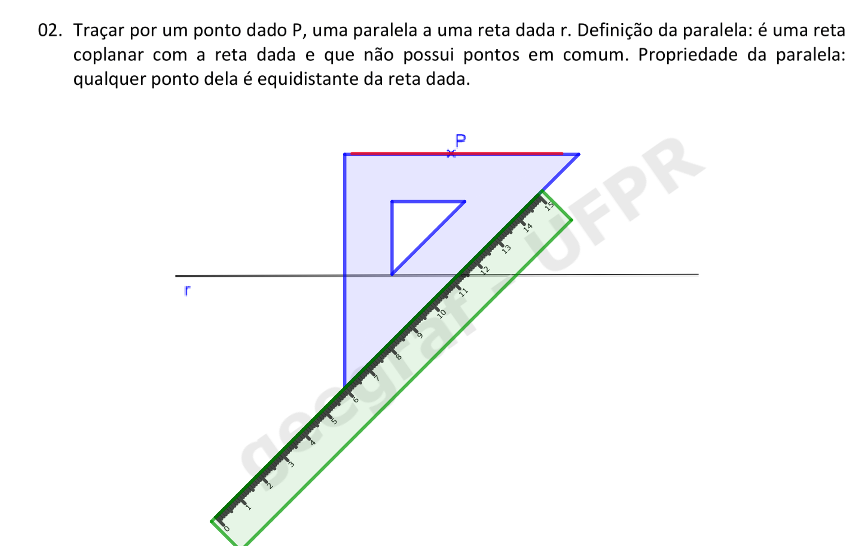
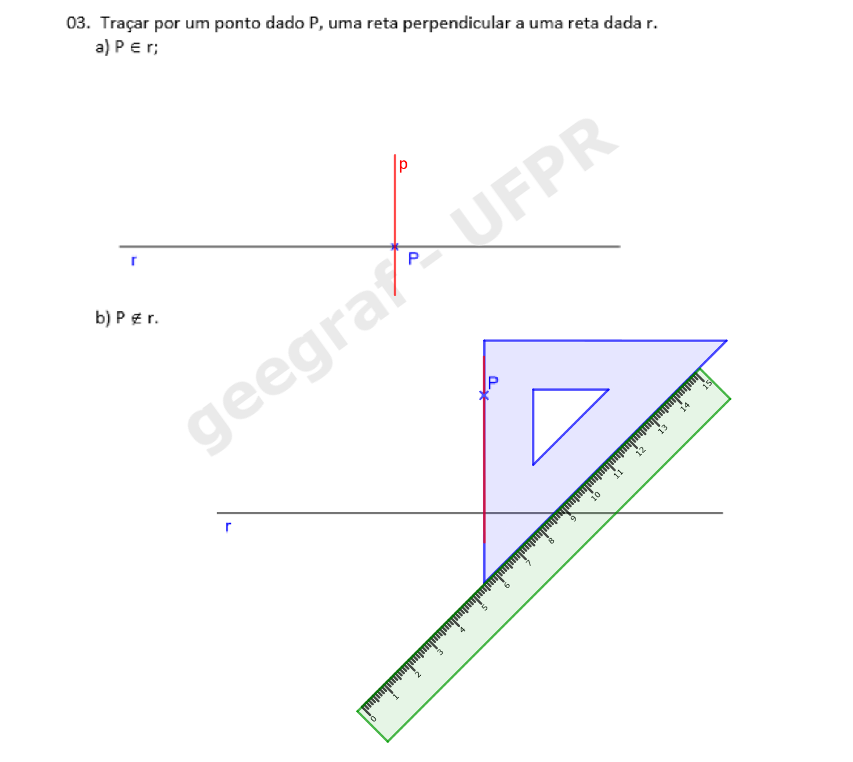
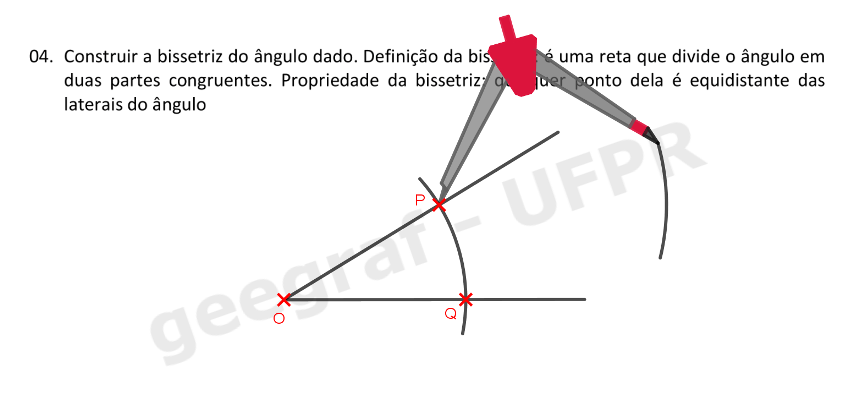
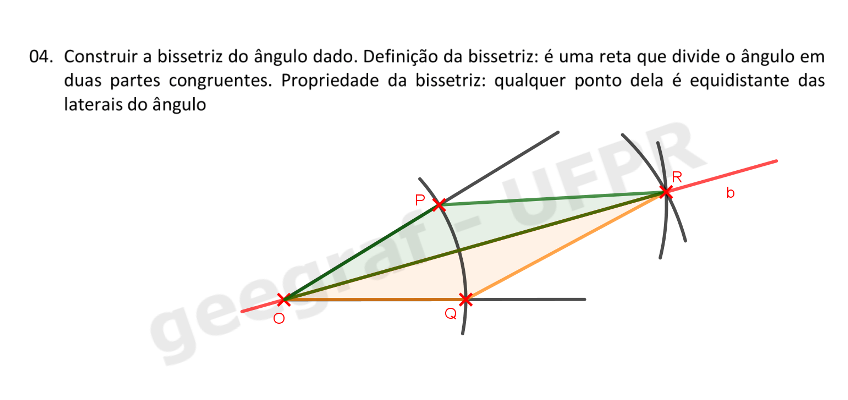
Construções Geométricas
Esta página contém definições, propriedades e os procedimentos para as construções geométricas usadas na disciplina de Desenho Geométrico II.
A apostila está disponível no link: apostila de Desenho Geométrico 2
Uso dos materiais básicos de Desenho
Veja o passo a passo das construções básicas mostradas no vídeo:

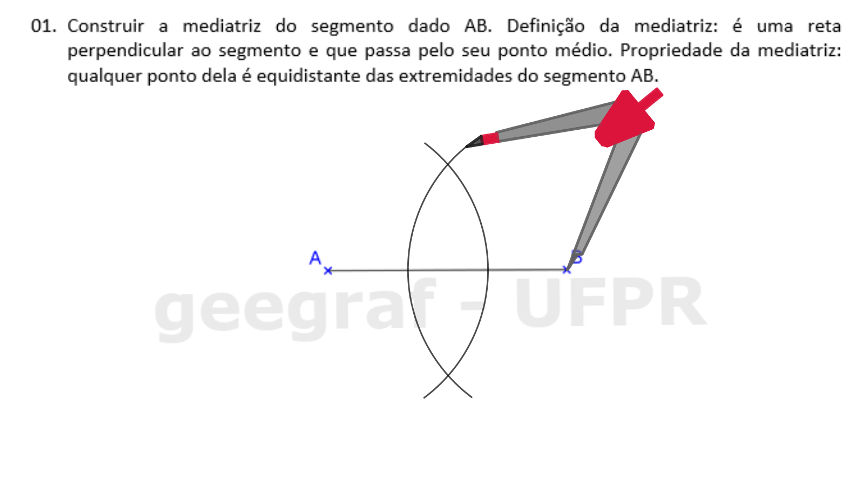
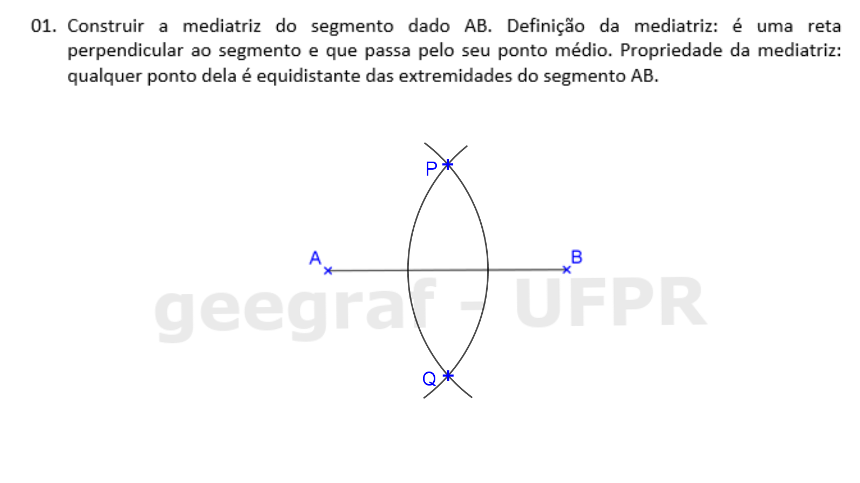
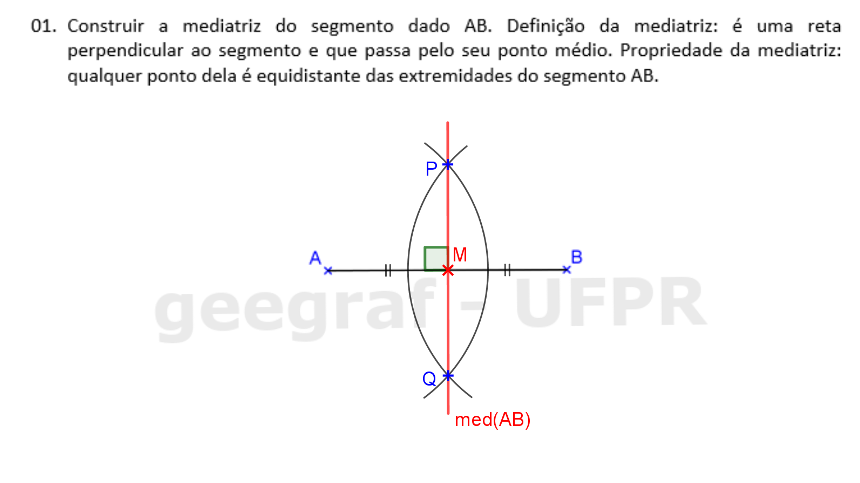
📏 📐 Resolução
Vamos utilizar a régua e o compasso para resolver este exercício. Clique nos botões do passo a passo para fazer a construção na sua apostila.


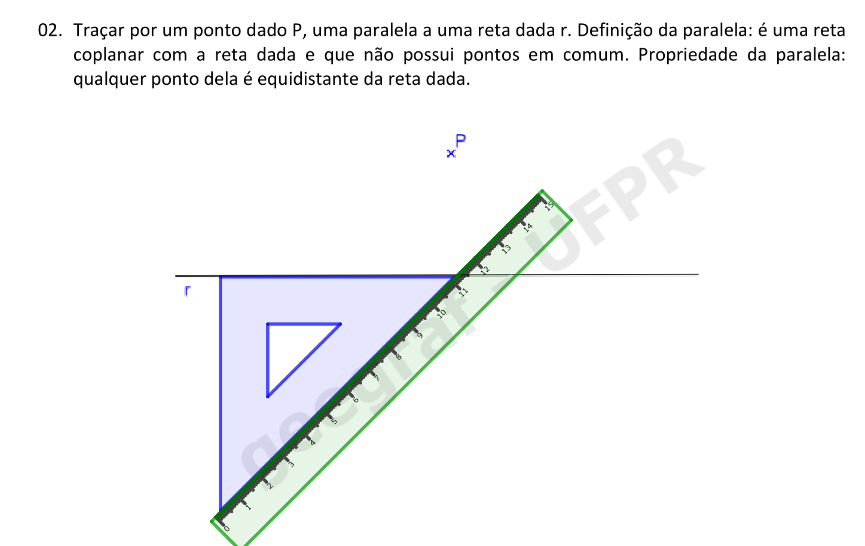
📏 📐 Resolução com esquadros
Podemos utilizar a régua e um dos esquadros ou a régua e o compasso para resolver este exercício. Primeiro, veja como é a construção com a régua e o esquadro de 45°.


📏 📐 Resolução com esquadros
Vamos utilizar a régua e um dos esquadros para resolver este exercício. Clique nos botões do passo a passo para fazer a construção na sua apostila.

📏 📐 Resolução
Vamos utilizar a régua e o compasso para resolver este exercício. Clique nos botões do passo a passo para fazer a construção na sua apostila.

1. Simetria Axial, Arcos e Ovais
Material da página 1 até a página 11.

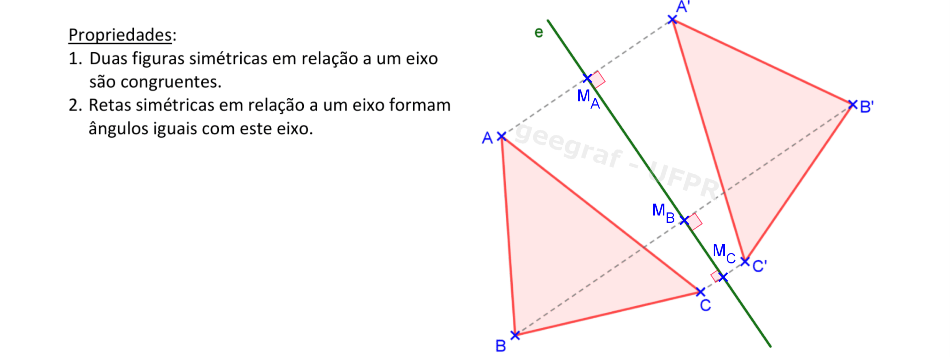
📑 Propriedades
Dados os pontos A, B e C, os simétricos destes pontos são obtidos da seguinte maneira:


📏 📐 Resolução
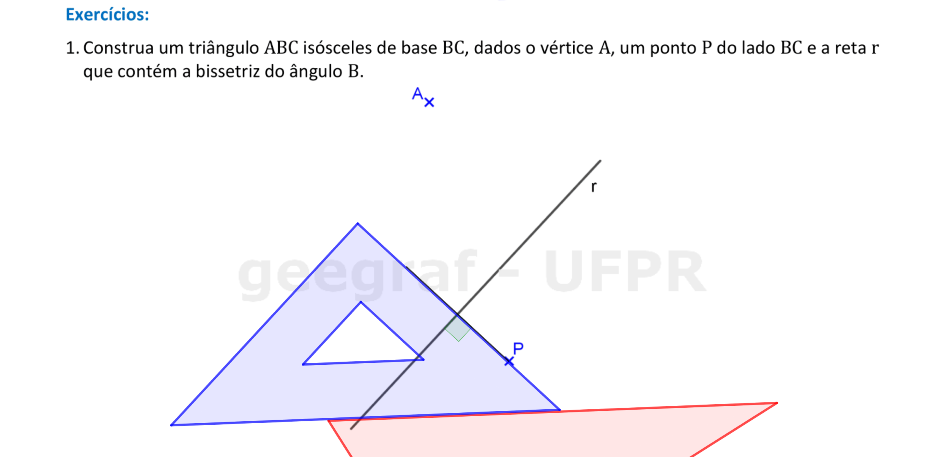
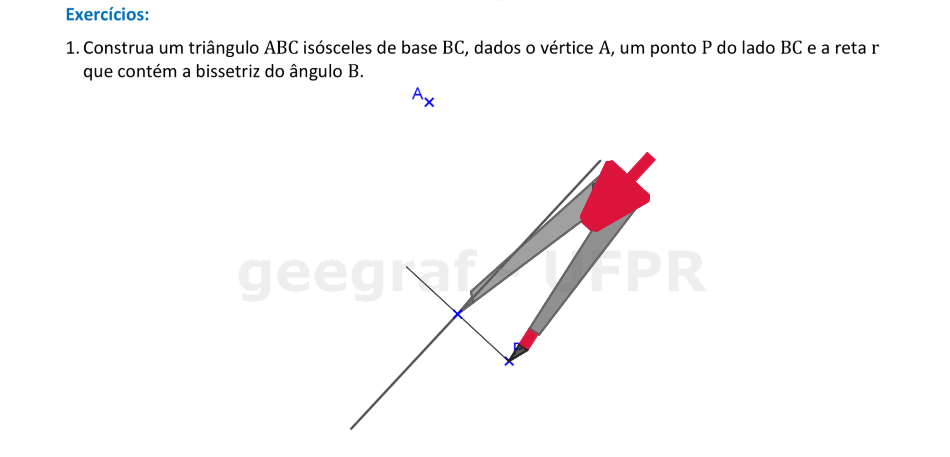
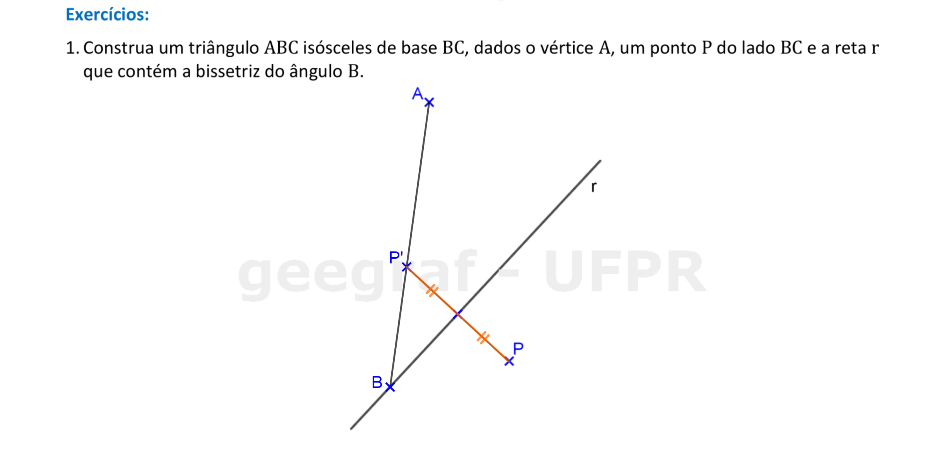
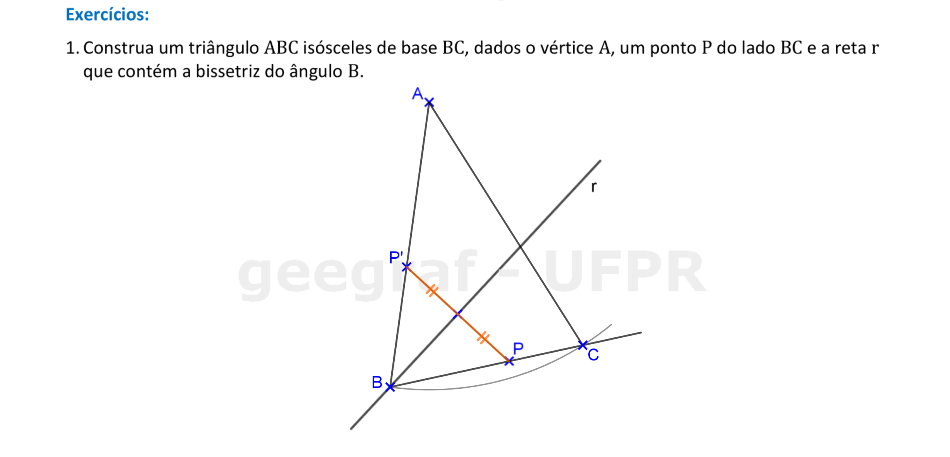
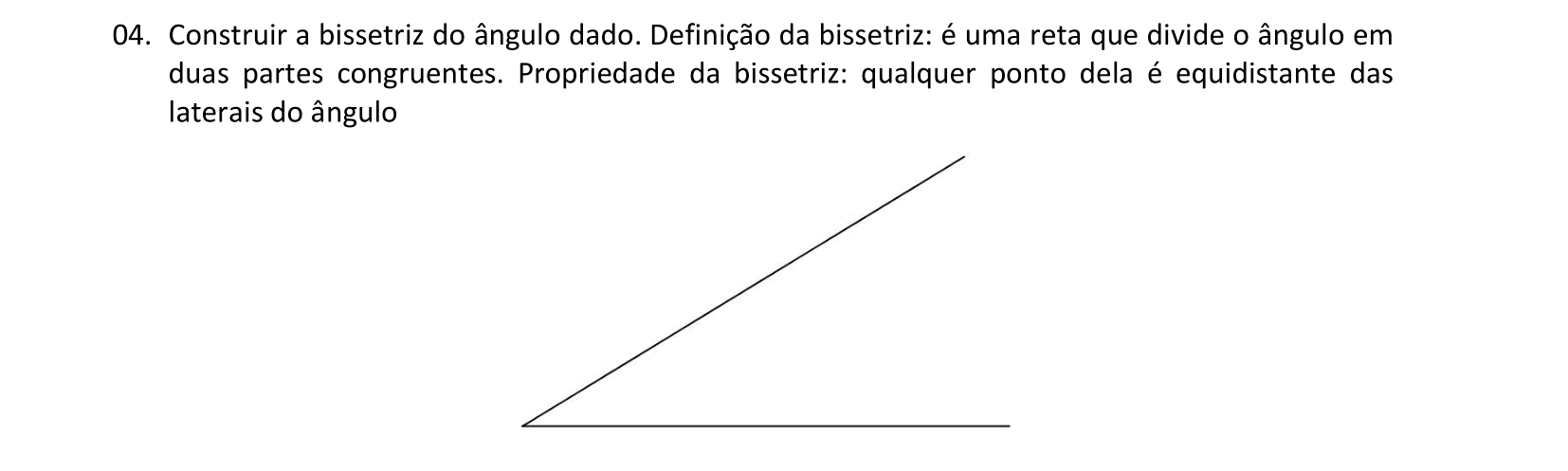
Em um triângulo, a bissetriz de um ângulo serve como eixo de simetria para os pontos dos lados adjacentes a este ângulo.

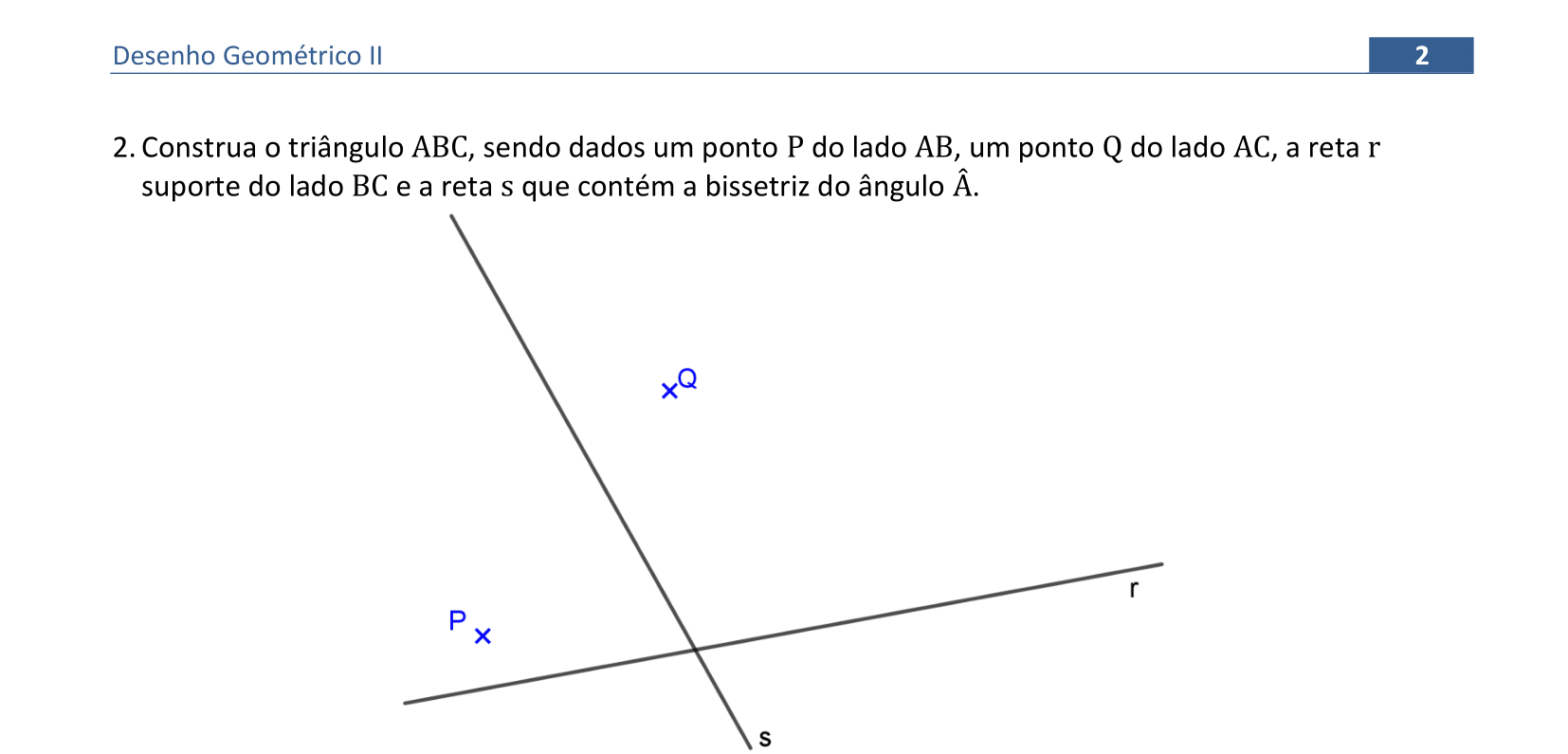
📏 📐 Resolução
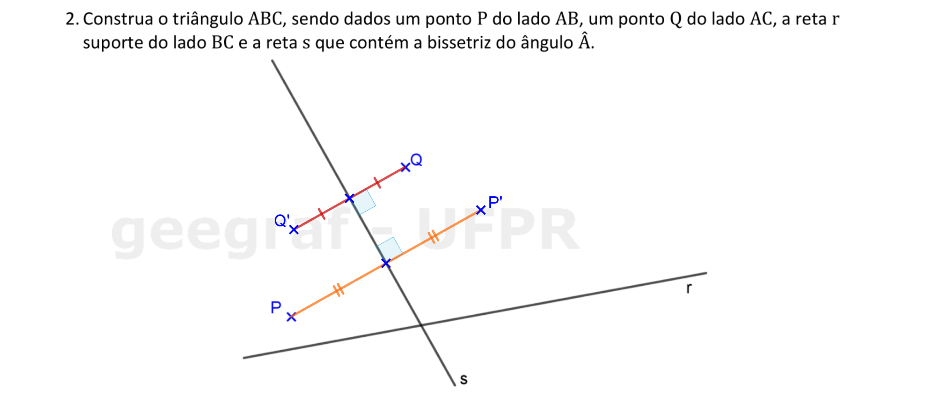
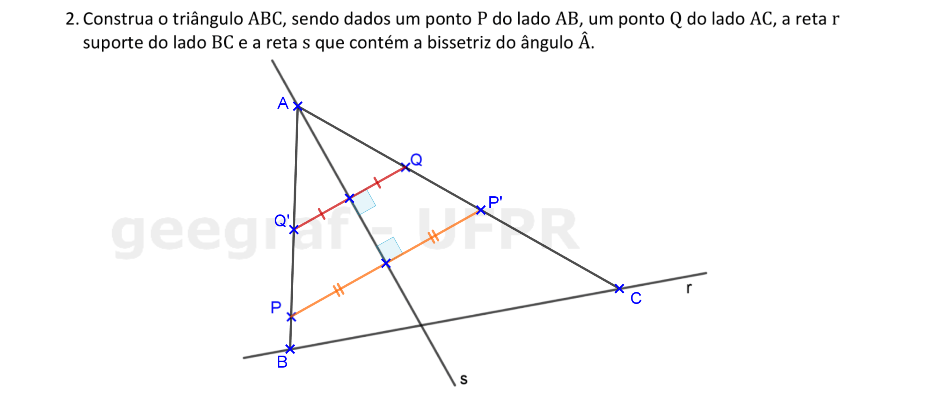
Em um triângulo, a bissetriz de um ângulo serve como eixo de simetria para os pontos dos lados adjacentes a este ângulo.


📏 📐 Resolução
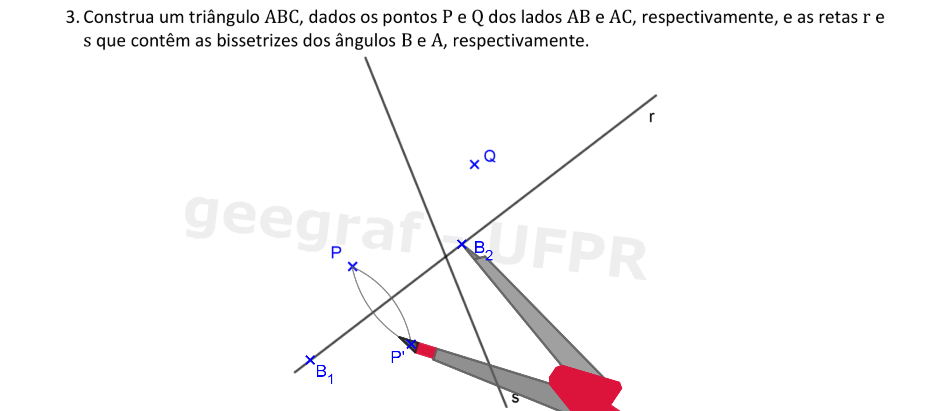
Em um triângulo, a bissetriz de um ângulo serve como eixo de simetria para os pontos dos lados adjacentes a este ângulo.


📏 📐 Resolução
Em um triângulo isósceles, a mediatriz da base serve como eixo de simetria para os pontos das laterais deste triângulo.

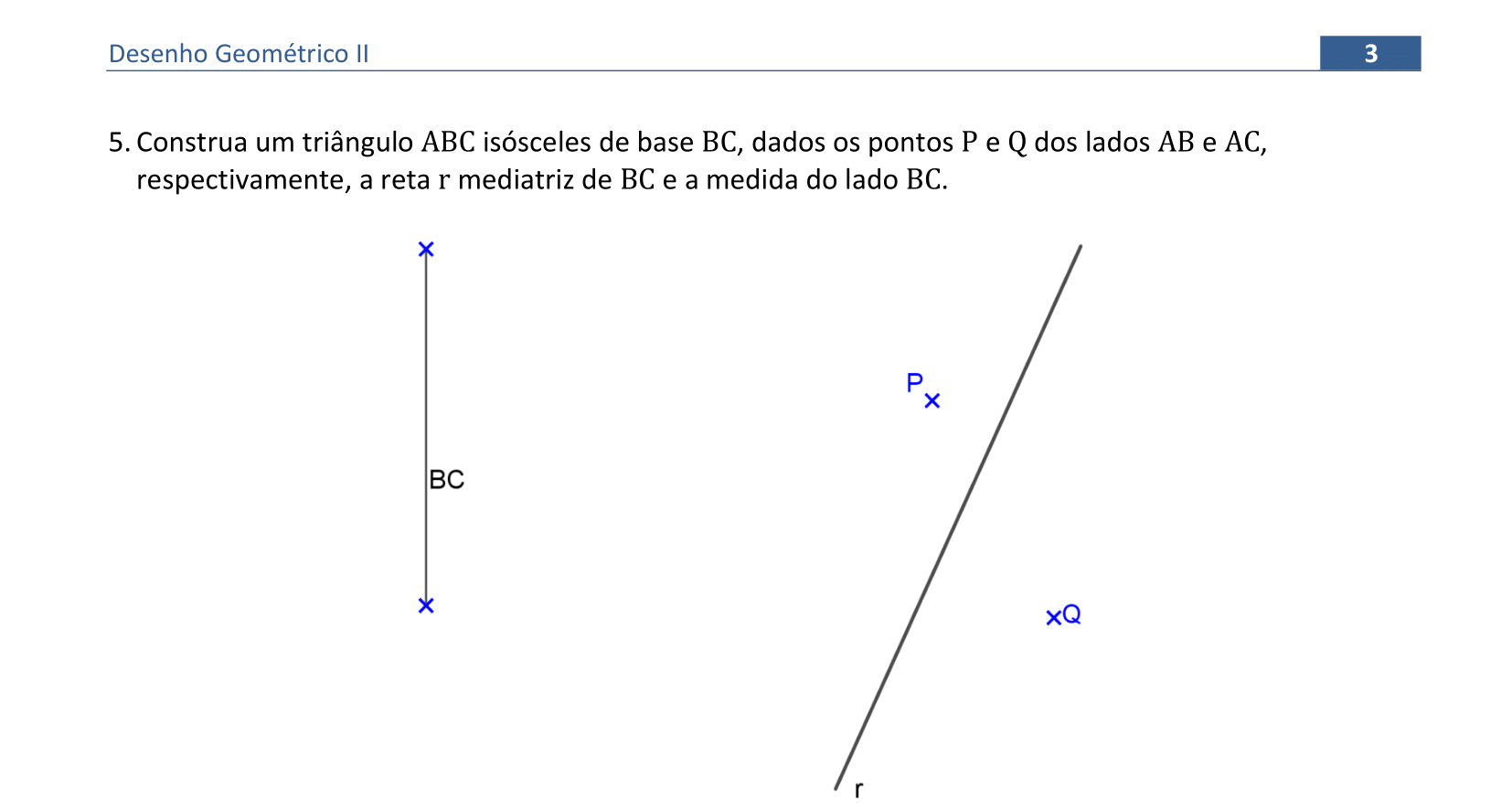
📏 📐 Resolução
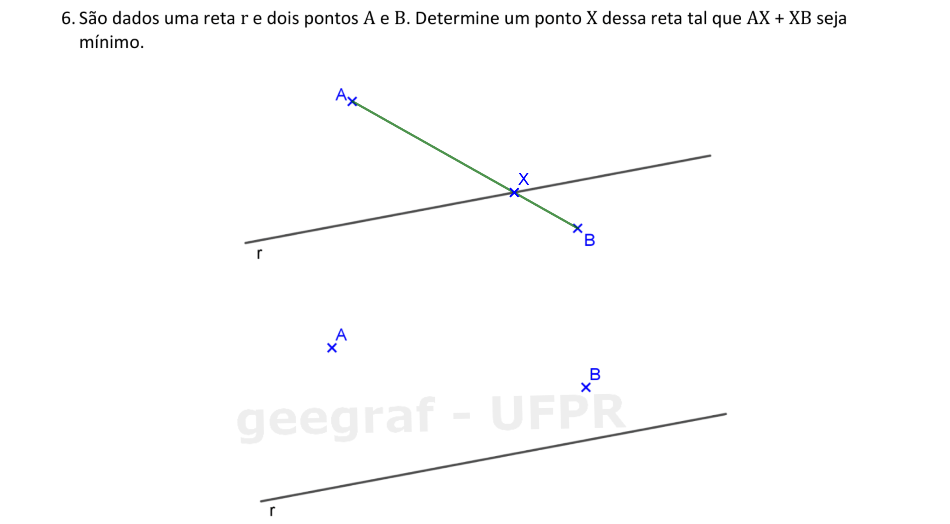
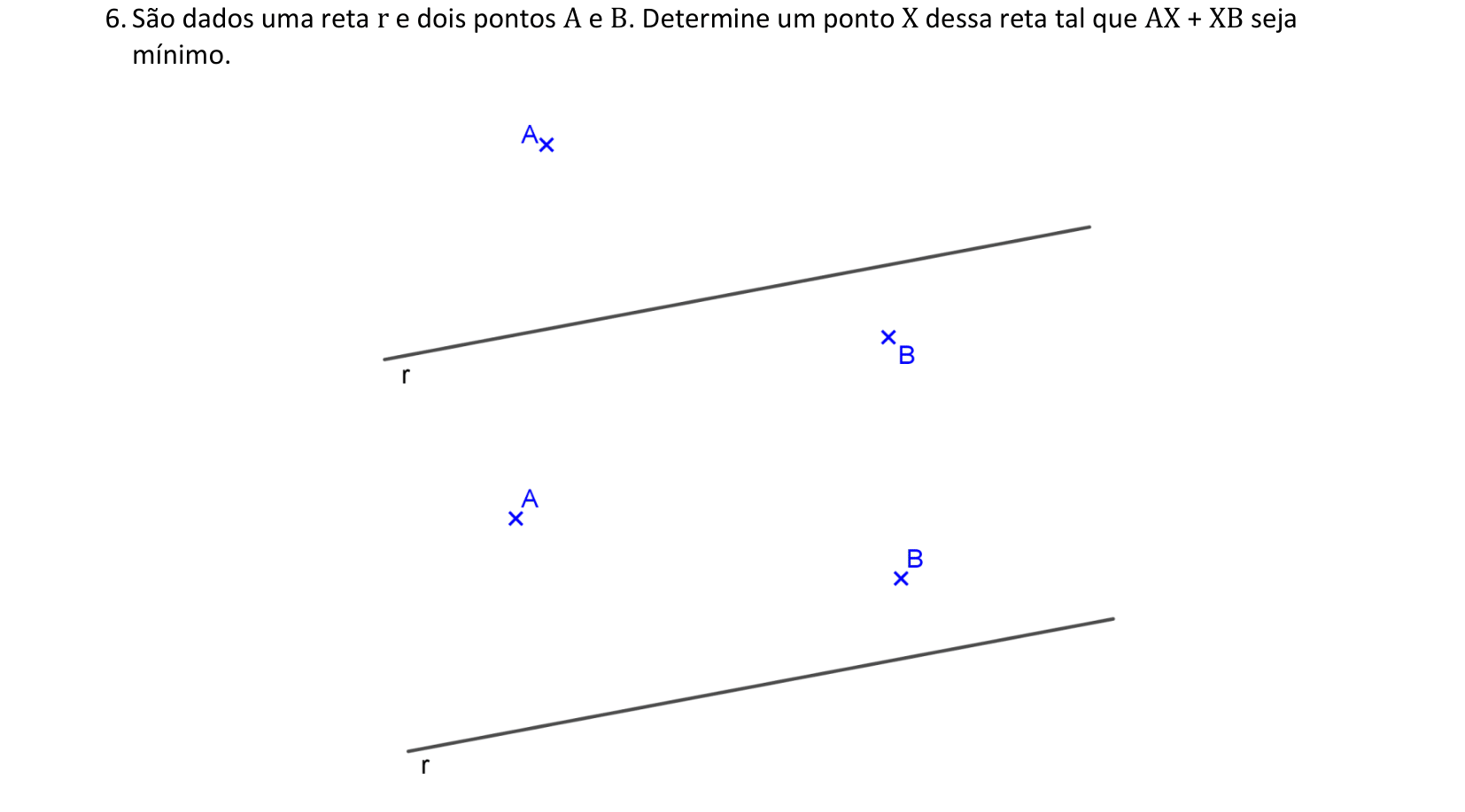
Neste problema, vamos usar o conceito da menor distância entre dois pontos de um plano.


📏 📐 Resolução
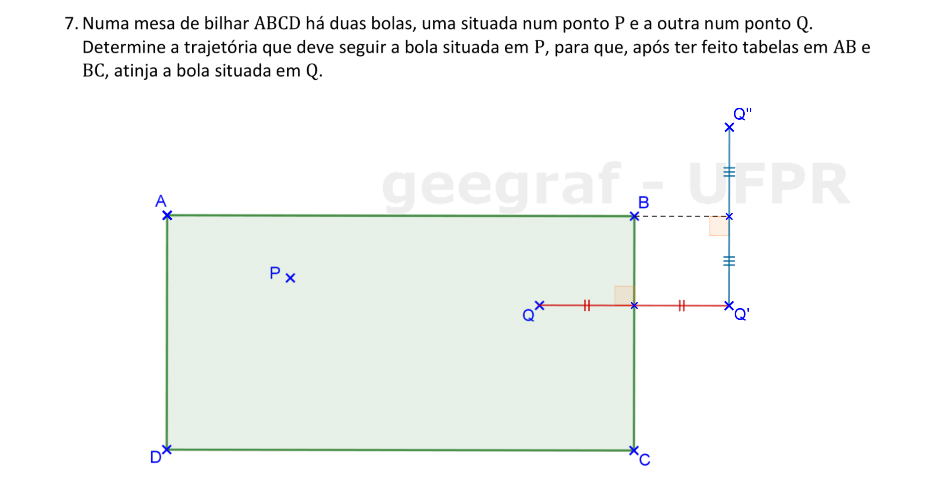
Neste problema, vamos usar o conceito dos ângulos de incidência e reflexão nas tabelas da mesa de bilhar.



📏 📐 Solução
Usando o conceito de distância mínima entre dois pontos, podemos encontrar os simétricos dos vértices A e B em relação aos lados do ângulo.
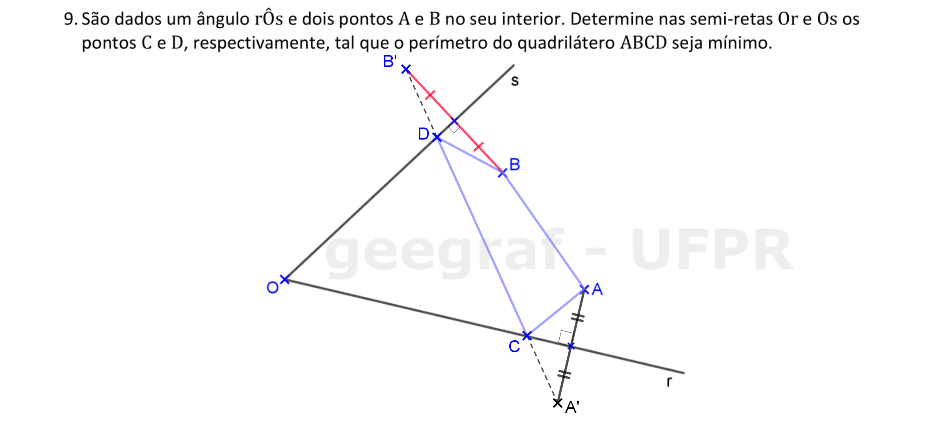

📏 📐 Solução
Usando o conceito de distância mínima entre dois pontos, podemos encontrar os simétricos do vértice A em relação aos lados do ângulo.


📏 📐 Solução
Usando o conceito de ângulos de incidência e reflexão, podemos encontrar os simétricos do foco F e do objeto O em relação aos espelhos planos r e s.

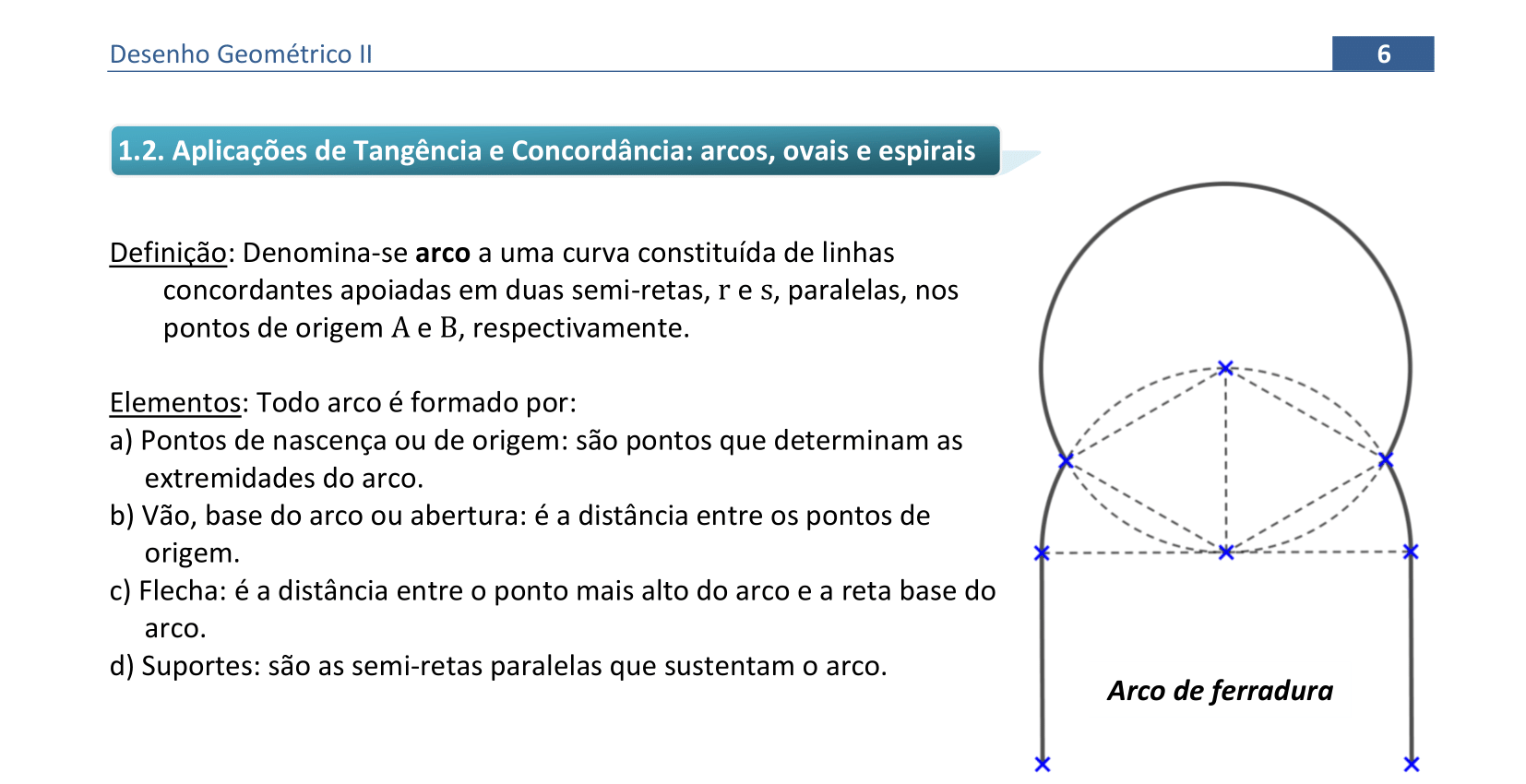
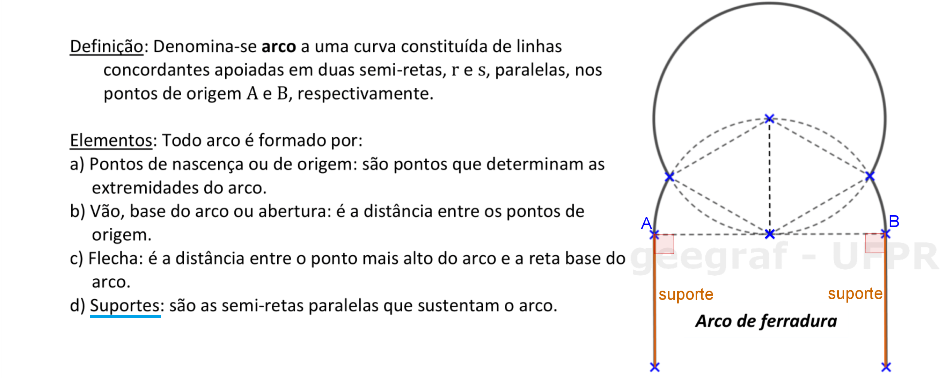
📑 Propriedades
Considere o arco de ferradura mostrado nesta página. Vamos analisar quais são os elementos de um arco arquitetônico.
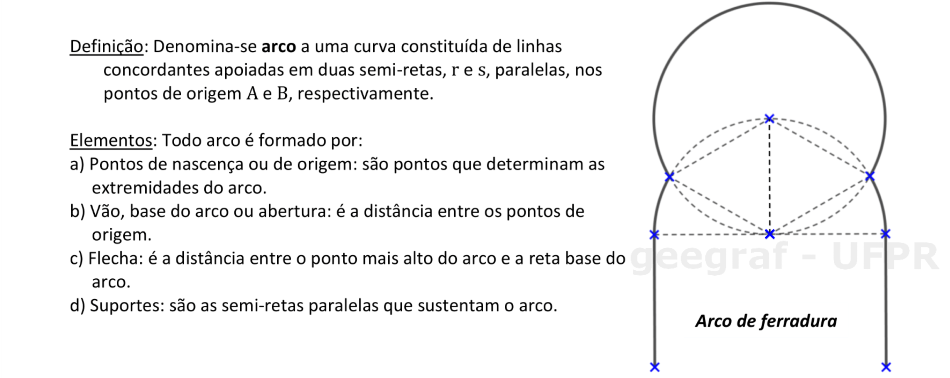

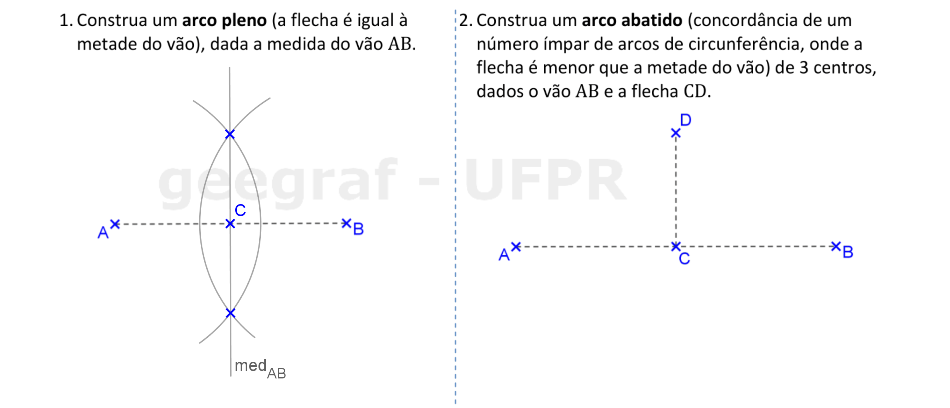
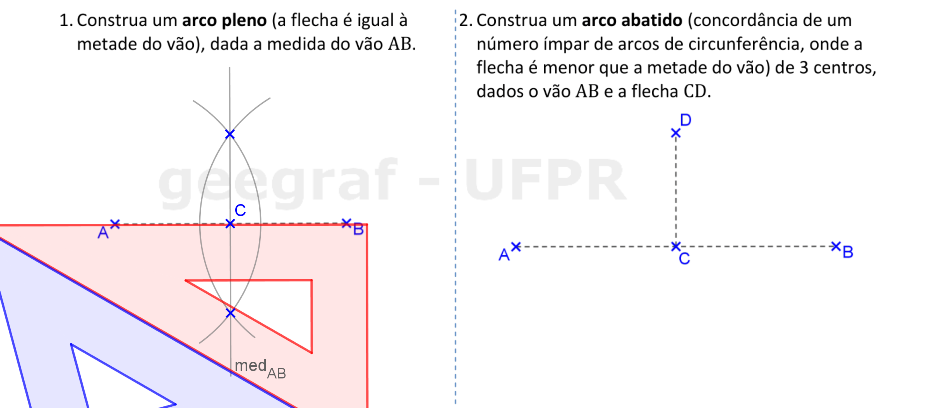
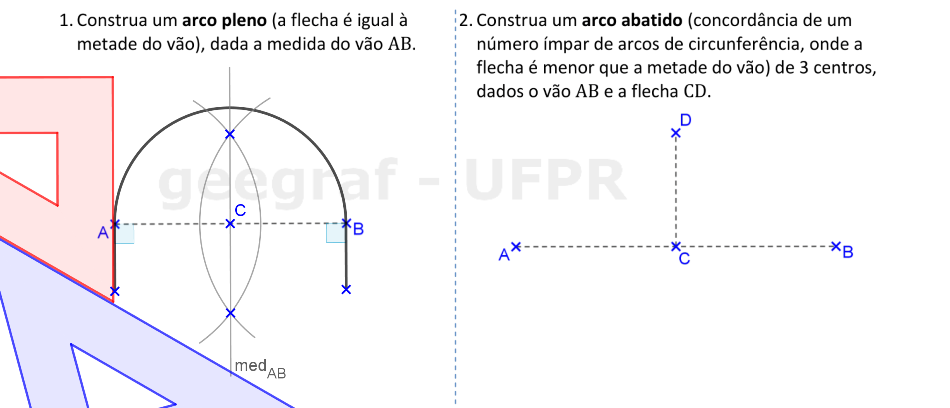
📏 📐 Resolução: 1ª parte
O arco pleno tem o centro na metade do vão.

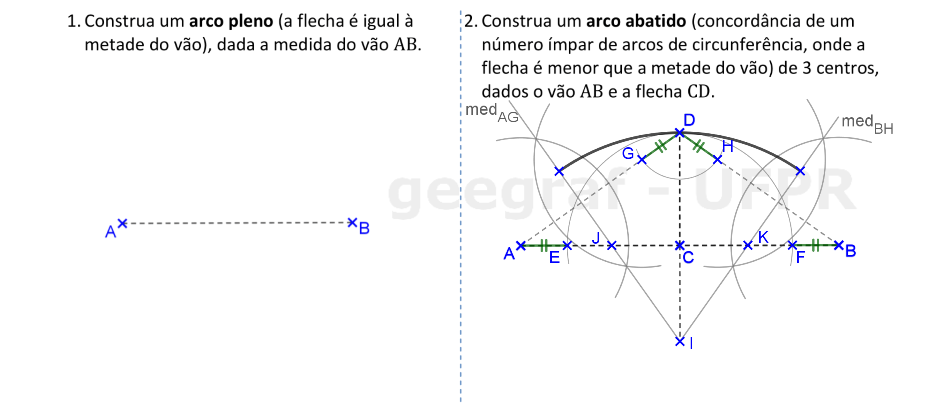
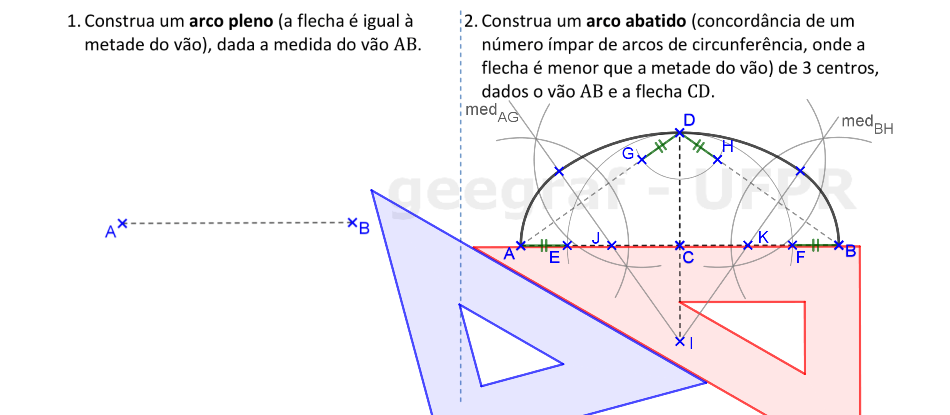
📏 📐 Resolução: 2ª parte
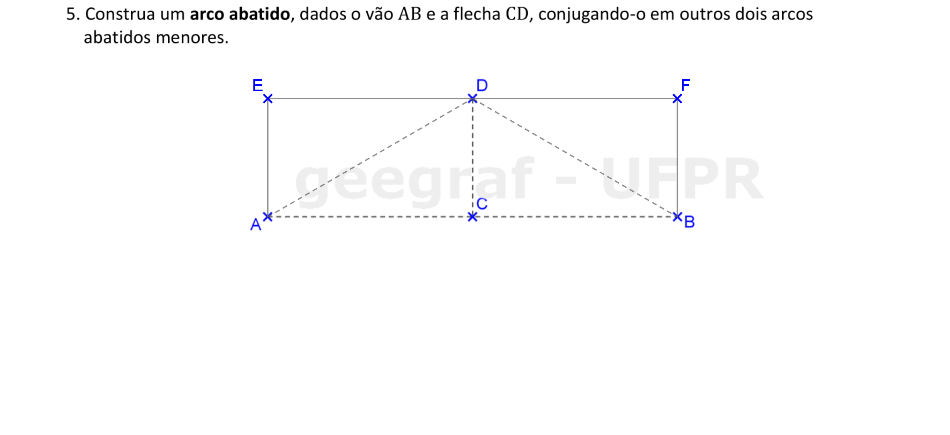
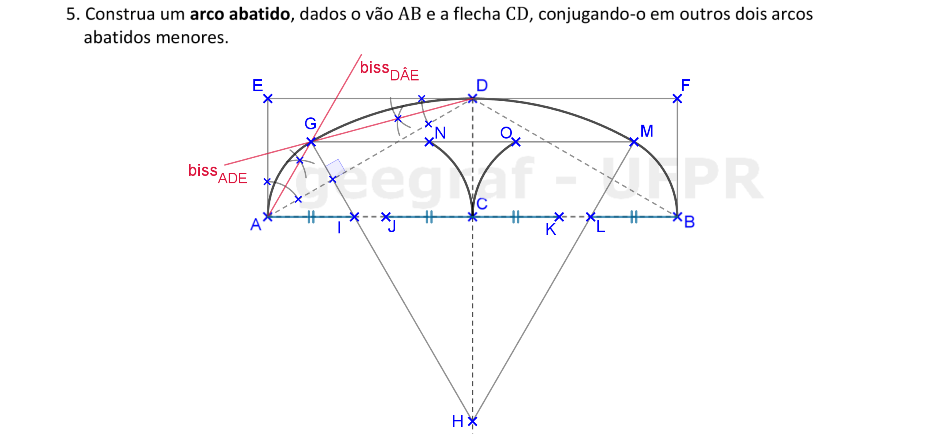
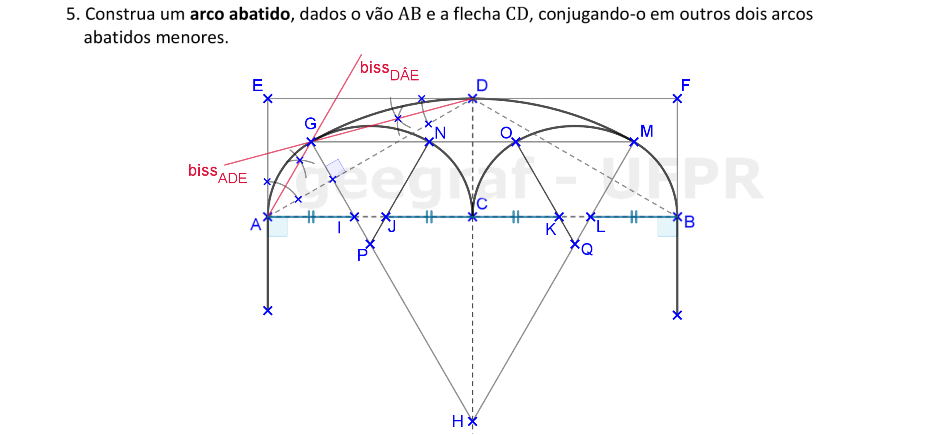
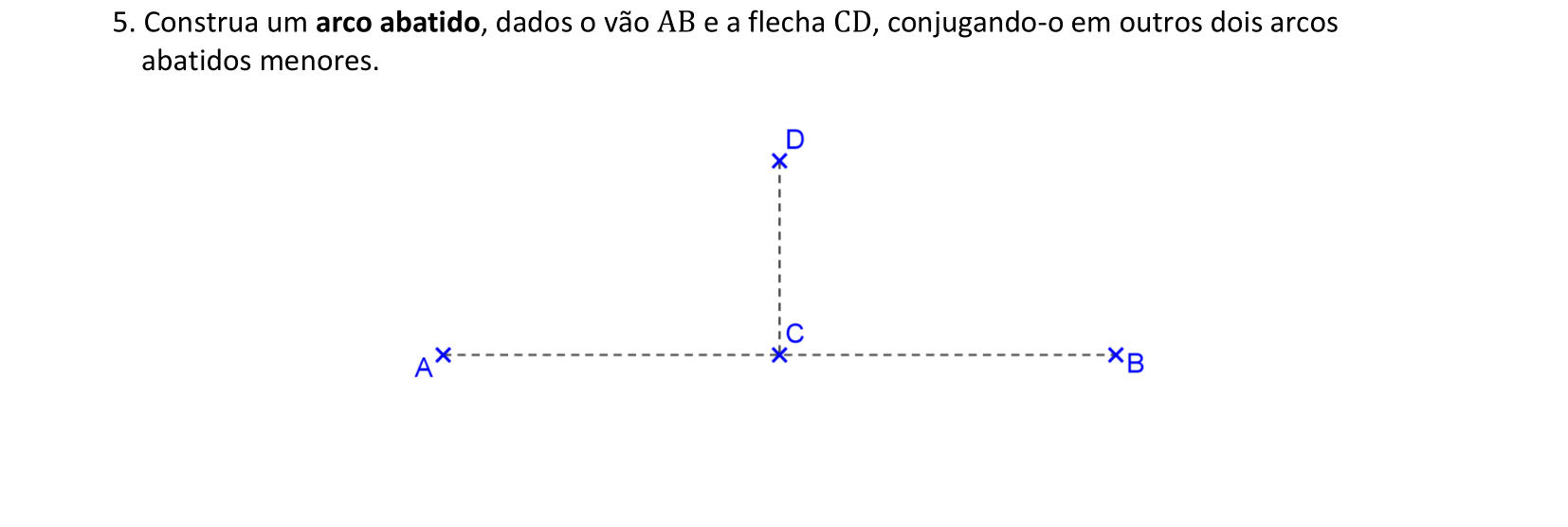
Agora vamos construir o arco abatido, com o uso de 3 centros. A flecha está definida pelo segmento CD, que contém o ponto mais alto deste arco.



📏 📐 Solução
Quando a medida da flecha não for considerada, podemos definir a mediatriz do vão AB como eixo de simetria e escolher um centro E qualquer da mediatriz.

📏 📐 Resolução
Vamos começar construindo os centros do arco maior com um retângulo de lados iguais ao vão AB e a flecha CD.


📏 📐 Resolução
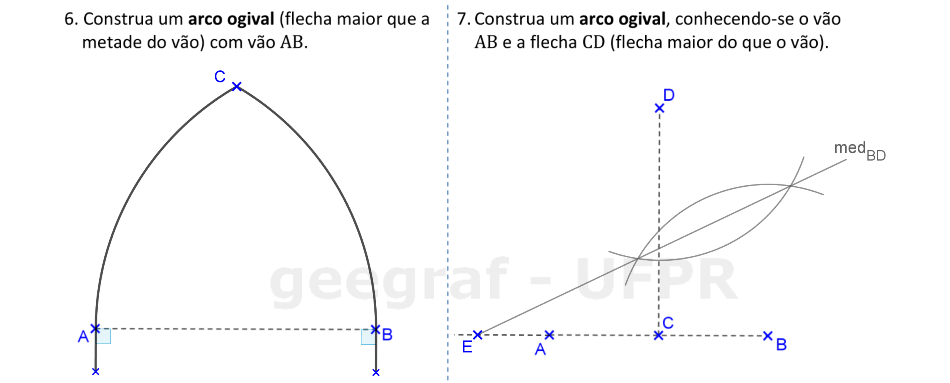
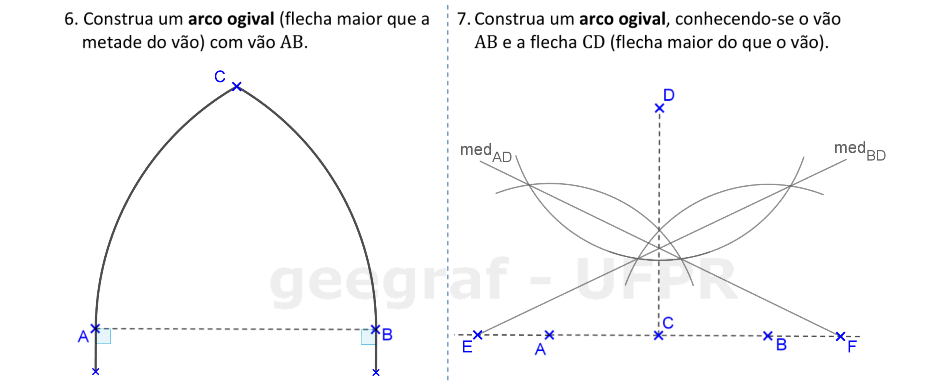
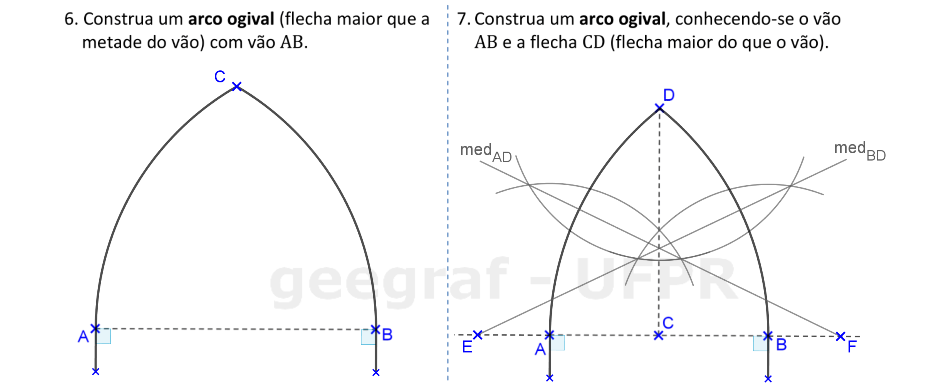
Vamos construir o arco ogival de duas formas: considerando a flecha com tamanho fixo e com a flecha dependente da medida do vão AB.


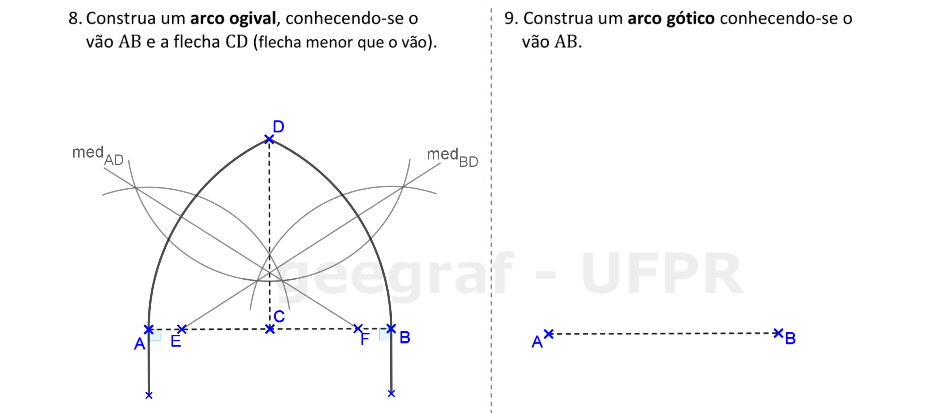
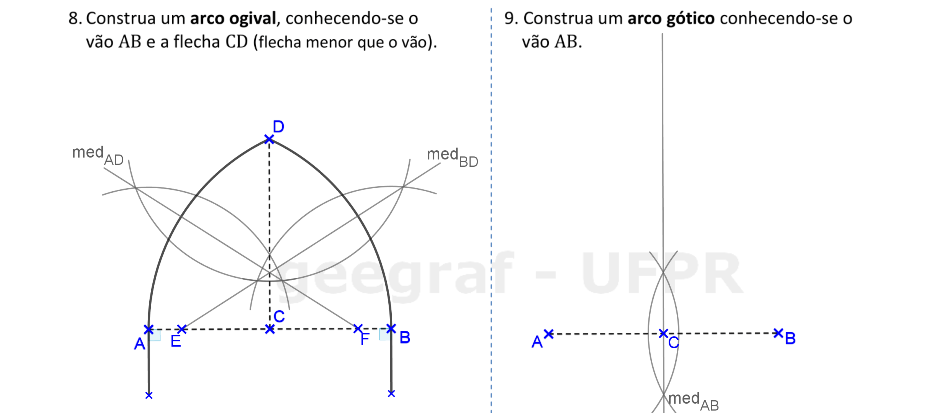
📏 📐 Resolução
Vamos construir um arco ogival com a flecha com tamanho menor do que o vão e um arco gótico.


📏 📐 Resolução
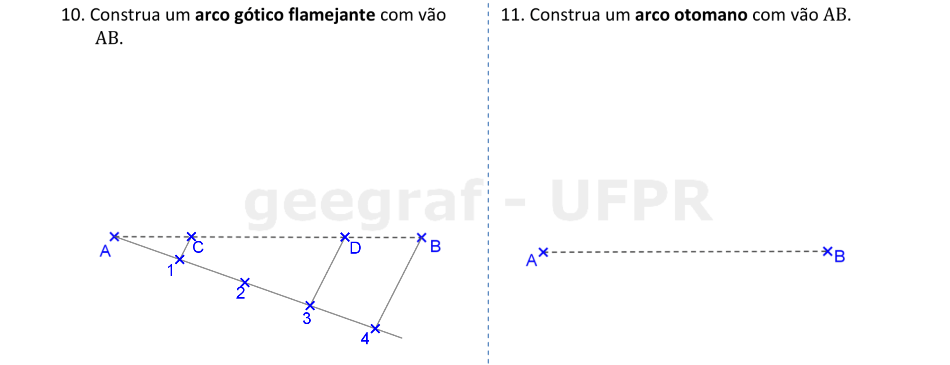
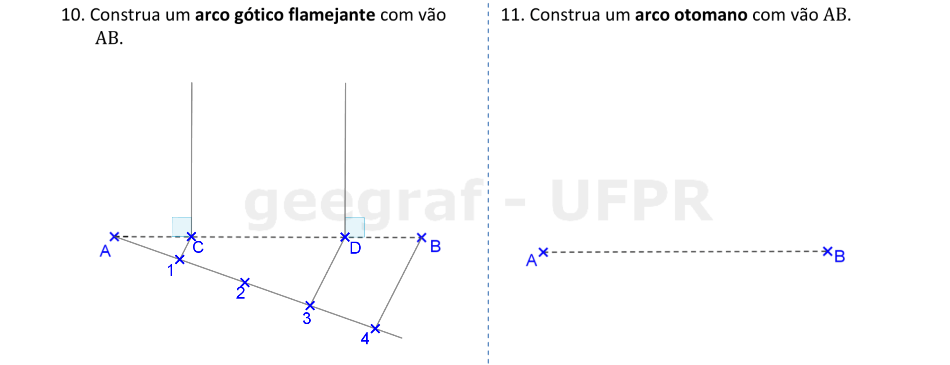
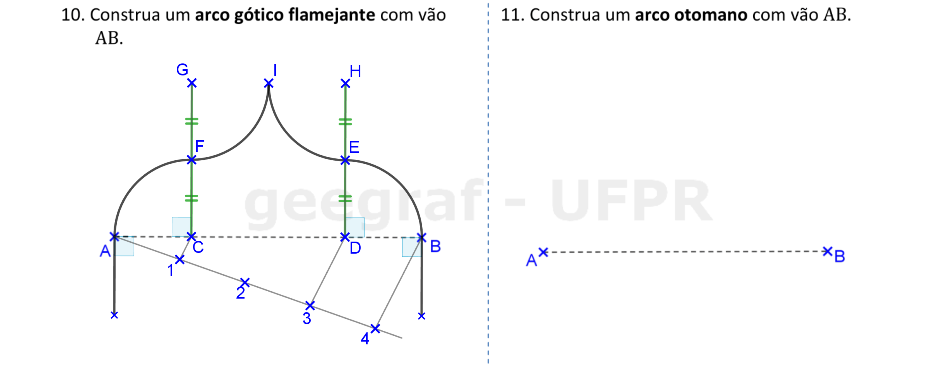
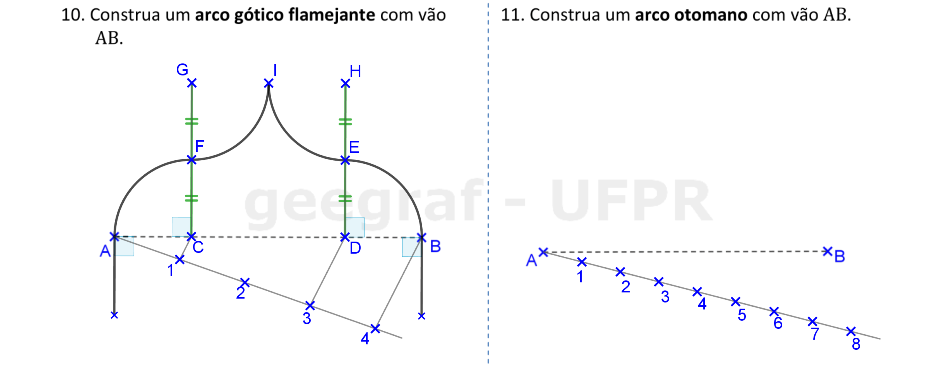
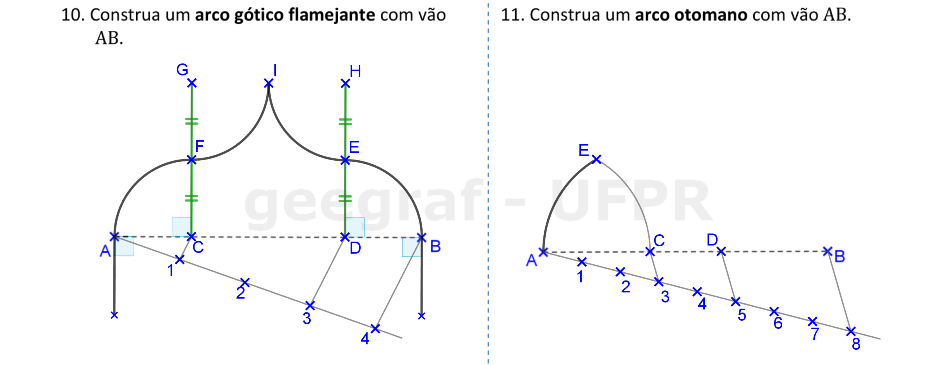
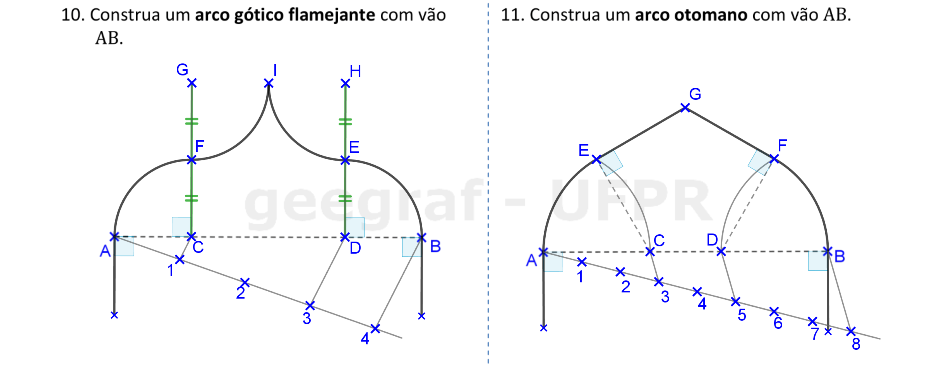
Vamos construir os arcos gótico flamejante e otomano.


📏 📐 Resolução
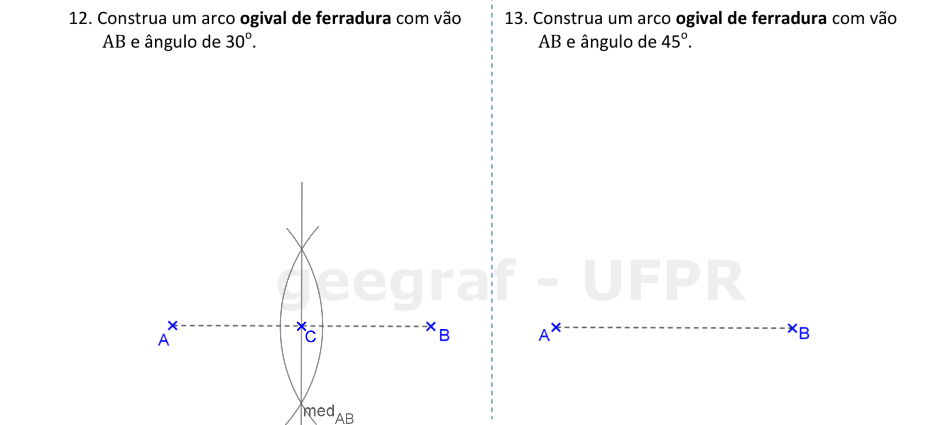
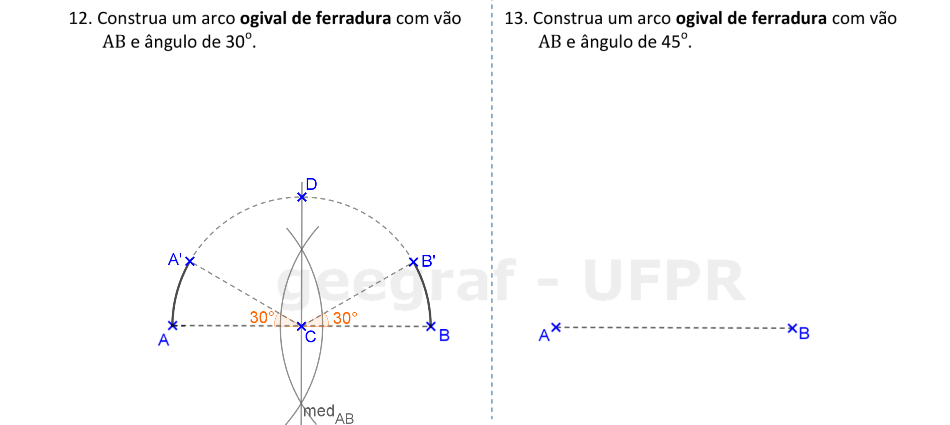
Vamos construir os arcos ogivais de ferradura com ângulos centrais de 30° e 45°.


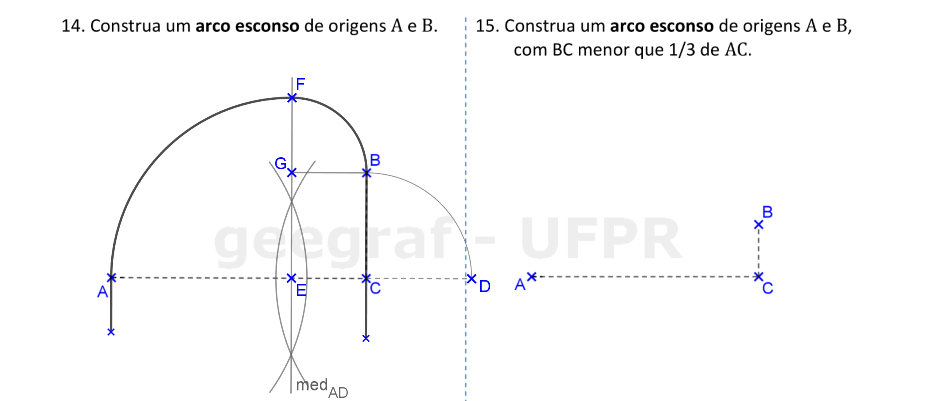
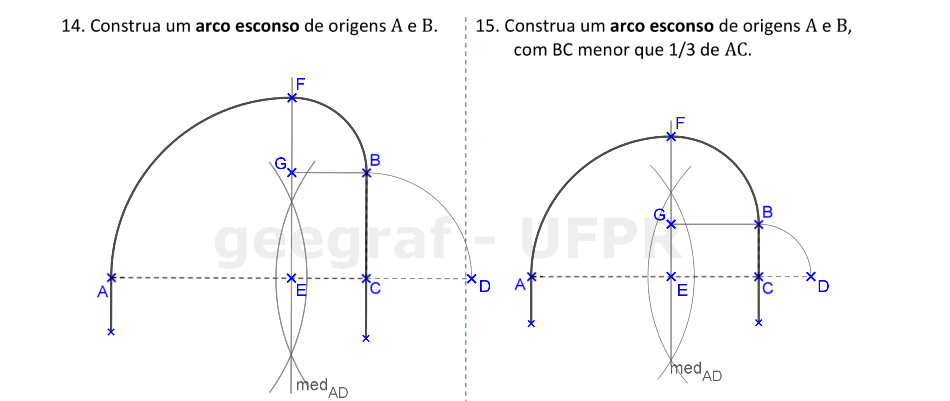
📏 📐 Resolução
Vamos construir os arcos assimétricos denominados esconsos.
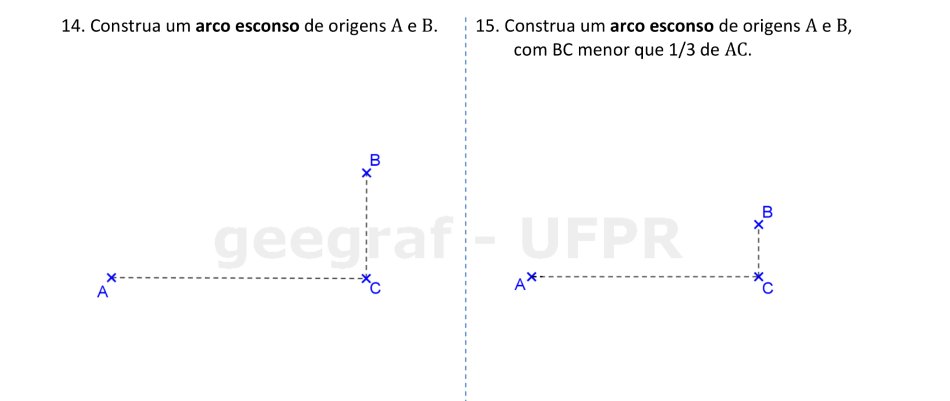

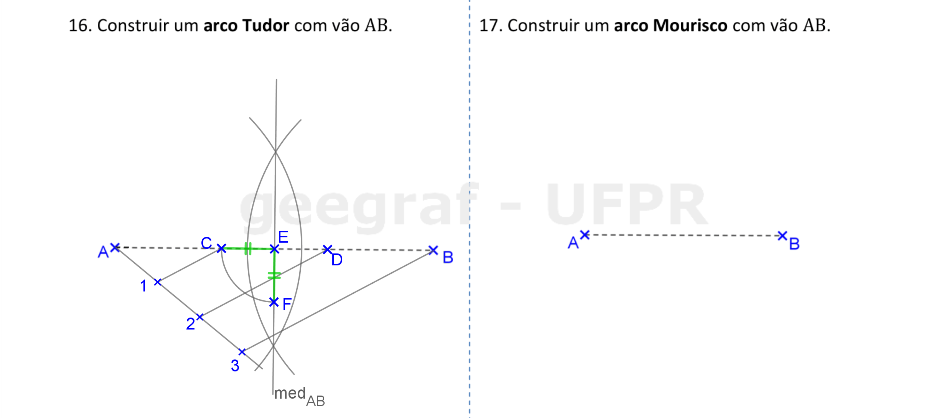
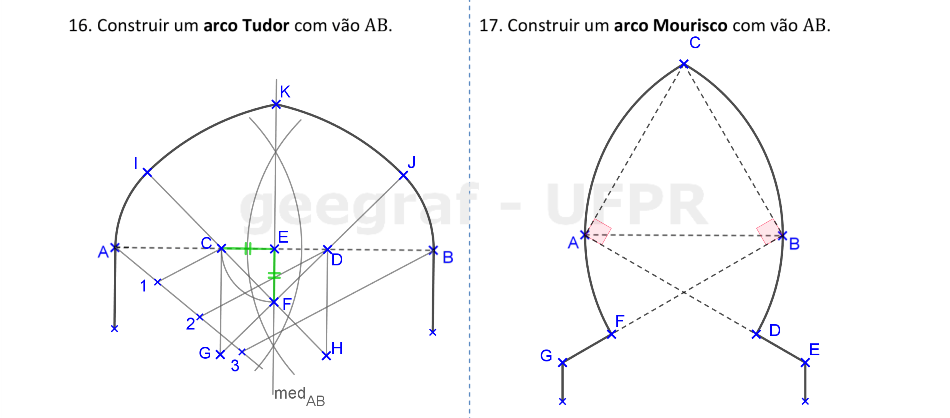
📏 📐 Resolução
Vamos construir os arcos Tudor e Mourisco.


📏 📐 Resolução
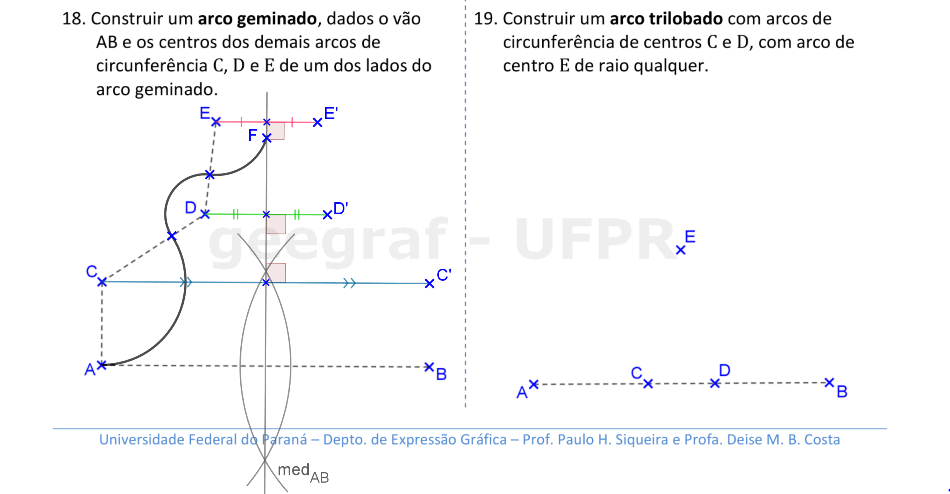
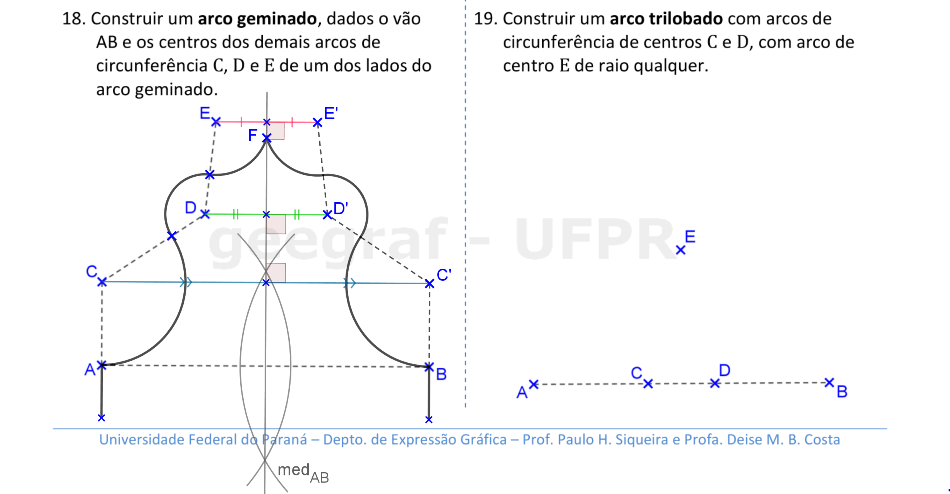
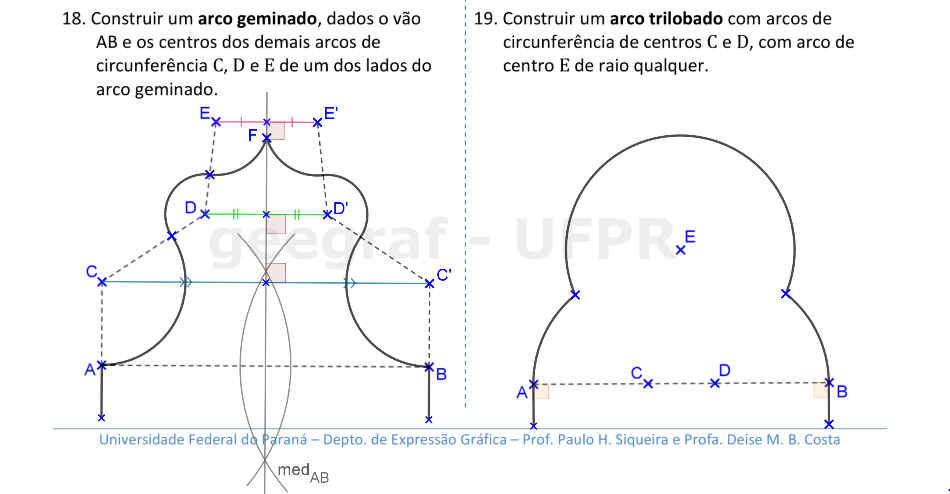
Vamos construir os arcos geminado e trilobado.


📏 📐 Resolução
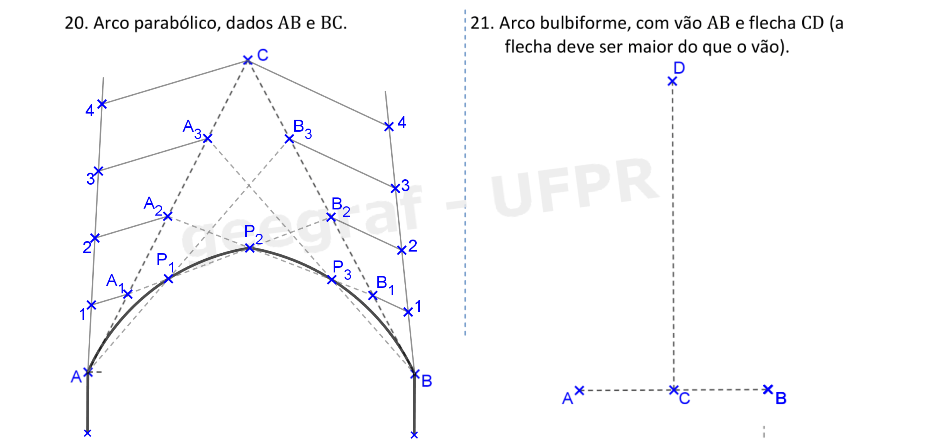
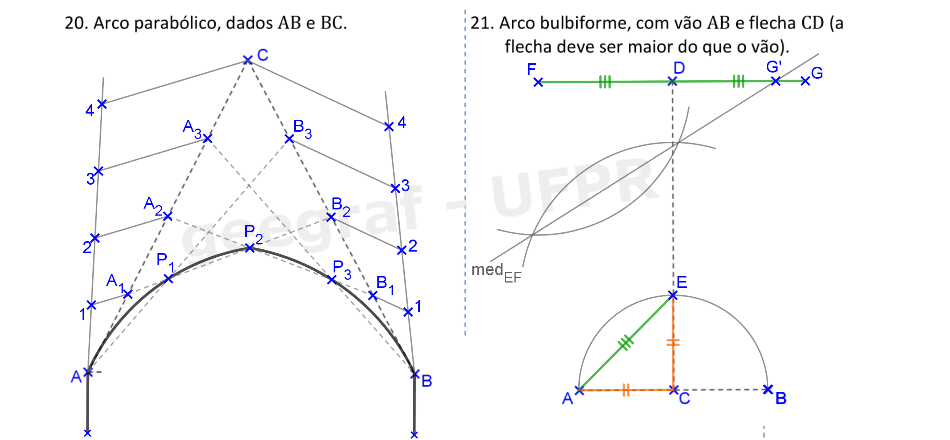
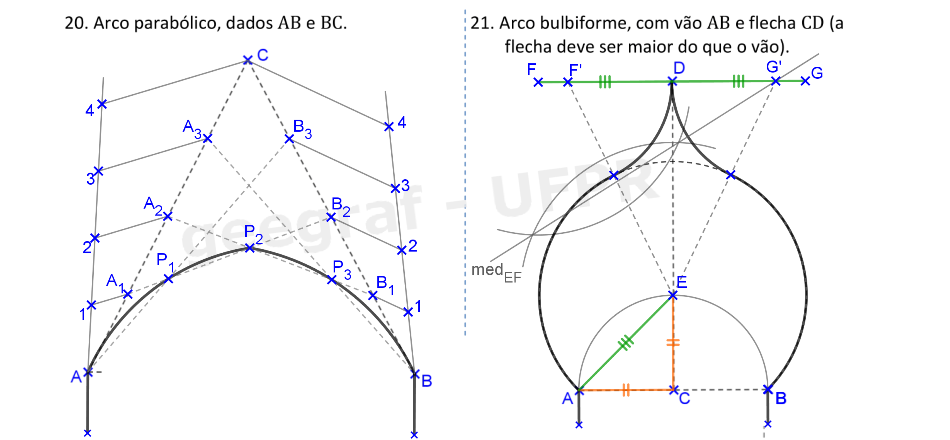
Vamos construir os arcos parabólico e bulbiforme.


📑 Propriedades
Vamos acompanhar algumas definições de elementos das curvas chamadas ovais ou falsas elipses.


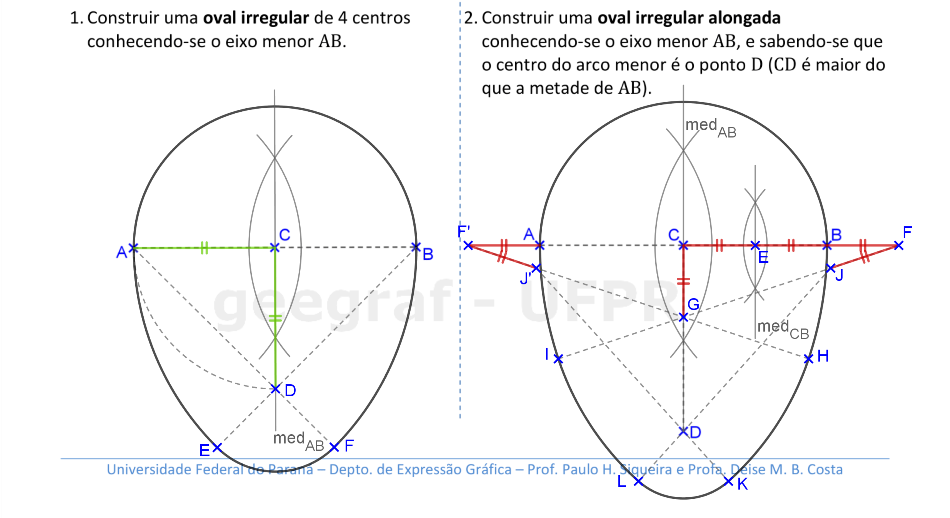
📏 📐 Resolução
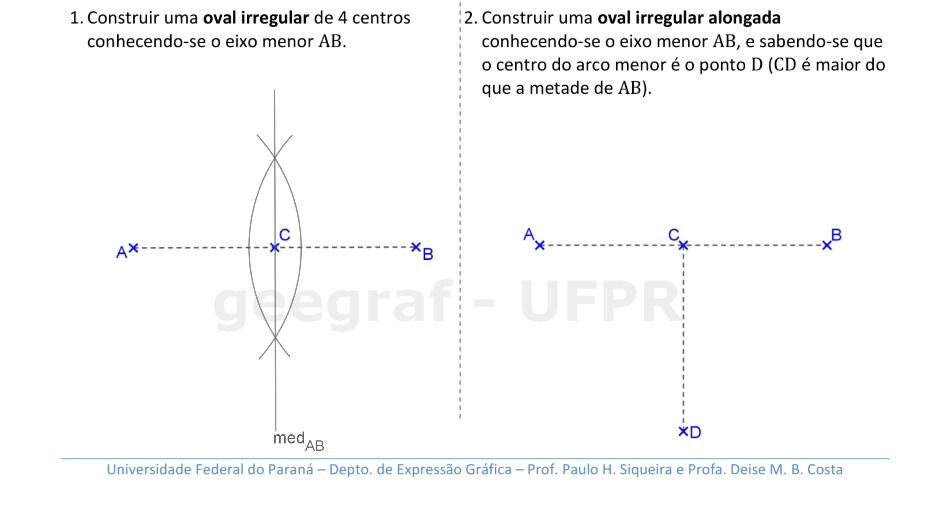
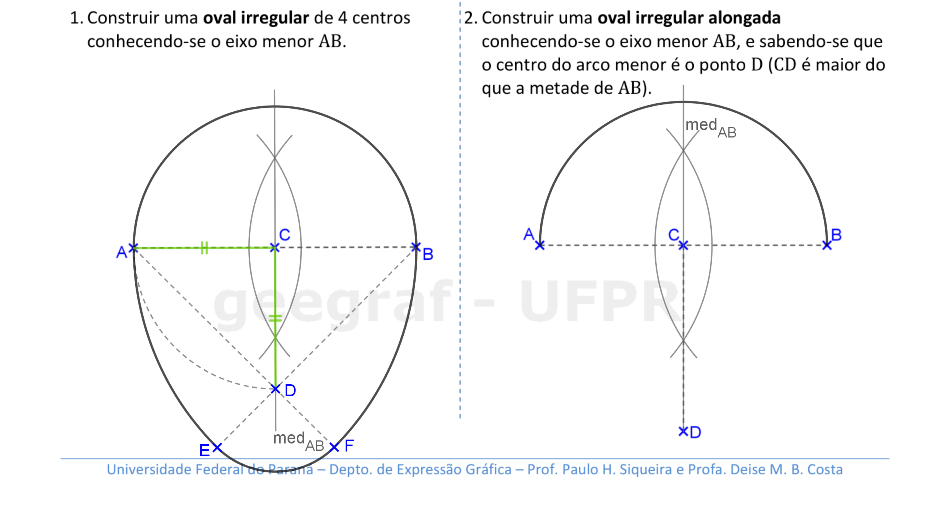
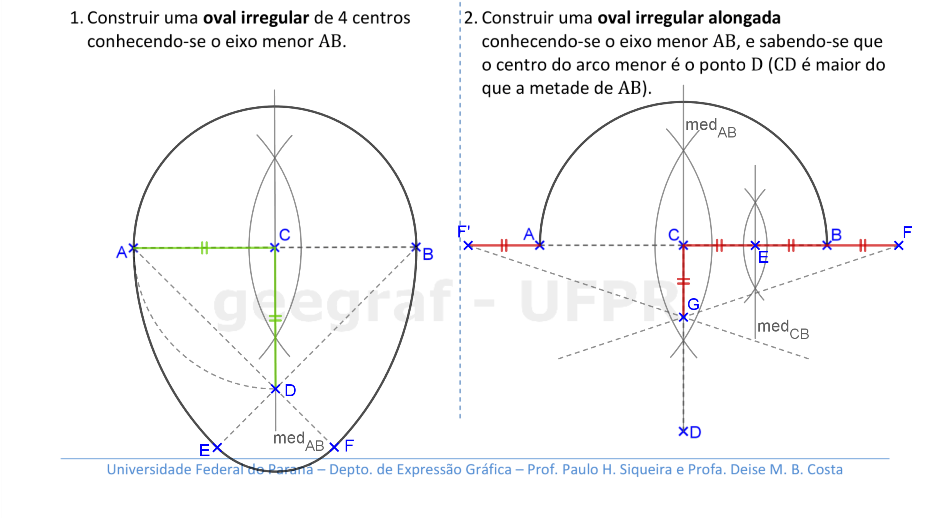
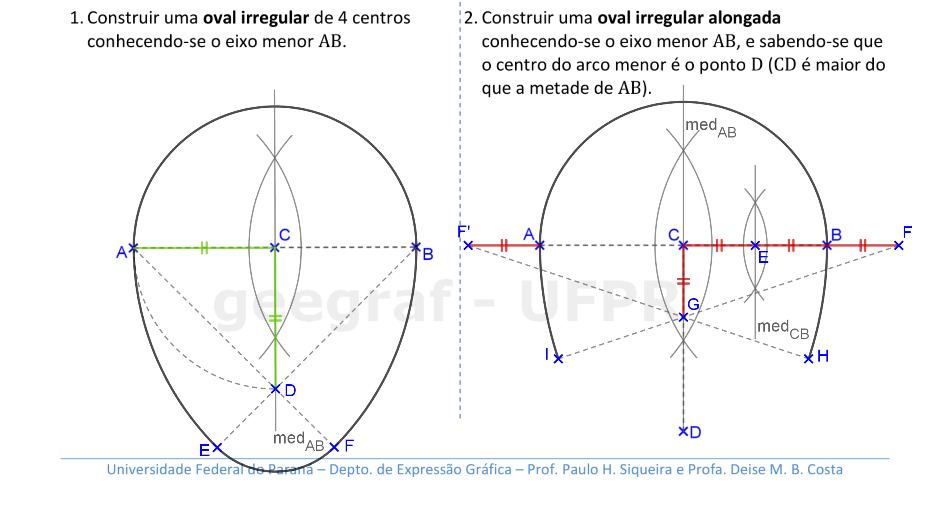
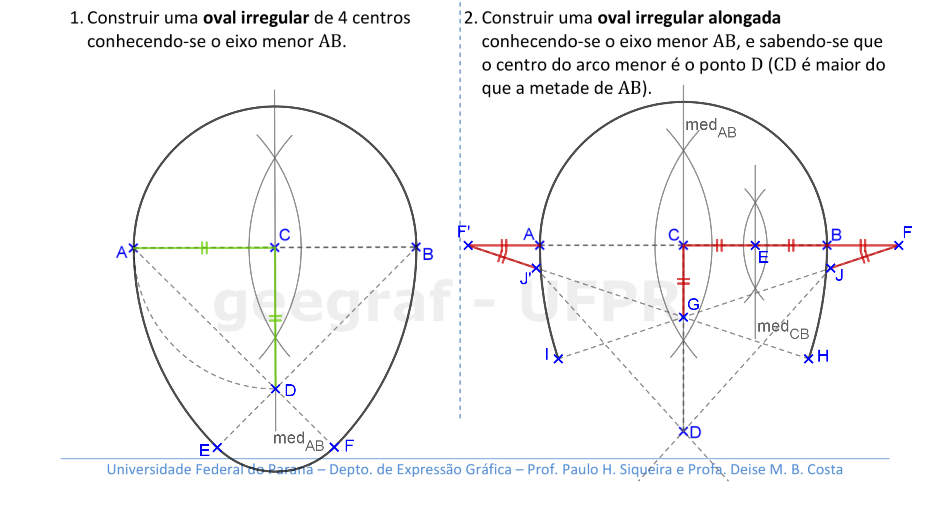
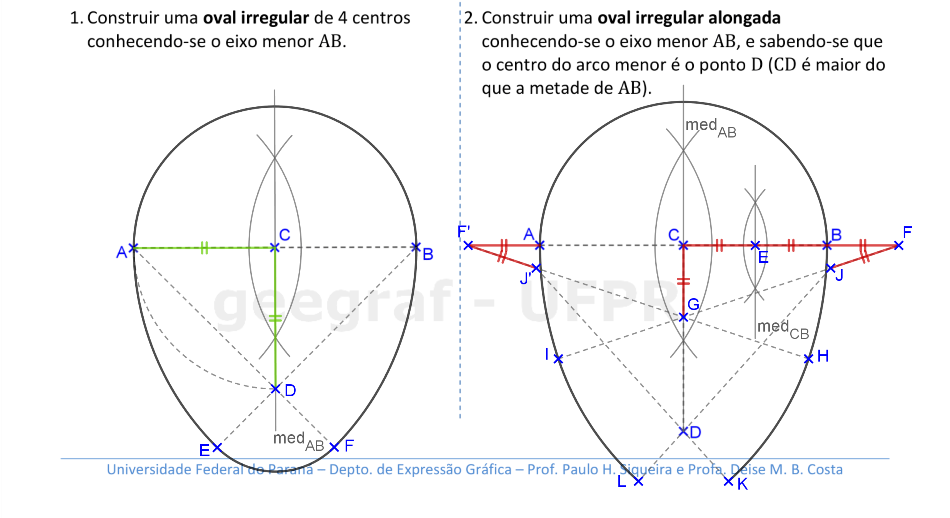
Vamos construir ovais irregulares. Nestes casos, temos apenas um eixo de simetria nestas curvas.

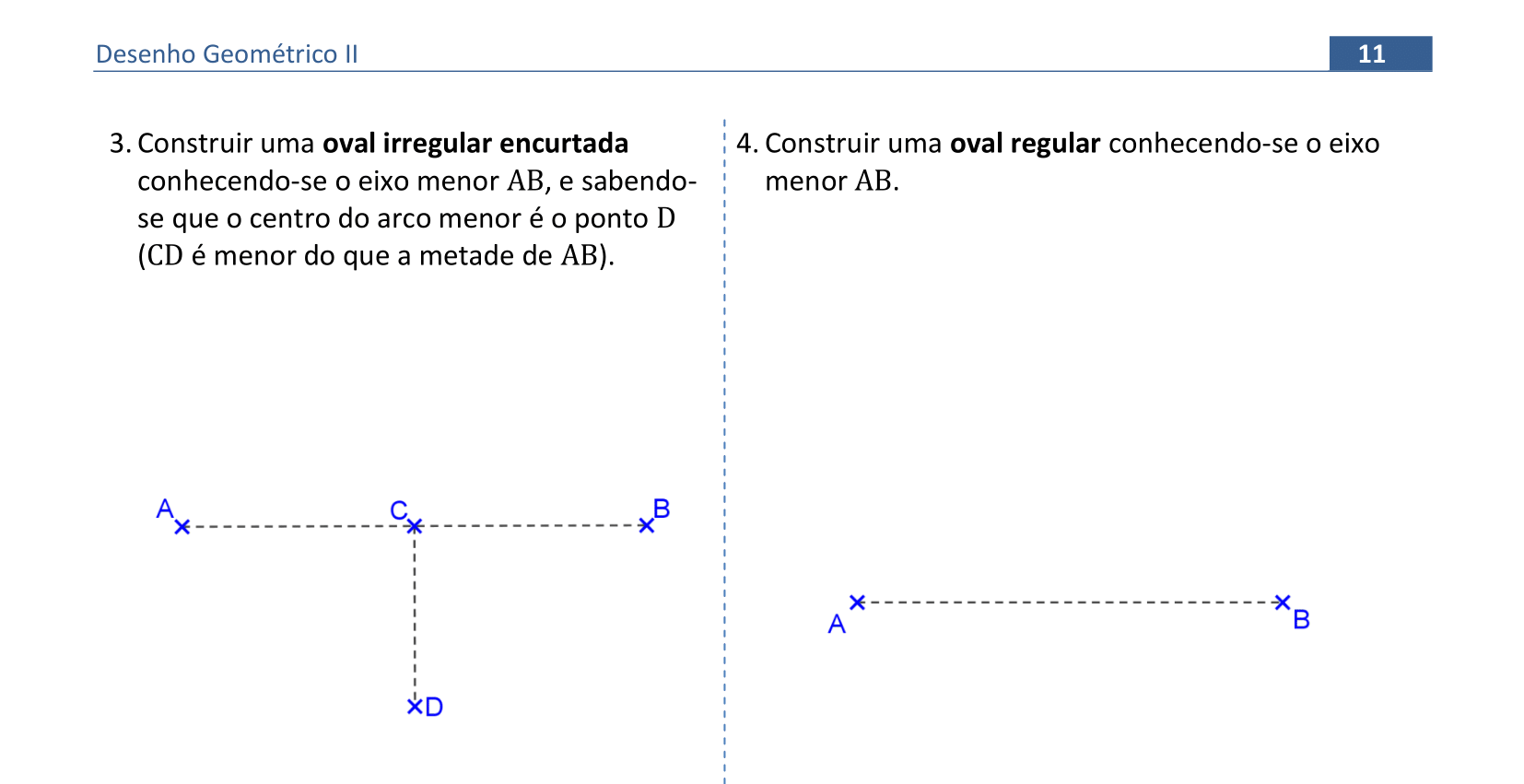
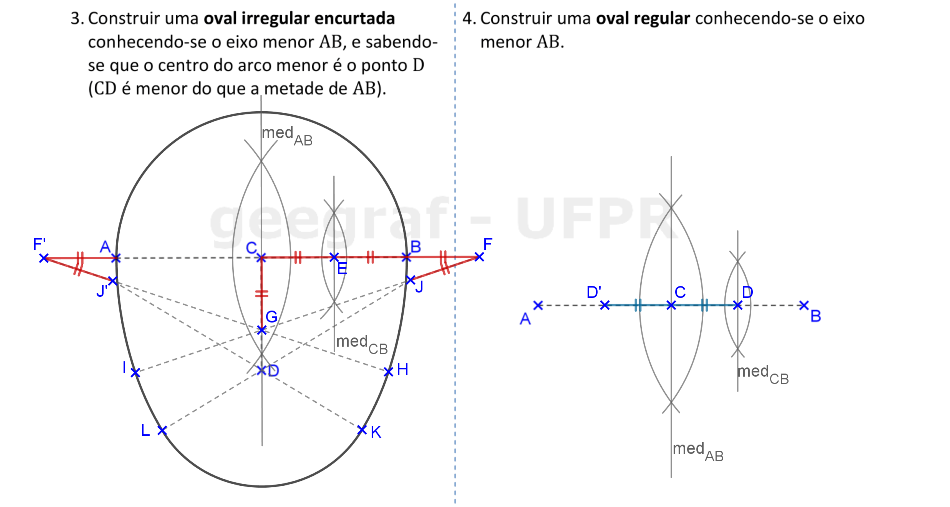
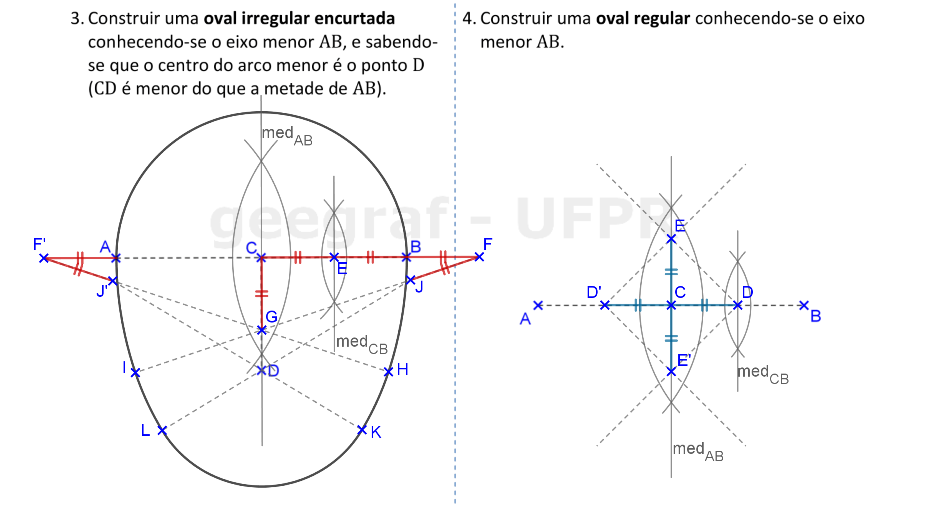
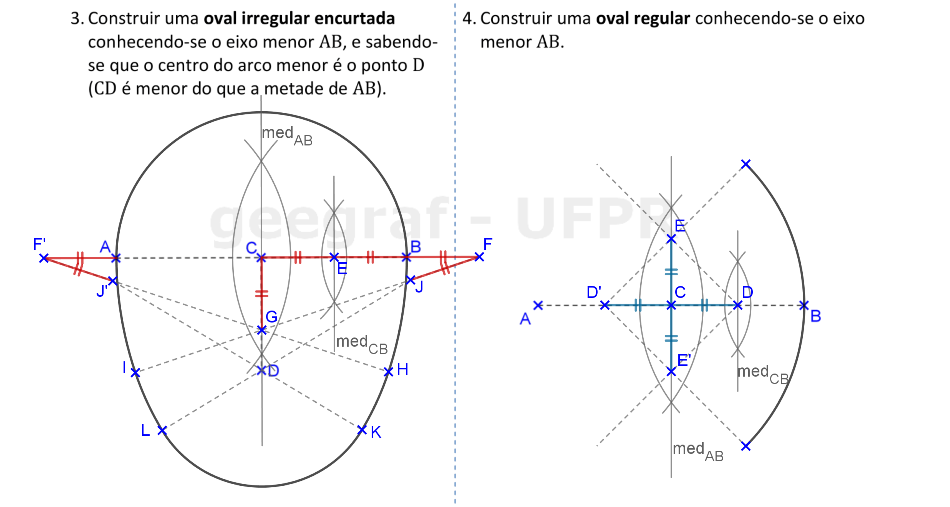
📏 📐 Resolução
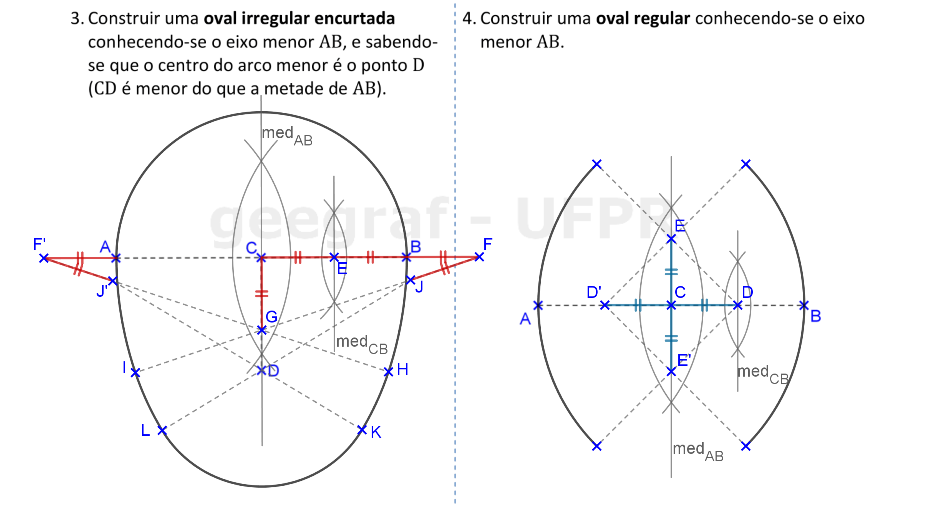
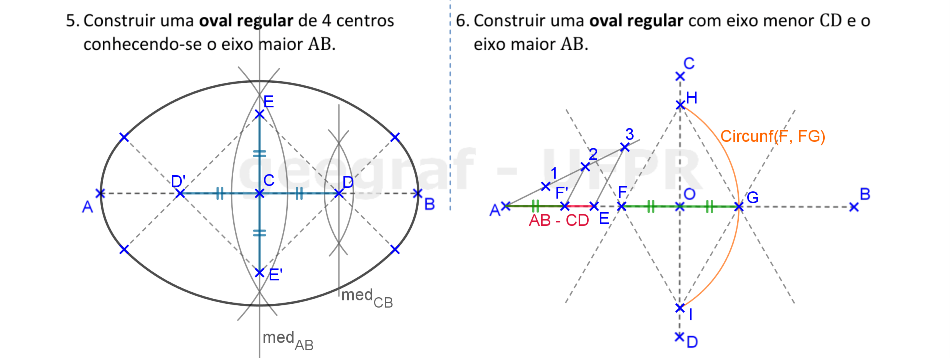
Vamos construir uma oval irregular encurtada e uma oval regular. Os diâmetros das ovais regulares são eixos de simetria das curvas.


📏 📐 Resolução
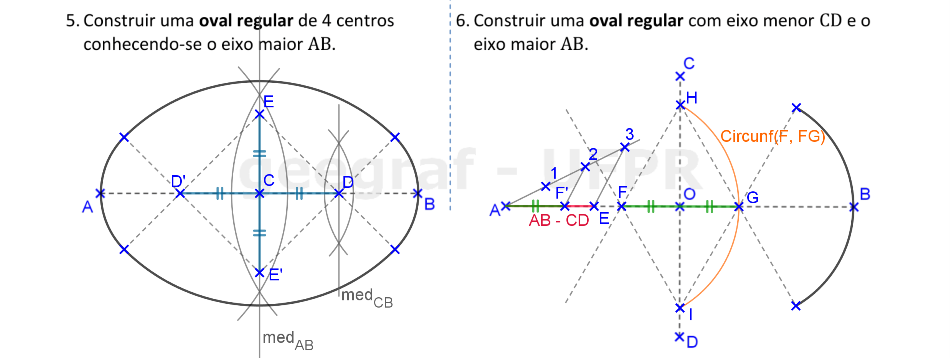
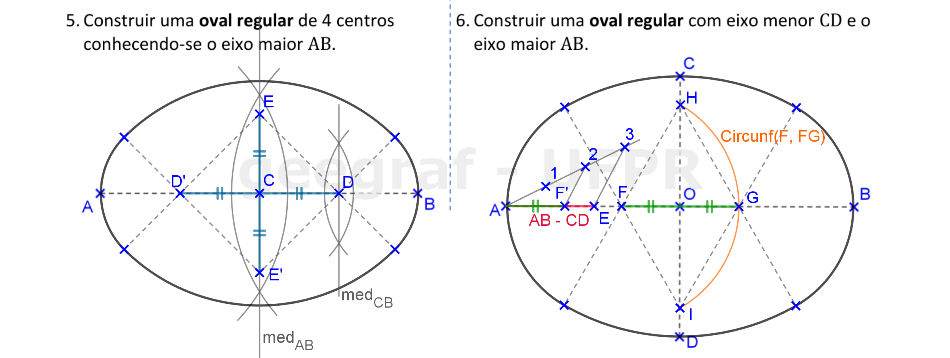
Vamos construir ovais regulares: uma com apenas a medida do eixo maior e a outra com as medidas dos dois eixos.


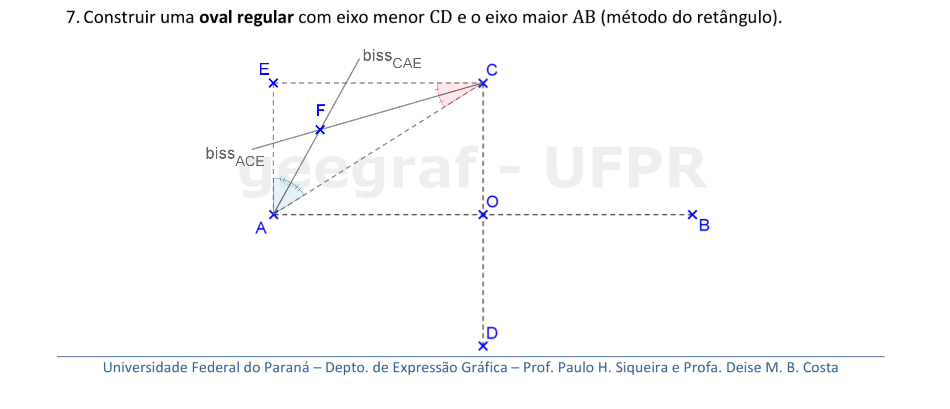
📏 📐 Resolução
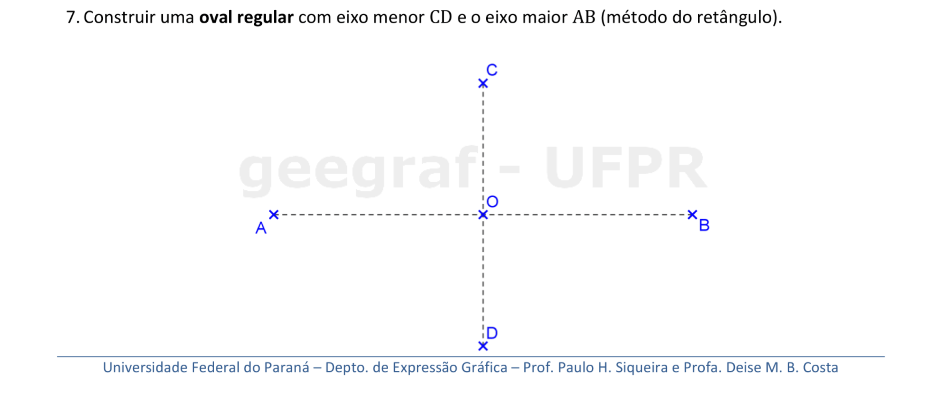
Vamos construir uma oval com as medidas dos dois eixos dadas. O método do retângulo foi usado para construirmos um arco abatido.
2. Espirais e elipses
Material da página 12 até a página 25.
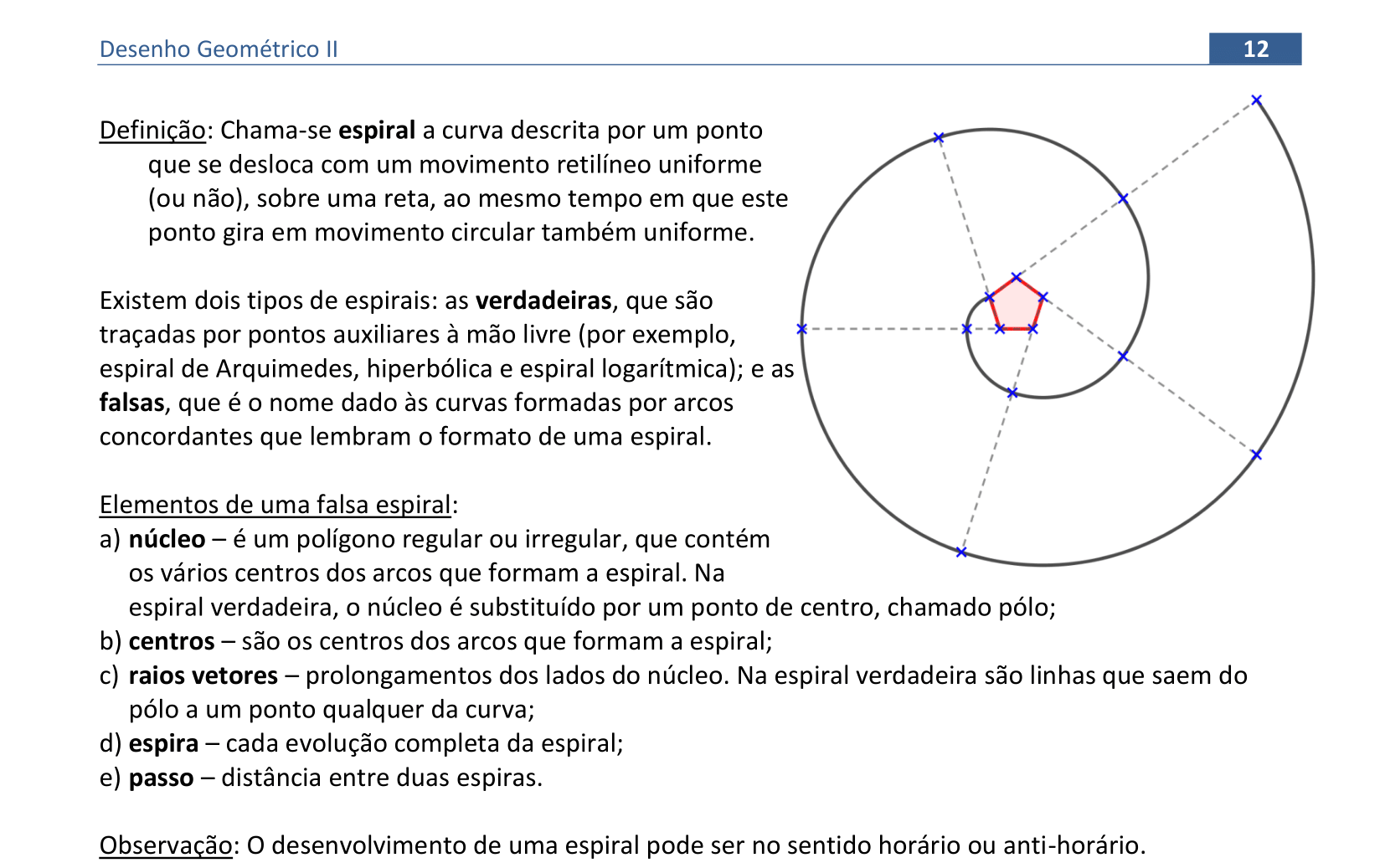
📑 Propriedades
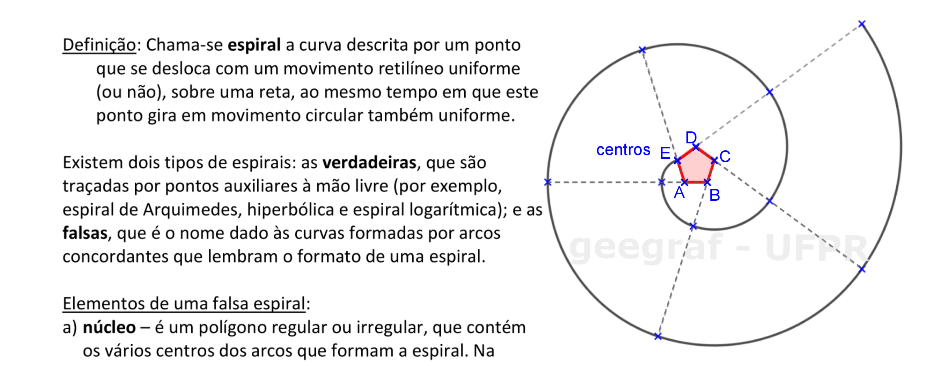
Veremos agora as definições usadas nas construções das espirais. Estas curvas podem ser construídas por pontos auxiliares e construídas à mão livre, ou construídas com arcos de concordâncias.


📏 📐 Resolução
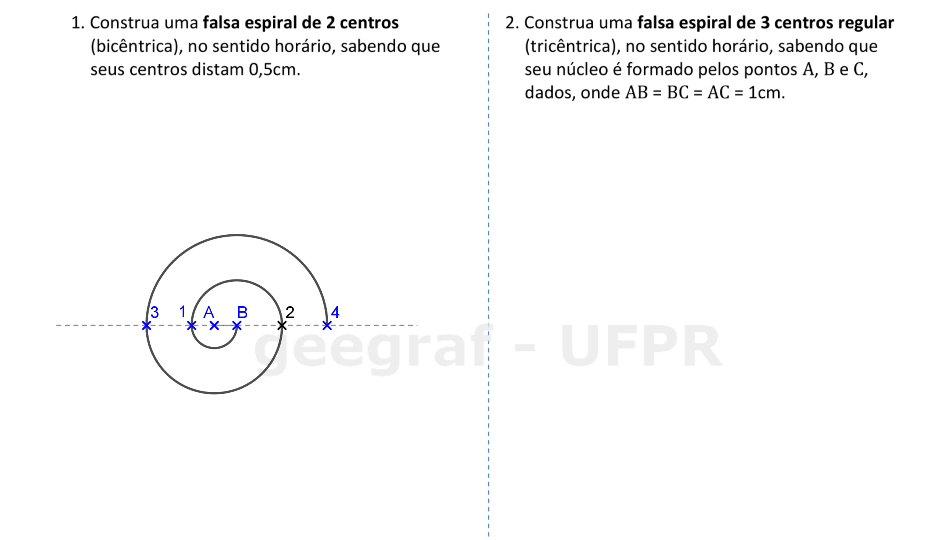
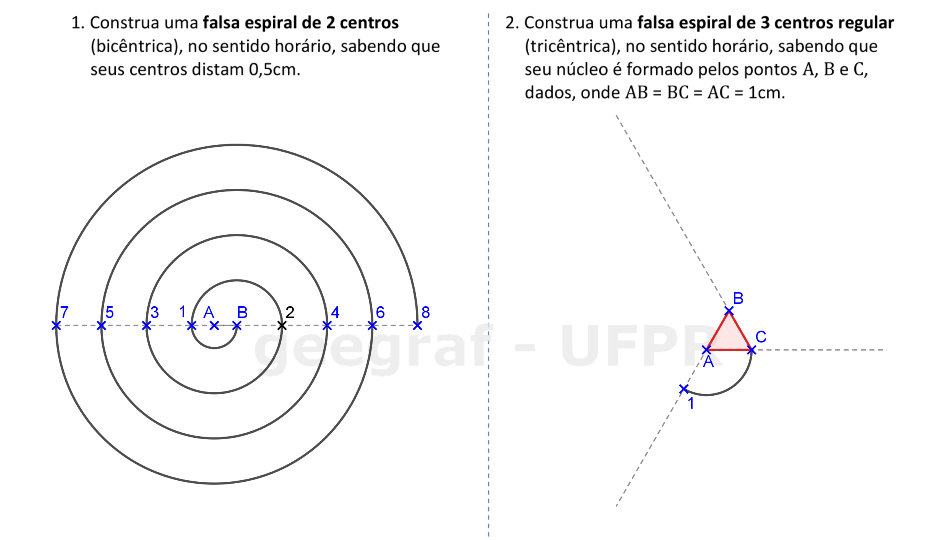
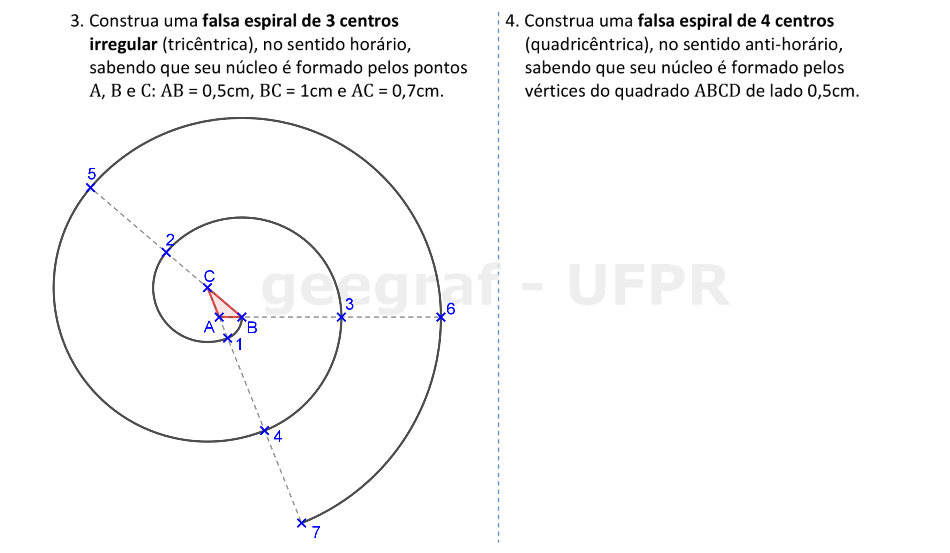
Vamos construir falsas espirais com 2 e com 3 centros.


📏 📐 Resolução
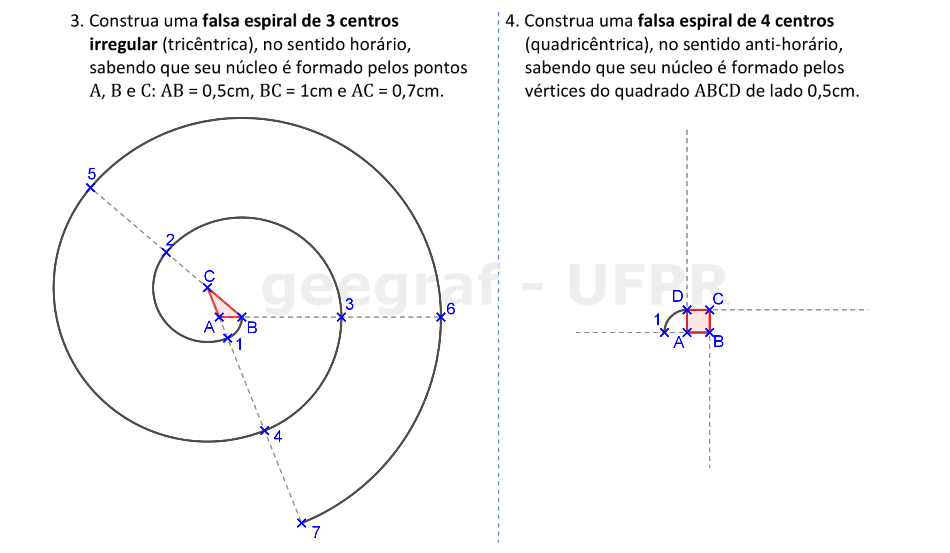
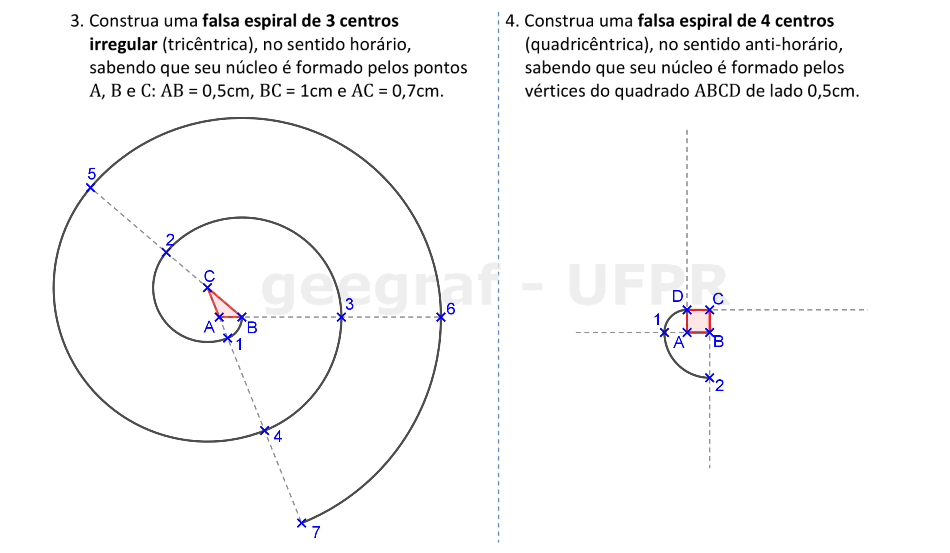
Vamos construir falsas espirais com 3 e com 4 centros.


📏 📐 Solução
Usando o mesmo raciocínio do exercício anterior, podemos construir a espiral ovalada com o núcleo representado pelo retângulo de medidas indicadas.


📏 📐 Resolução
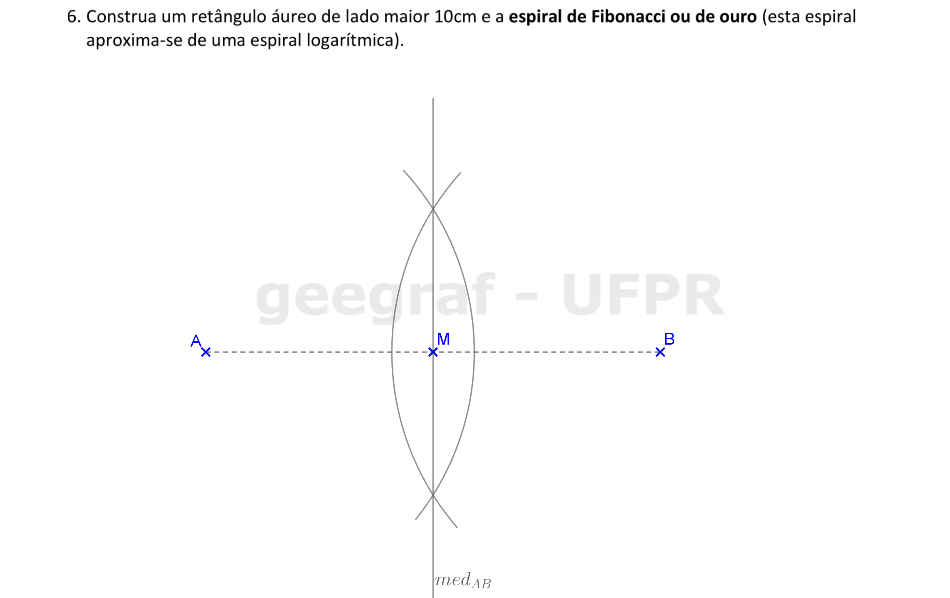
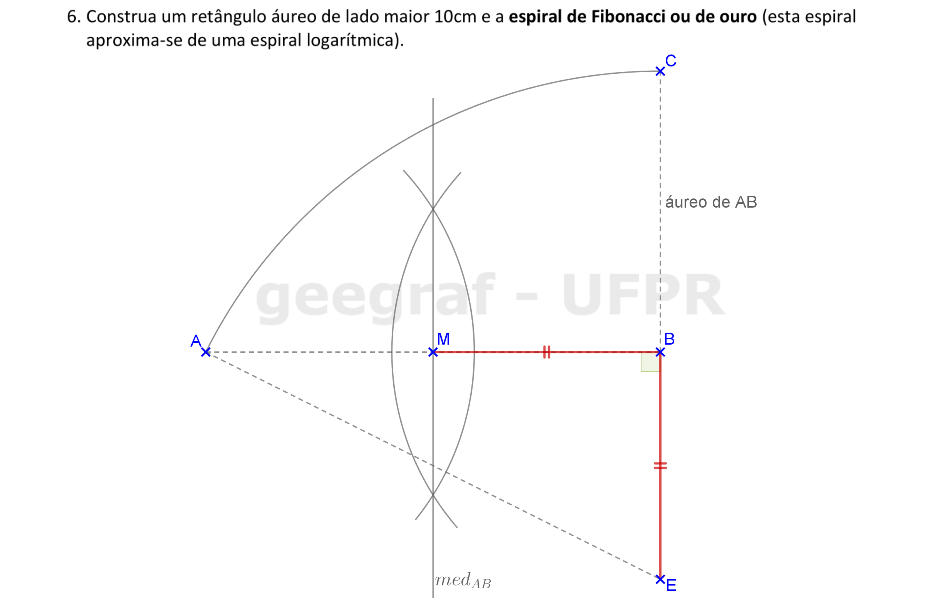
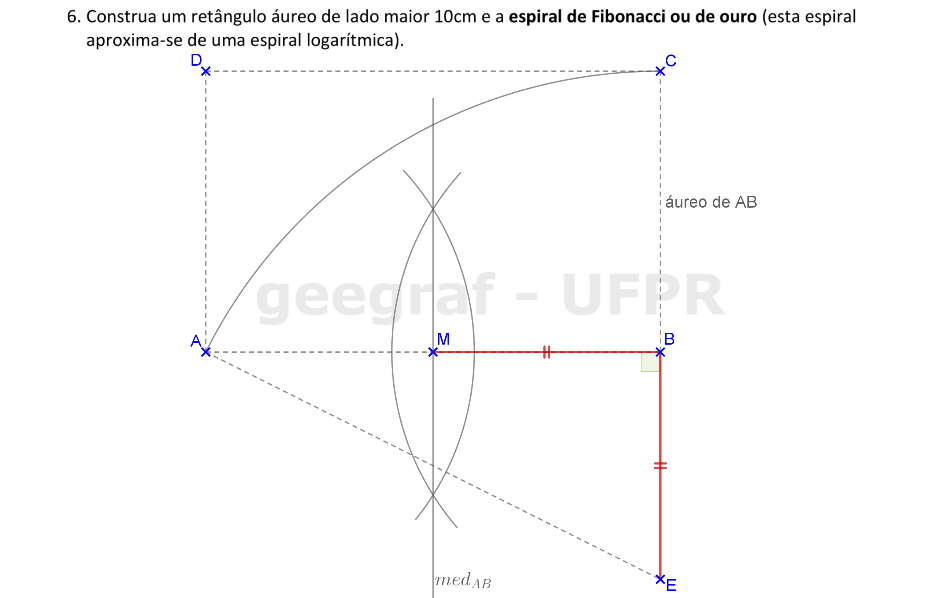
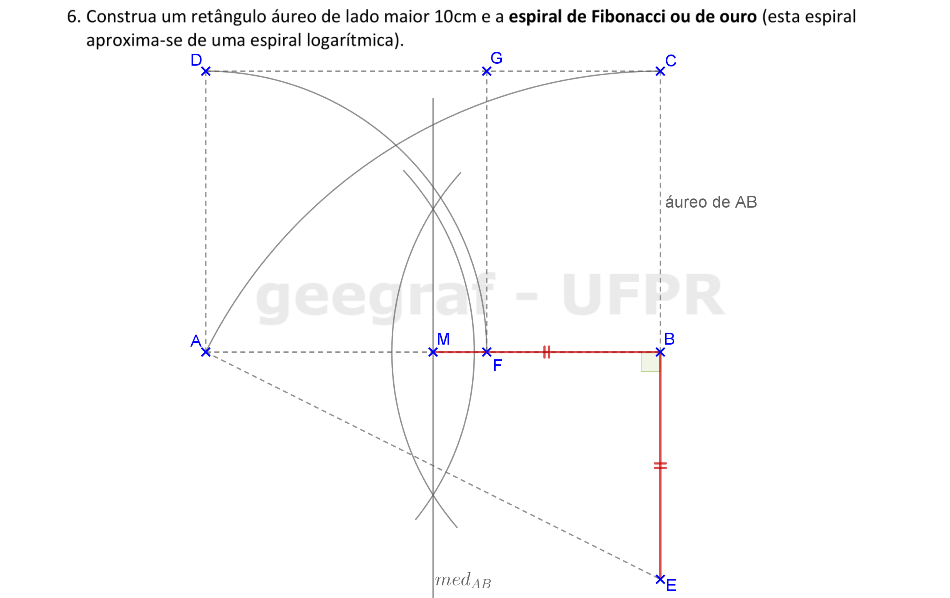
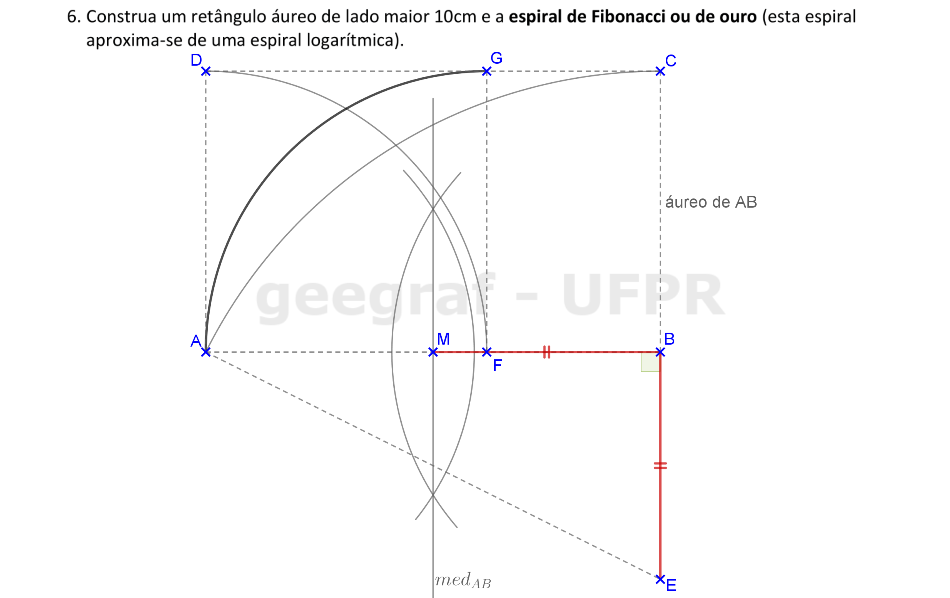
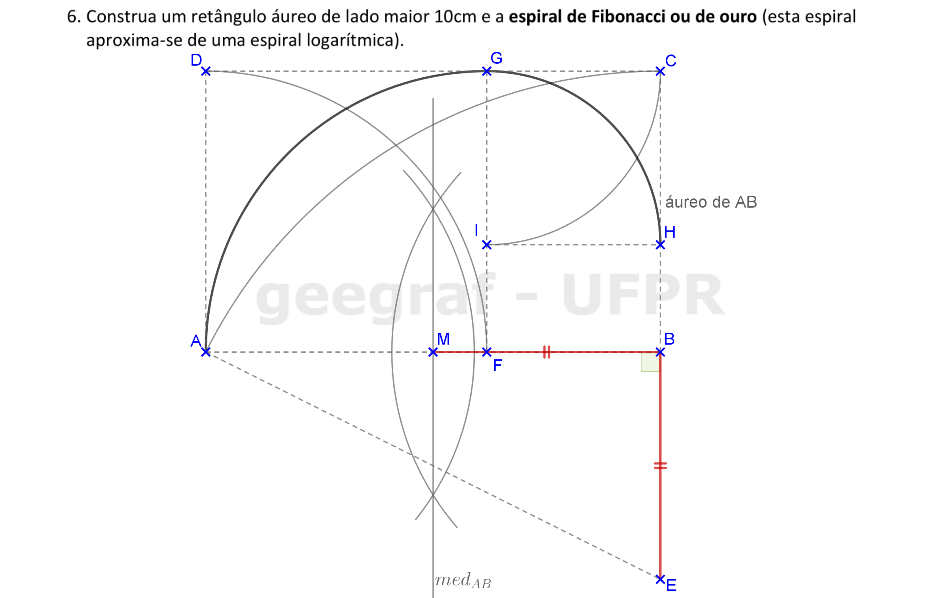
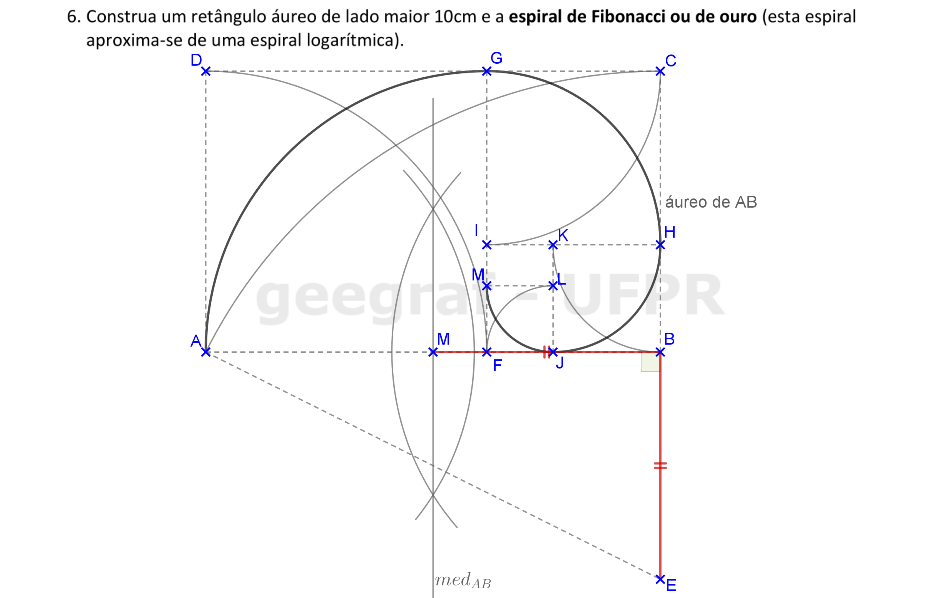
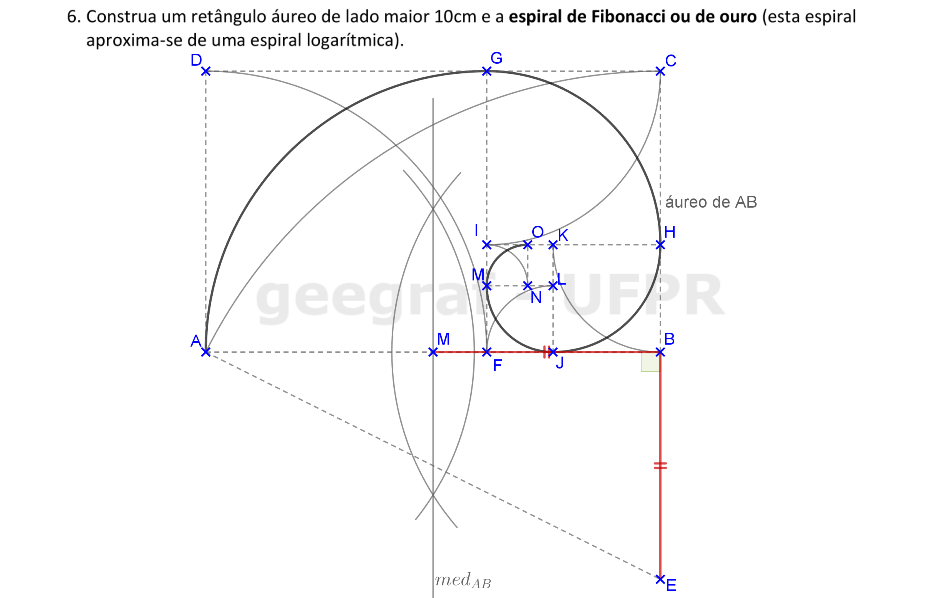
Vamos construir a espiral de ouro começando pela construção do retângulo áureo.


📏 📐 Resolução
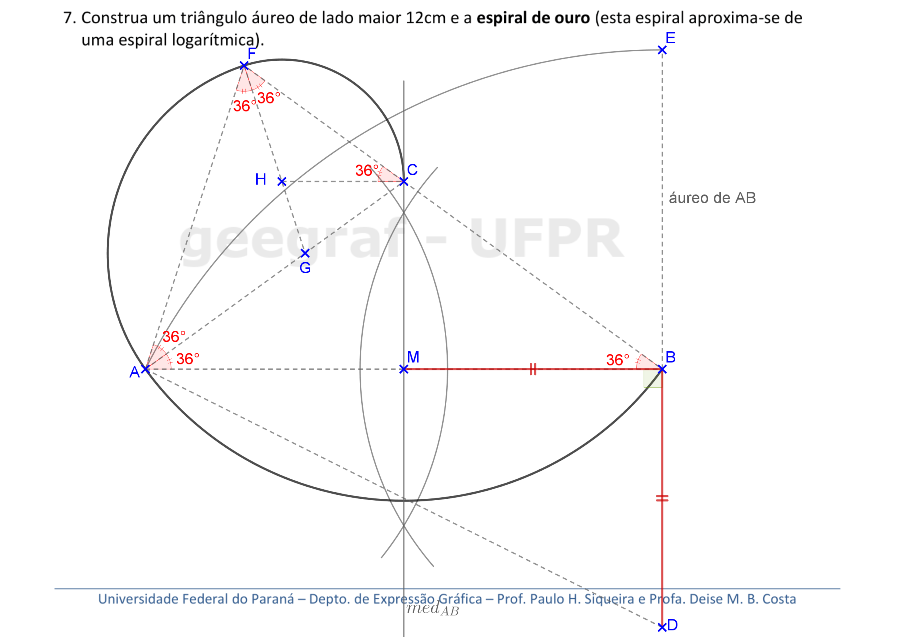
Vamos construir a espiral de ouro começando pela construção do triângulo áureo.


📏 📐 Resolução
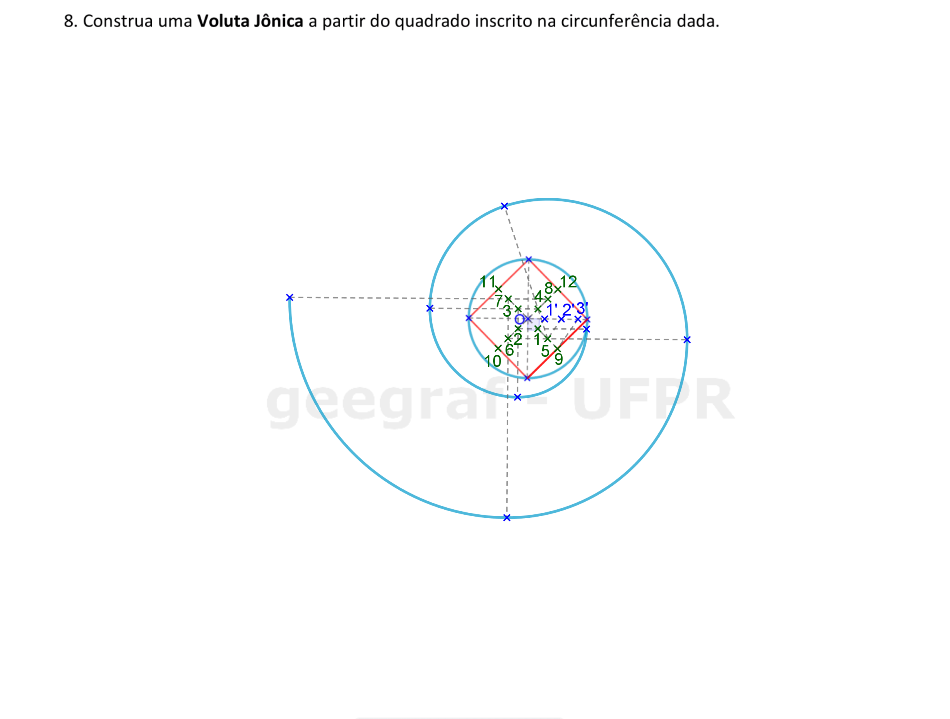
Vamos construir a Voluta Jônica começando pela construção dos segmentos perpendiculares aos lados do quadrado.




📑 Propriedades
Vamos acompanhar a demonstração do teorema de Apollonius para o caso de uma elipse. Considere as esferas inscritas na superfície cônica e tangentes ao plano de seção.



📏 📐 Resolução
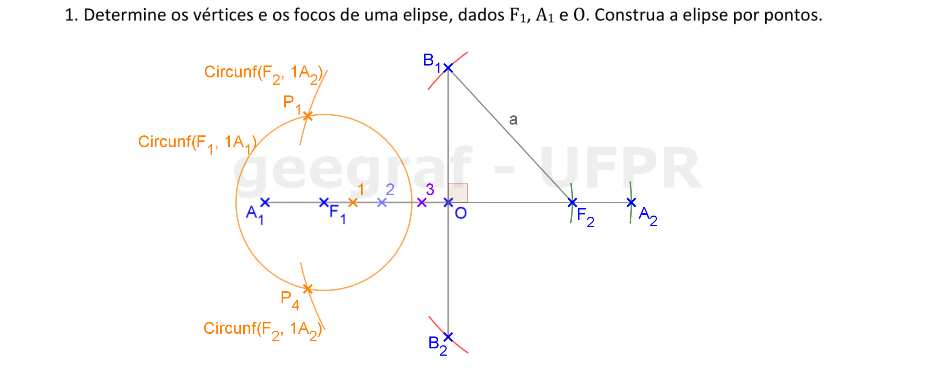
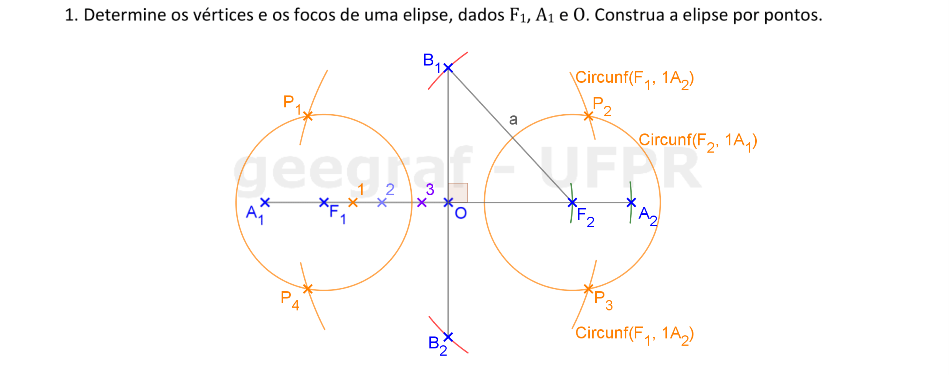
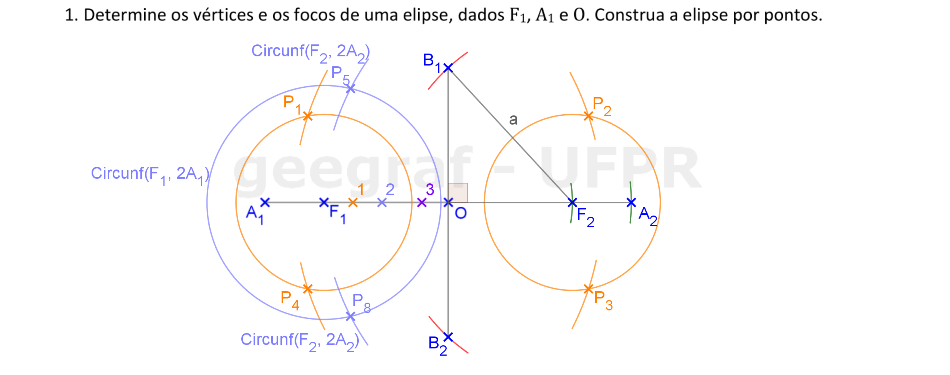
Construiremos uma elipse dados um vértice, o centro e o foco.


📏 📐 Resolução
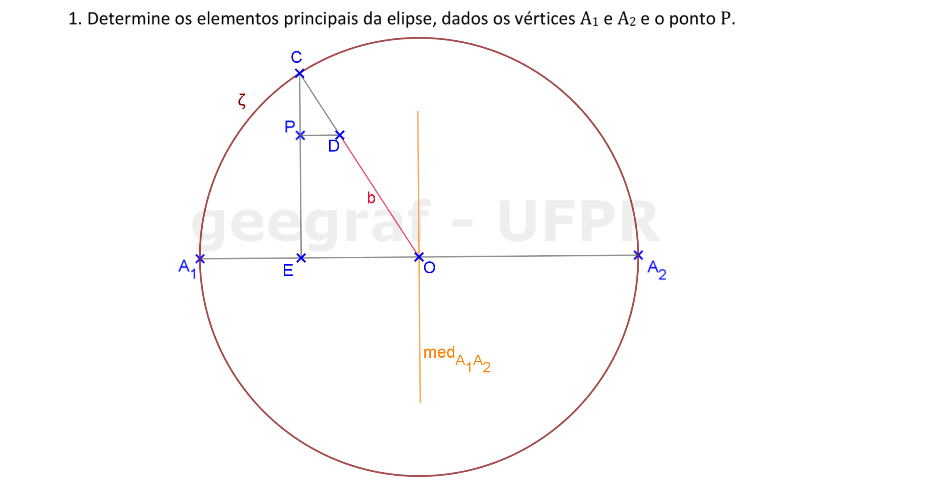
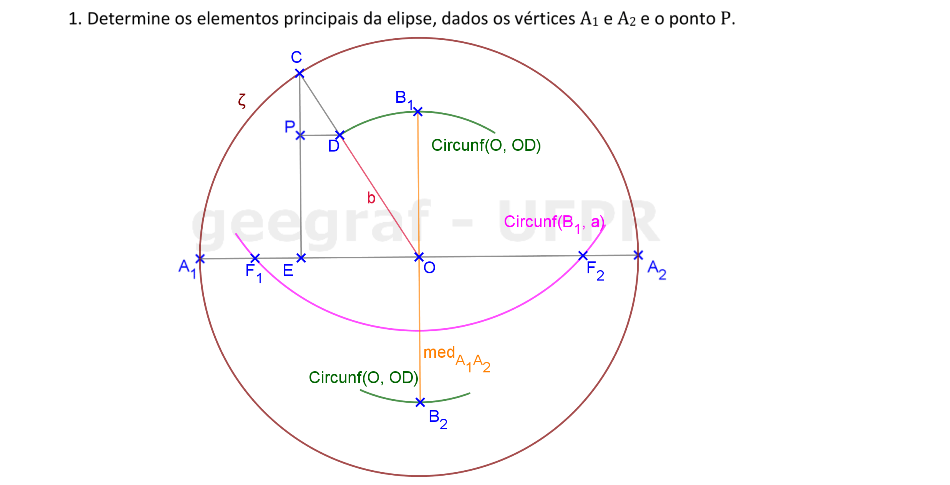
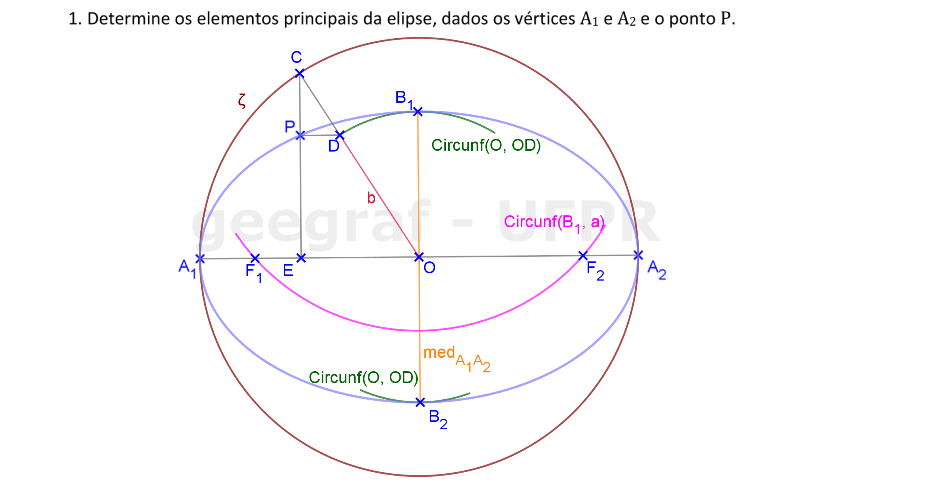
Vamos construir os elementos principais de uma elipse dados os focos e um ponto da cônica.


📏 📐 Resolução
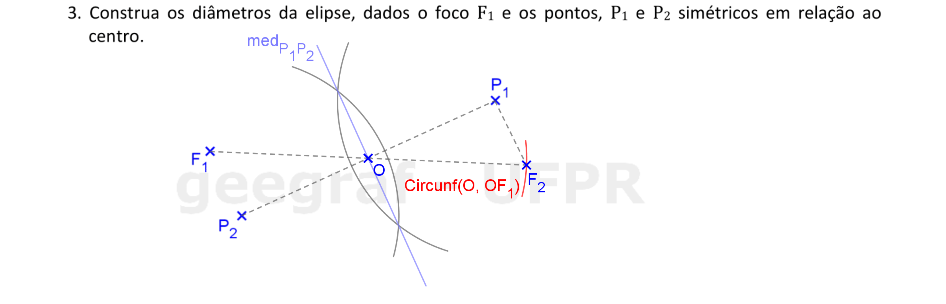
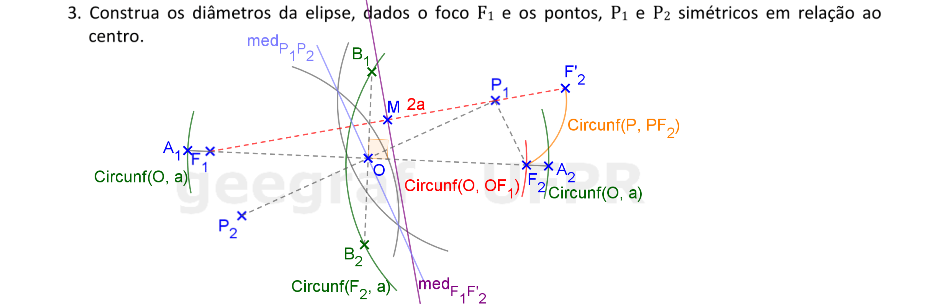
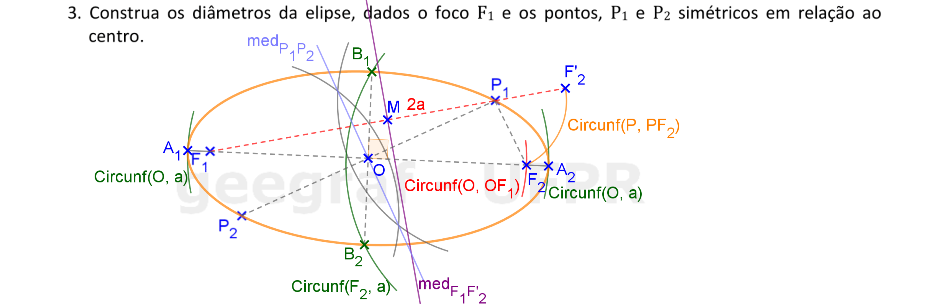
Vamos construir os elementos principais de uma elipse dados os pontos simétricos em relação ao centro e um foco da cônica.

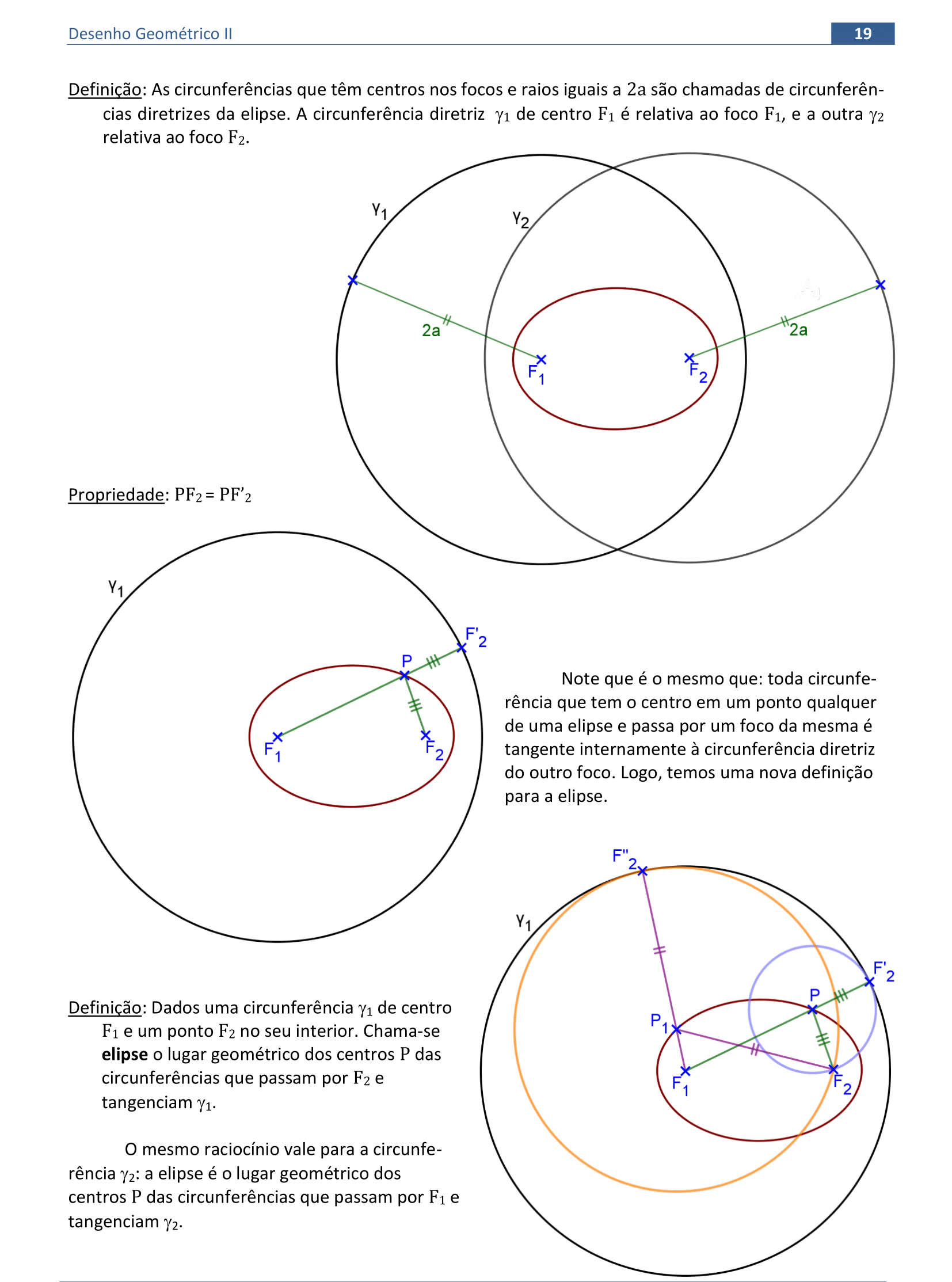

📏 📐 Resolução
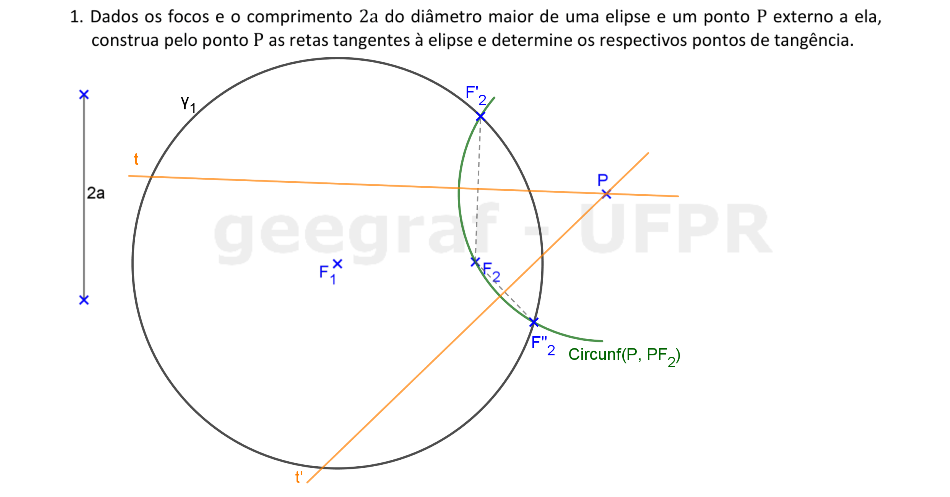
Vamos construir as retas tangentes a uma elipse dada pelos focos, a distância 2a e um ponto da cônica.


📏 📐 Resolução
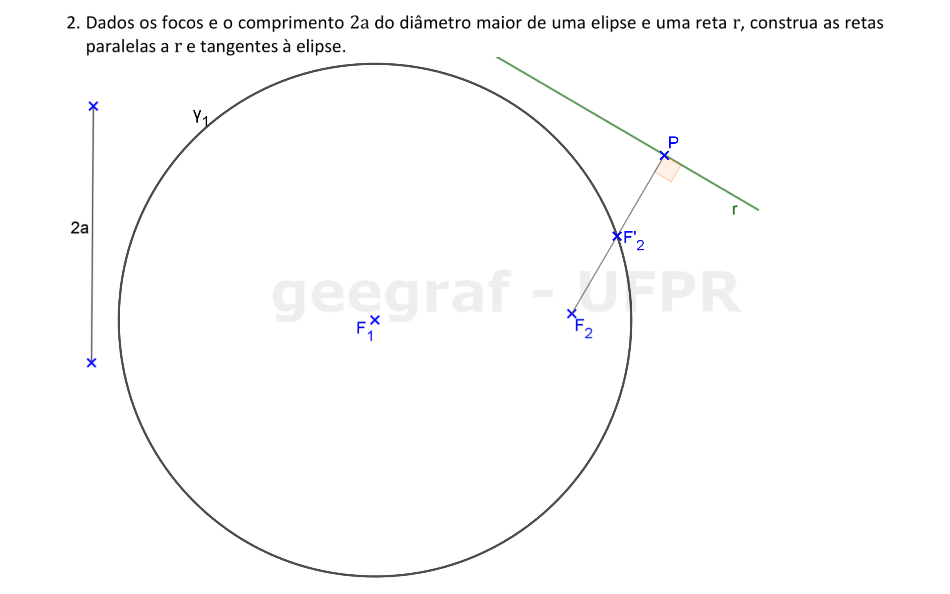
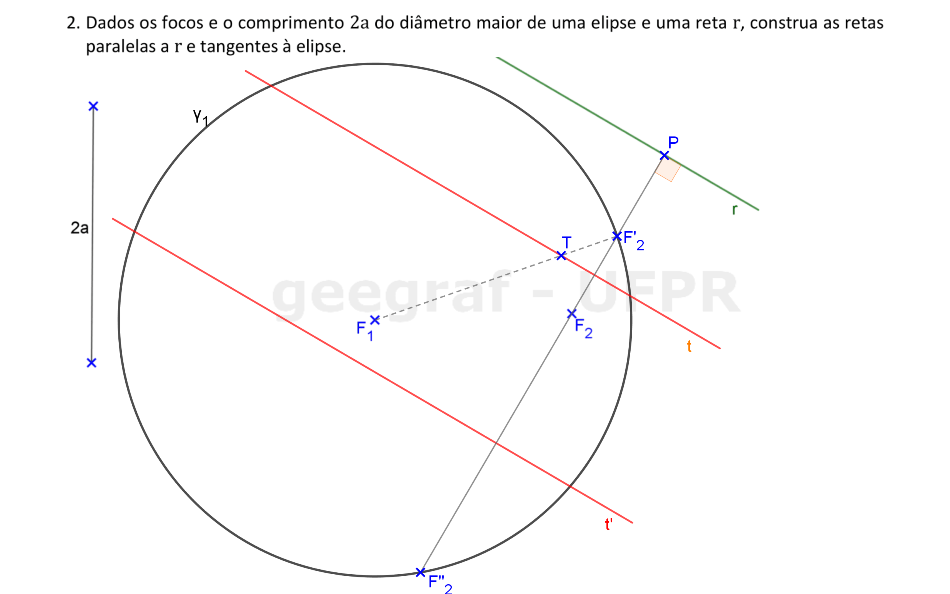
Vamos construir as retas tangentes a uma elipse paralelas a uma reta. São dados os focos e a distância 2a da cônica.



📏 📐 Resolução
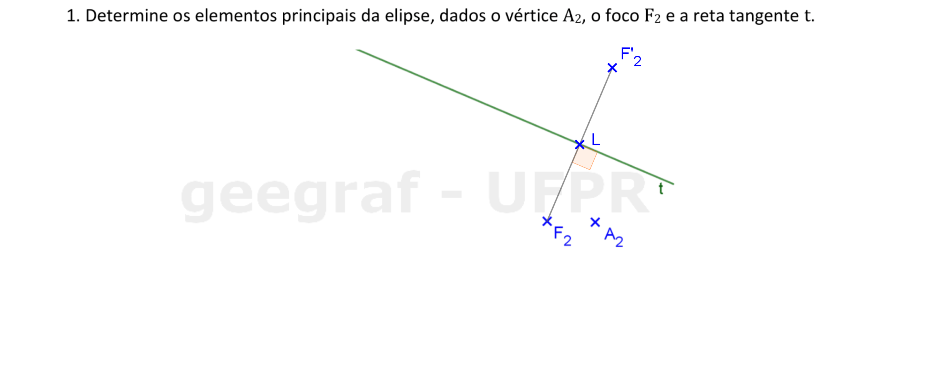
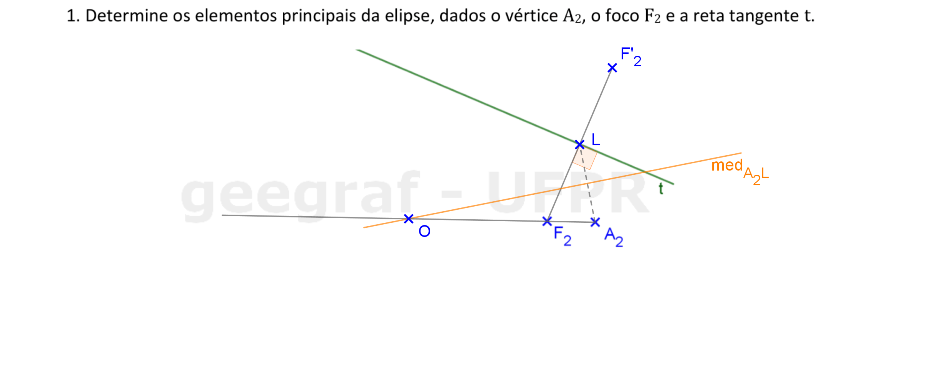
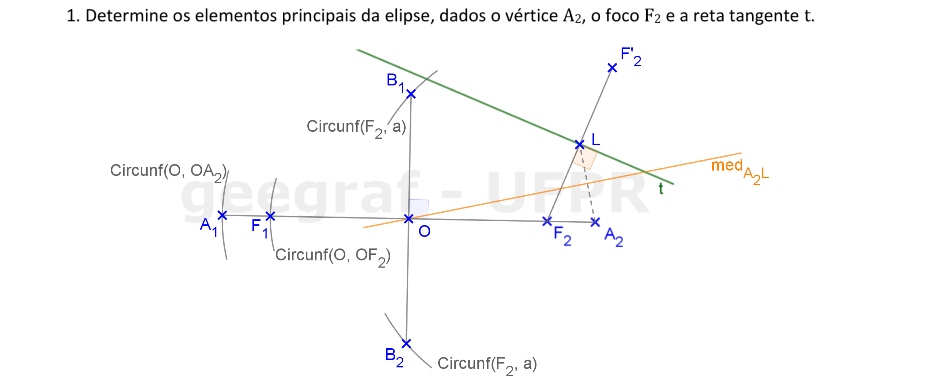
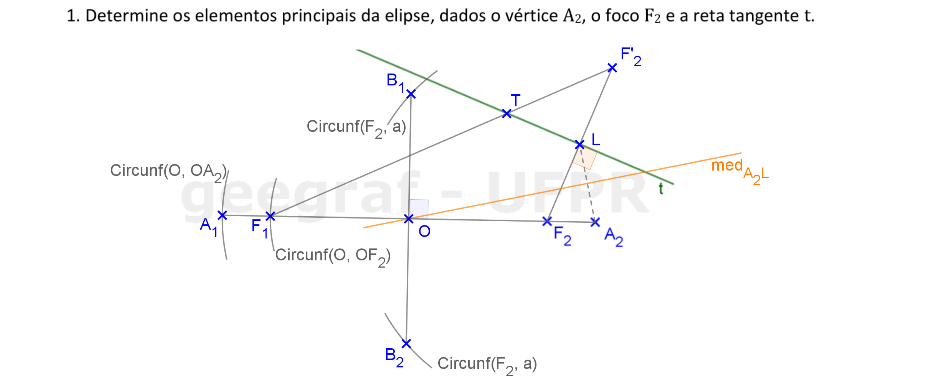
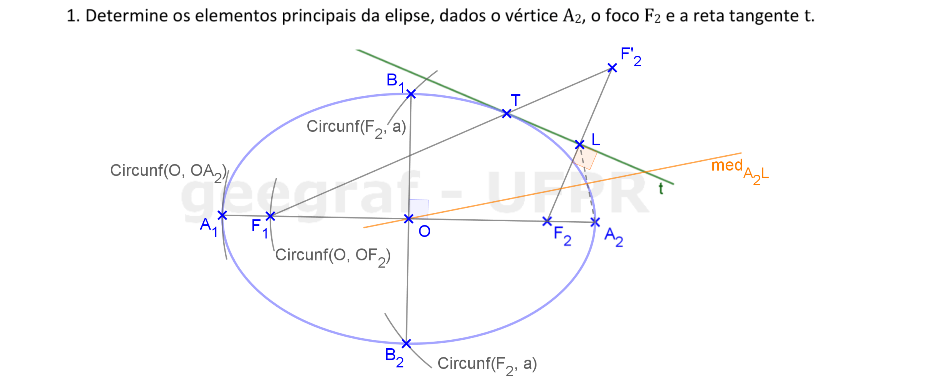
Vamos construir os elementos principais de uma elipse dada por um vértice, um foco e uma reta tangente.


📏 📐 Resolução
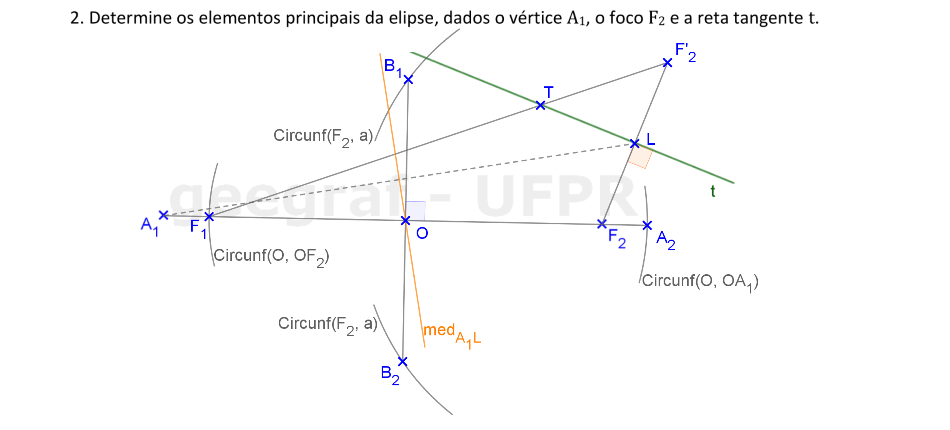
Vamos construir os elementos principais de uma elipse dada por um vértice, um foco e uma reta tangente.



📏 📐 Resolução
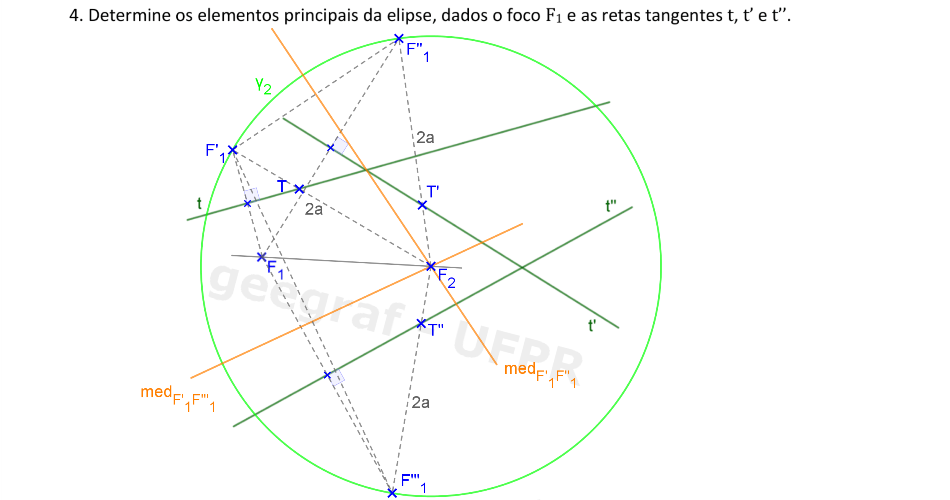
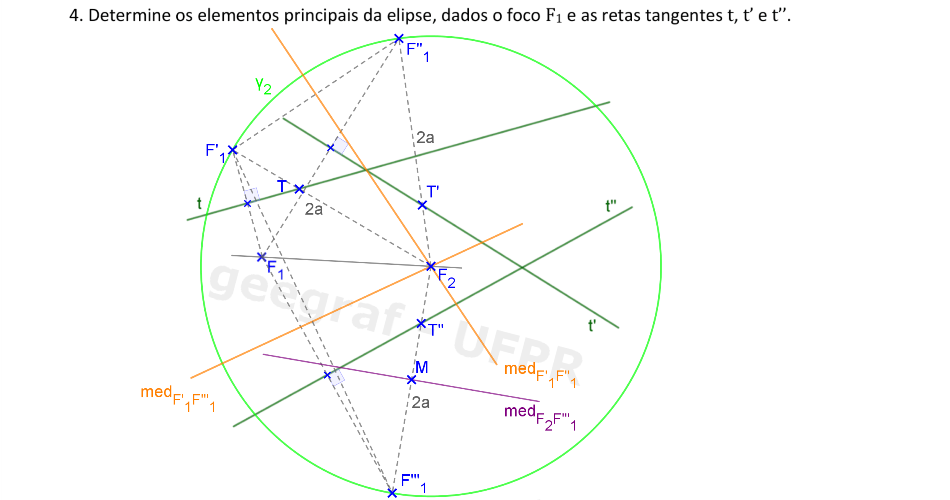
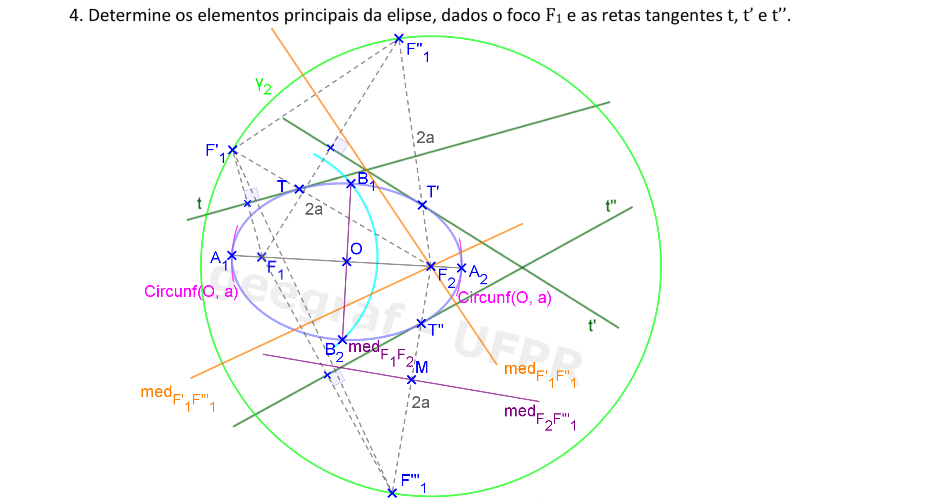
Vamos construir os elementos principais de uma elipse dada por um foco e 3 retas tangentes.




📏 📐 Resolução
Vamos construir os elementos principais de uma elipse dada pelos vértices do diâmetro principal e um ponto.


📏 📐 Resolução
Vamos construir os elementos principais de uma elipse dada pelo diâmetro 2c e pela excentricidade.



📏 📐 Resolução
Vamos construir os elementos principais de uma elipse dada pelo diâmetro 2a e pela excentricidade.

3. Hipérboles e parábolas
Material da página 26 até a página 43.

📑 Propriedades
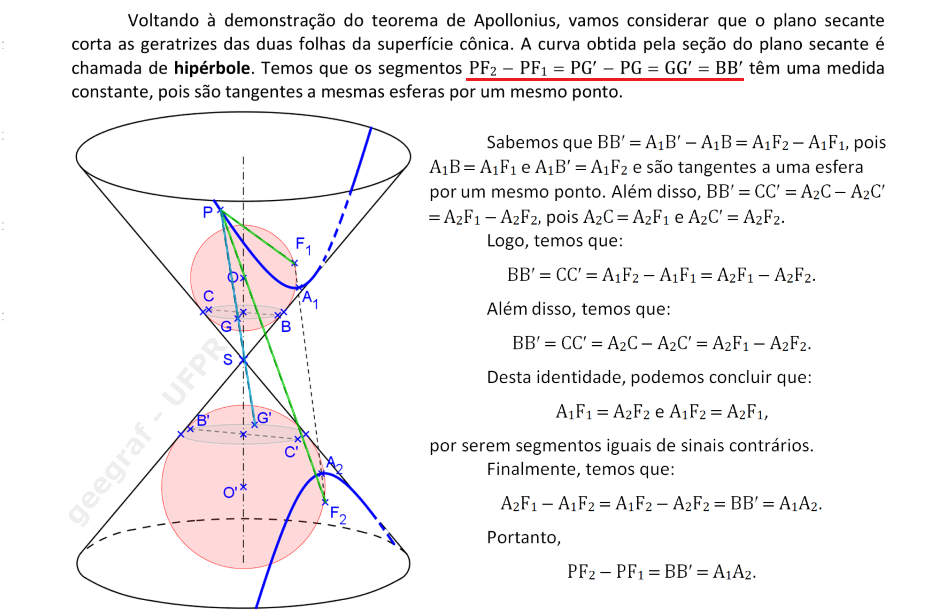
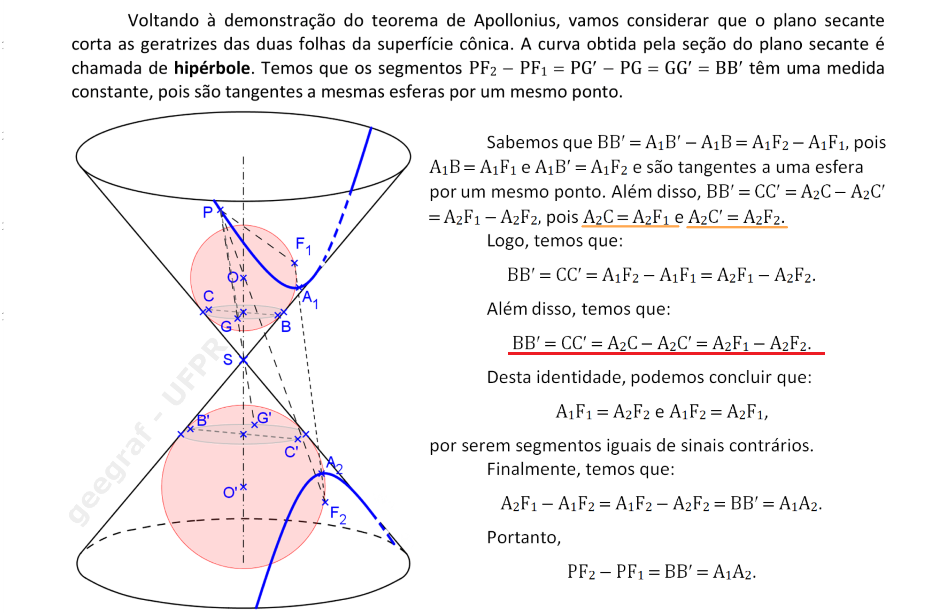
Vamos acompanhar a demonstração do teorema de Apollonius para o caso de uma hipérbole. Considere as esferas inscritas na superfície cônica e tangentes ao plano de seção.
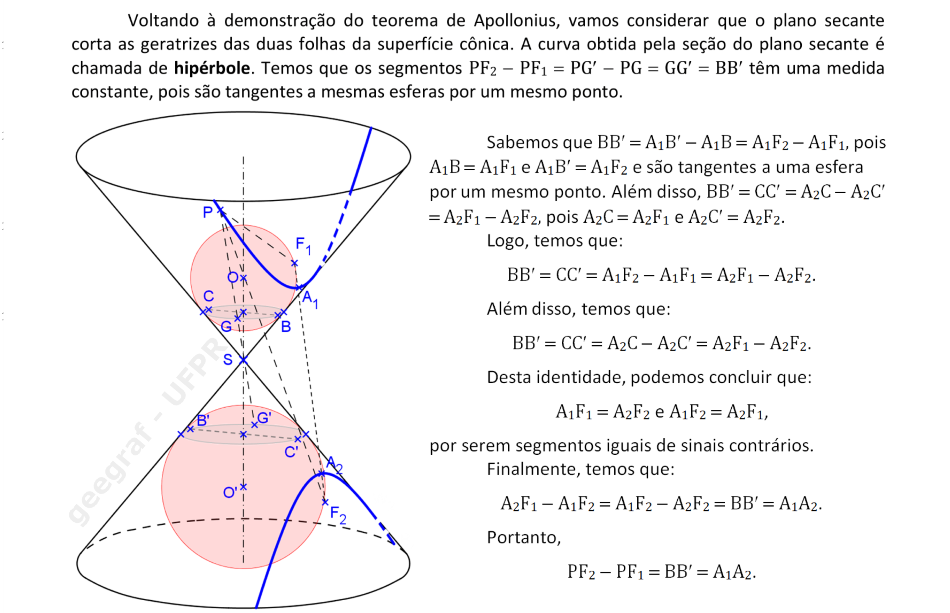


📏 📐 Resolução
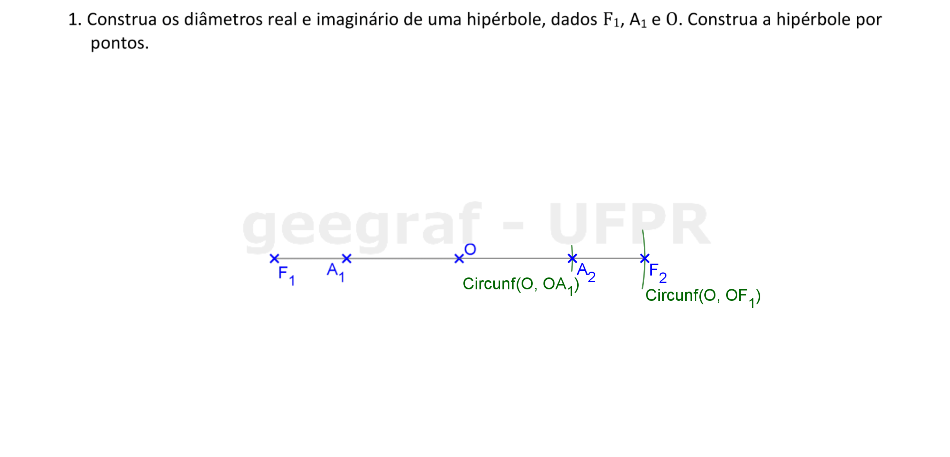
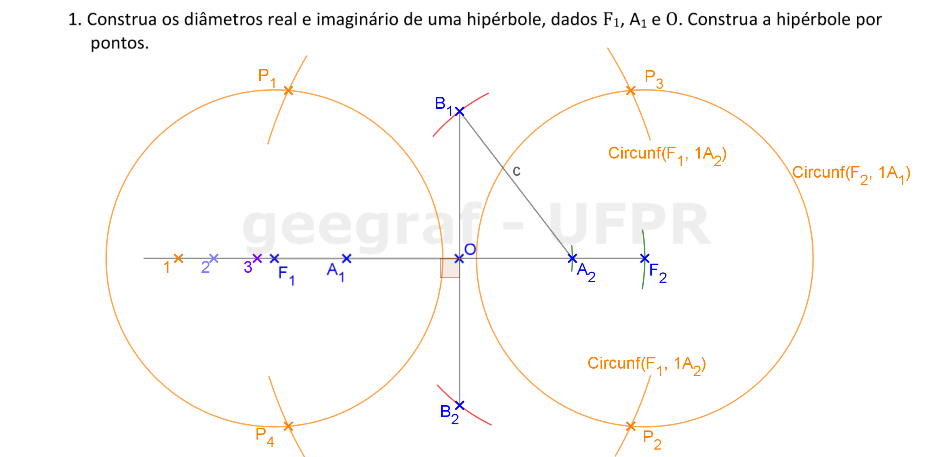
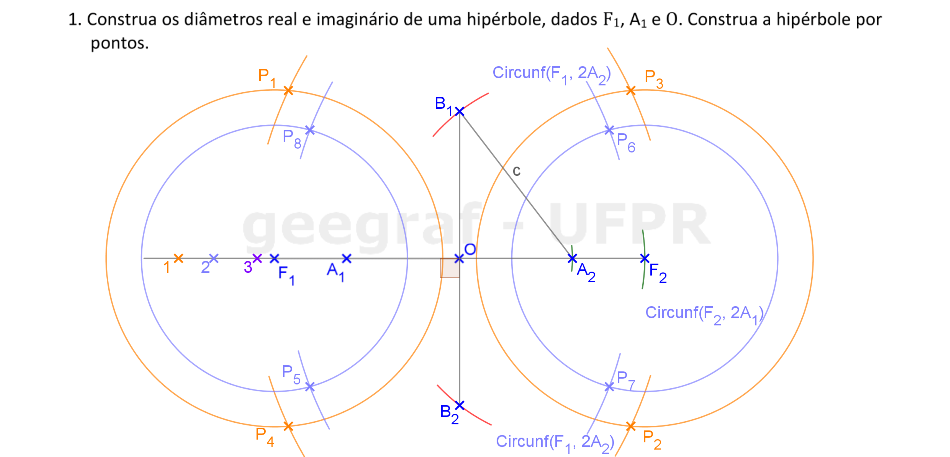
Construiremos uma hipérbole dados um vértice, o centro e um foco.


📏 📐 Resolução
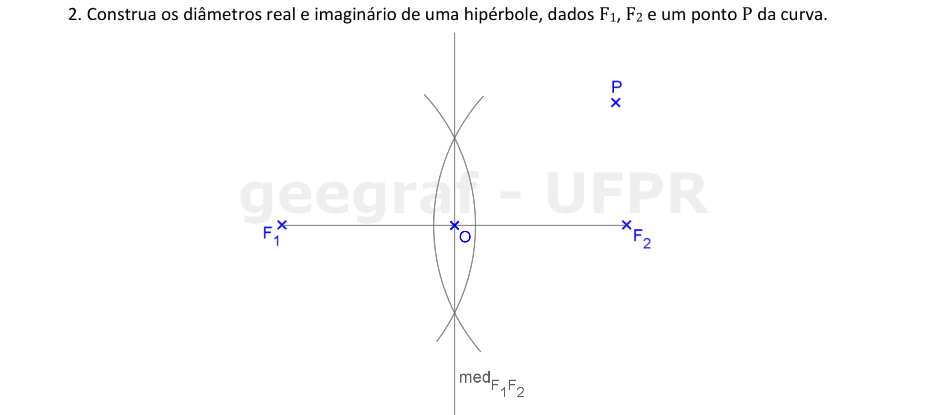
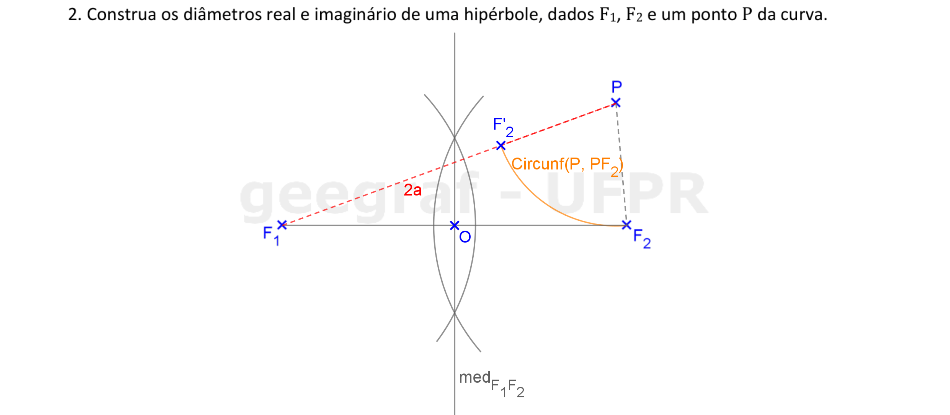
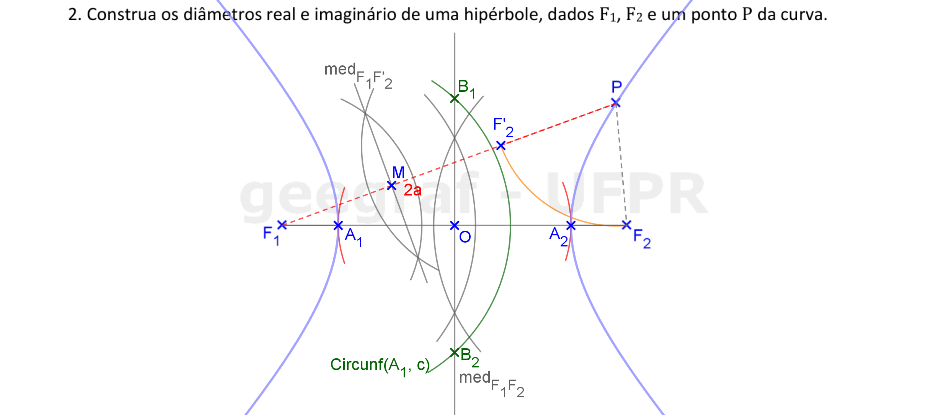
Vamos encontrar os elementos principais de uma hipérbole dados os focos, e um ponto da curva.



📏 📐 Resolução
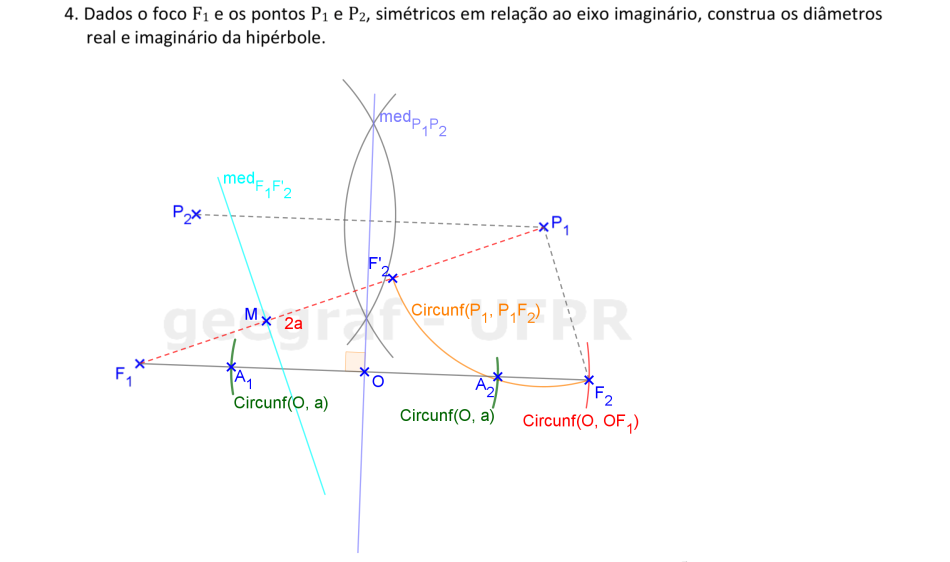
Encontraremos os elementos principais de uma hipérbole um foco e os pontos simétricos em relação ao eixo imaginário.


📏 📐 Resolução
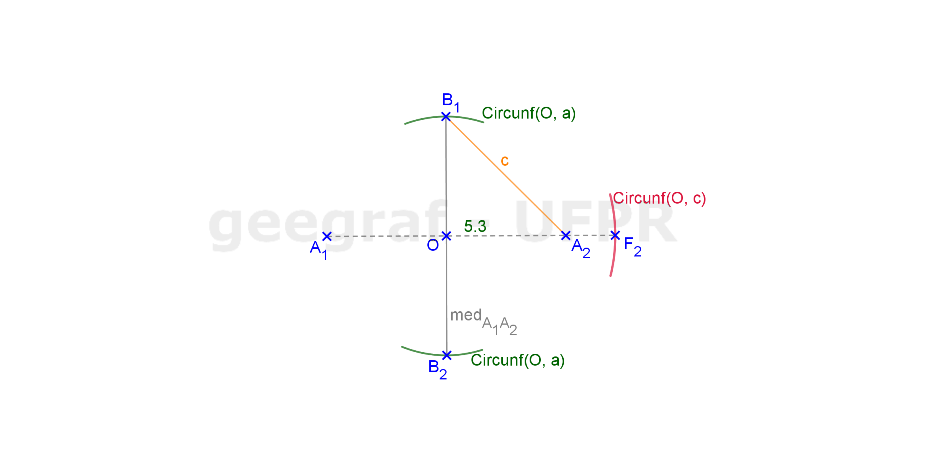
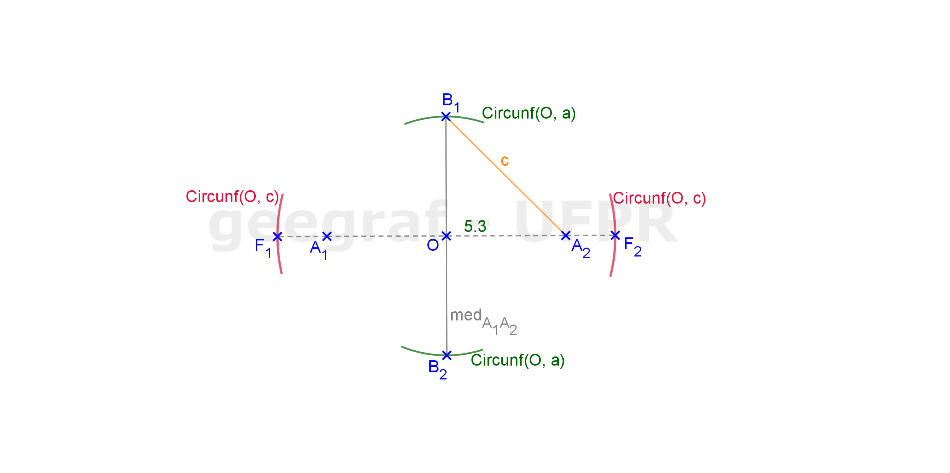
Vamos construir os elementos principais de uma hipérbole dada pelo diâmetro 2a e pela excentricidade.


📏 📐 Resolução
Vamos construir os elementos principais de uma hipérbole dada pelo diâmetro 2c e pela excentricidade.





📏 📐 Resolução
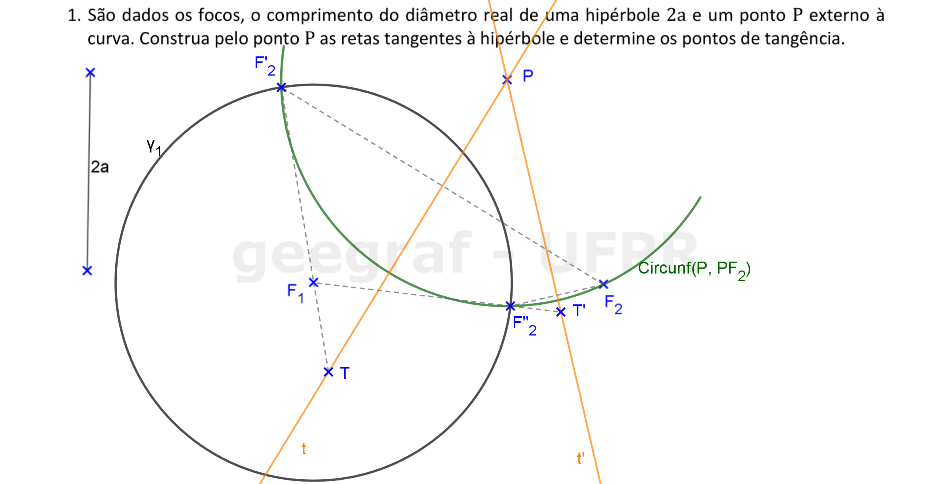
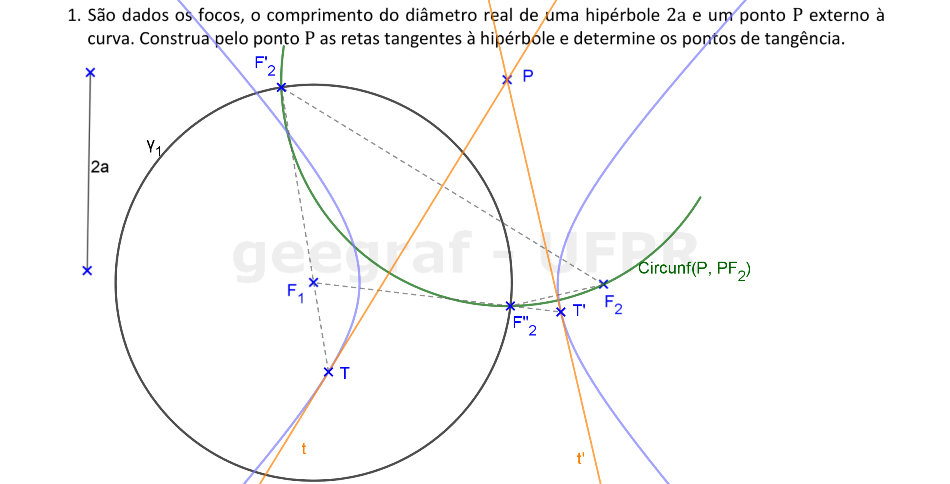
Vamos construir as retas tangentes à hipérbole, dada pelos focos e pela distância 2a, que passam pelo ponto P.


📏 📐 Resolução
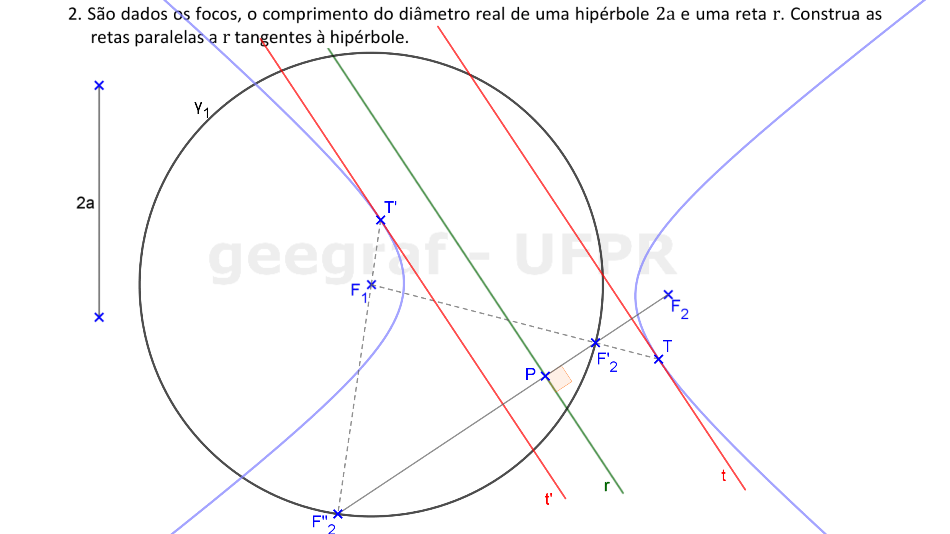
Vamos construir as retas tangentes à hipérbole, dada pelos focos e pela distância 2a, que são paralelas à reta r.




📏 📐 Resolução
Vamos construir as assíntotas da hipérbole, dada pelos focos e pelo diâmetro principal 2a.

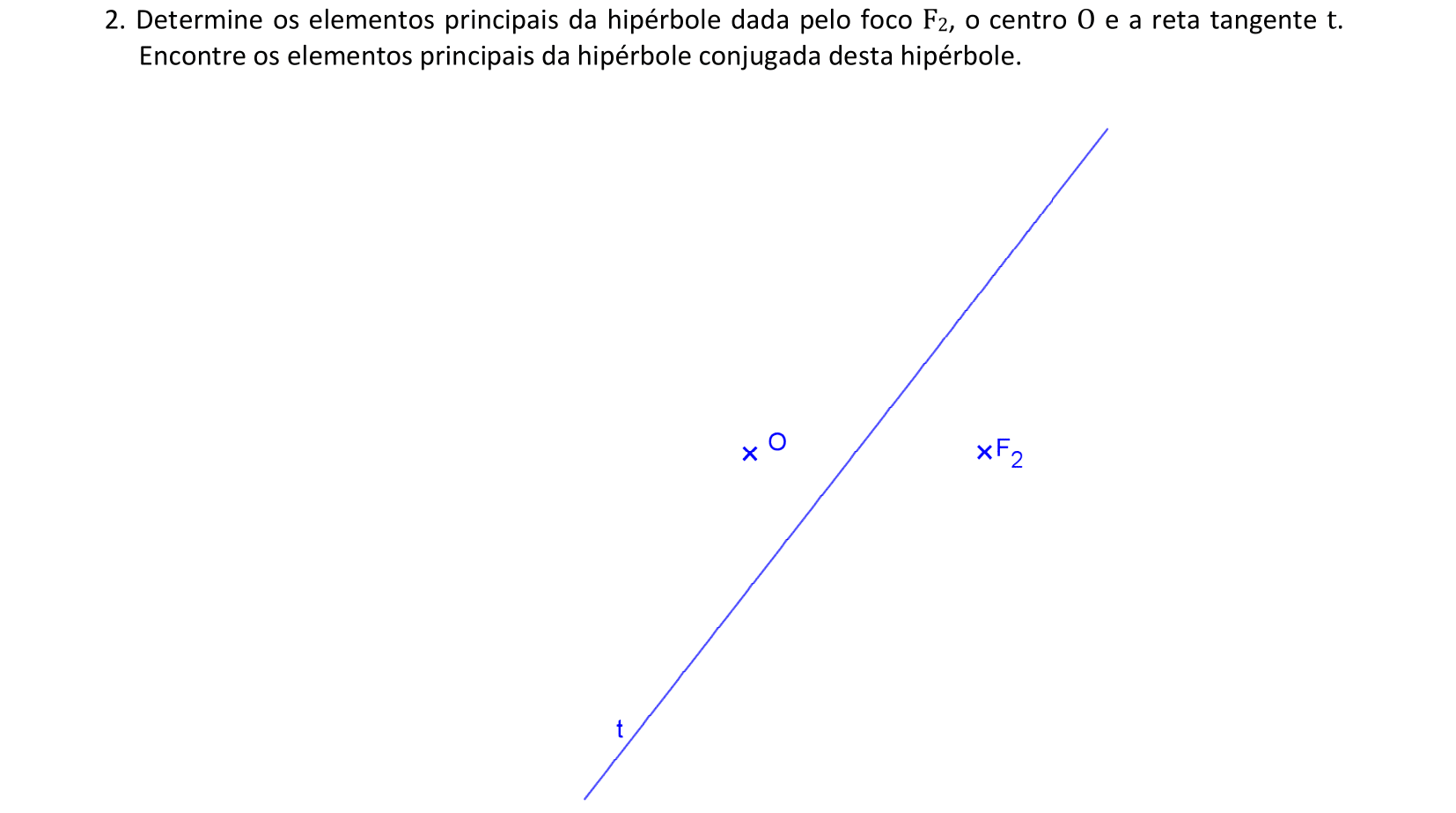
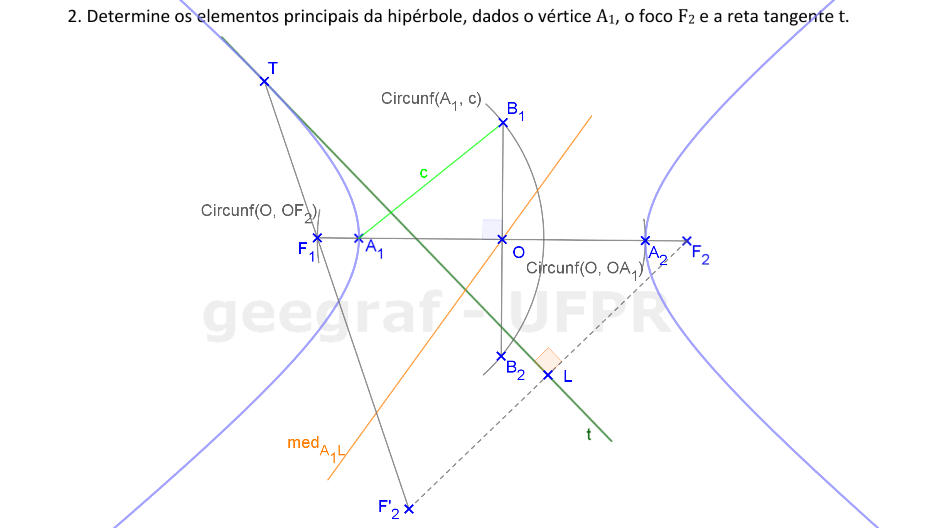
📏 📐 Resolução
Vamos encontrar os elementos principais da hipérbole, dada por um foco, o centro e uma reta tangente. Além disso, vamos encontrar os elementos principais da hipérbole conjugada desta cônica.


📏 📐 Resolução
Vamos construir os elementos principais de uma hipérbole equilátera, dada pelo diâmetro principal 2a.




📏 📐 Resolução
Vamos construir os elementos principais de uma hipérbole dada por um foco, um vértice e uma reta tangente.


📏 📐 Resolução
Vamos construir os elementos principais de uma hipérbole dada por um foco, um vértice e uma reta tangente.


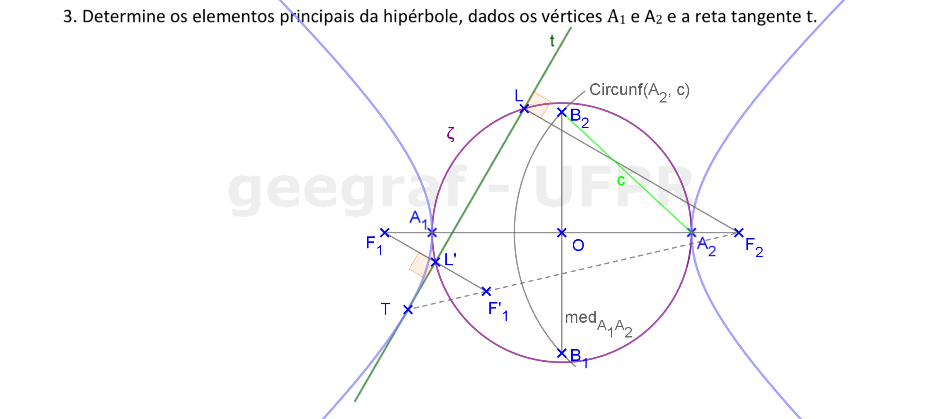
📏 📐 Resolução
Vamos construir os elementos principais de uma hipérbole dada pelo diâmetro real e uma reta tangente.


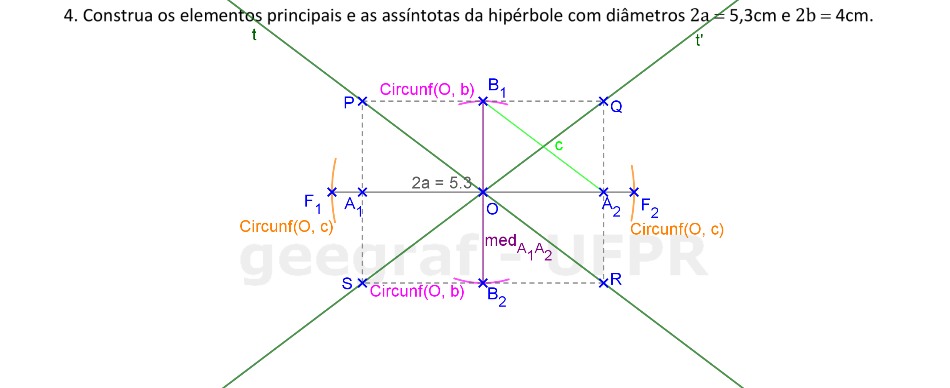
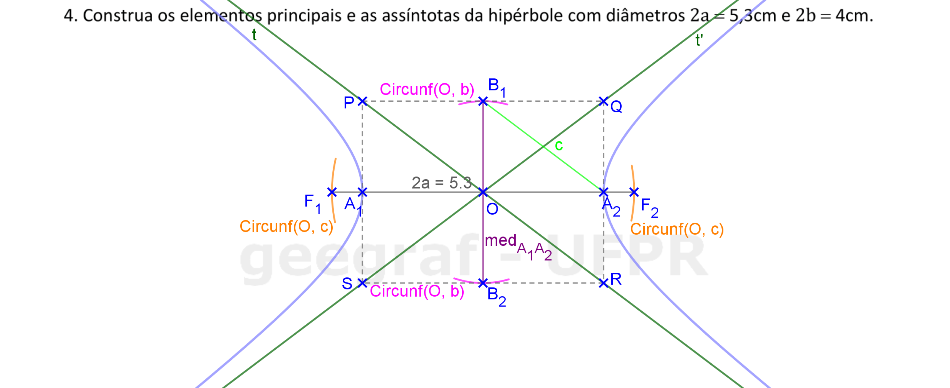
📏 📐 Resolução
Vamos construir os elementos principais e as assíntotas de uma hipérbole dada pelos diâmetros real e imaginário.



📑 Propriedades
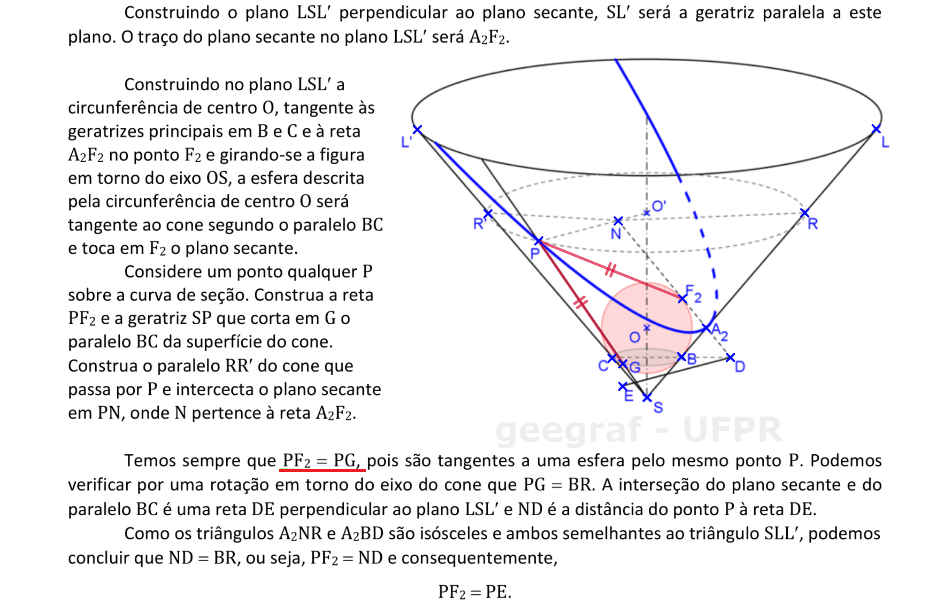
Vamos acompanhar a demonstração do teorema de Apollonius para o caso de uma parábola. Considere a esfera inscrita na superfície cônica e tangente ao plano de seção.



📏 📐 Resolução
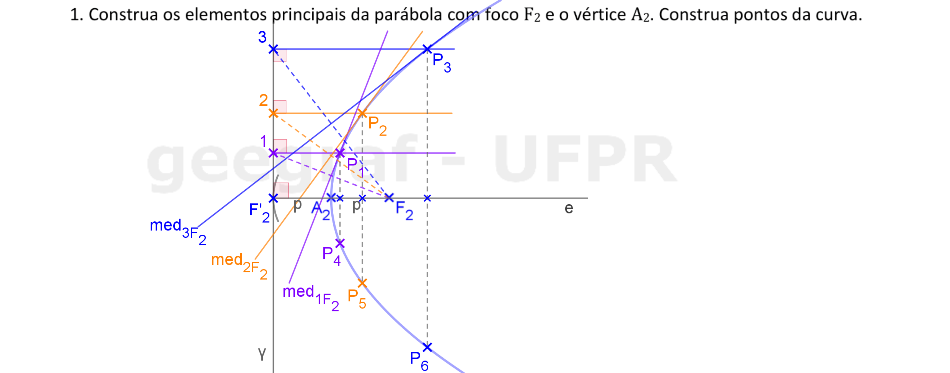
Vamos construir os elementos principais e alguns pontos de uma parábola dada pelo vértice e pelo foco.


📏 📐 Resolução
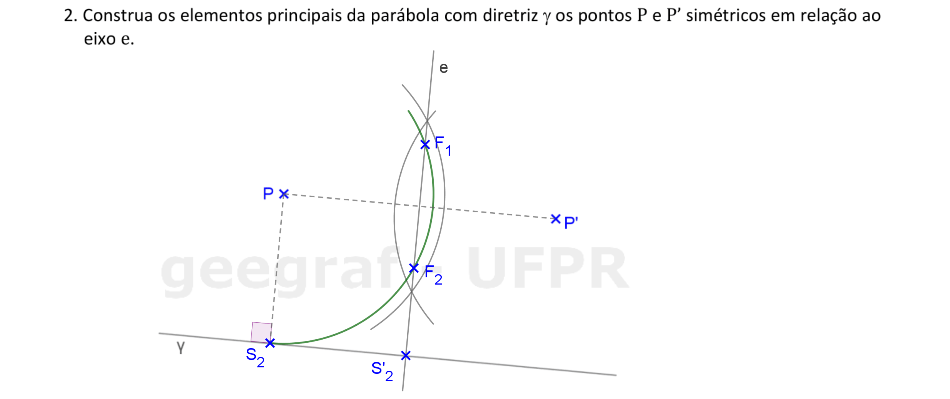
Vamos construir os elementos principais de uma parábola dada pelos pontos simétricos em relação ao eixo e a reta diretriz.


📏 📐 Resolução
Vamos construir os elementos principais de uma parábola dada pela direção da diretriz, o foco e um ponto da curva.



📏 📐 Resolução
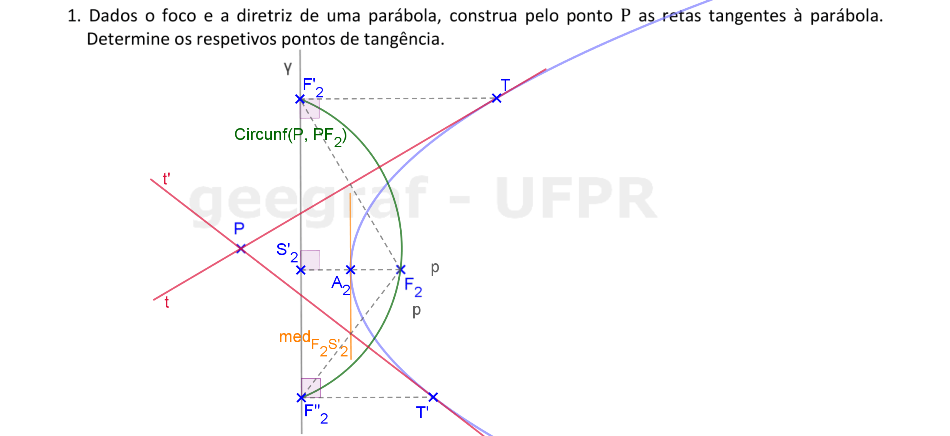
Vamos construir as retas tangentes à parábola que passam por um ponto. São dados o foco e a diretriz da cônica.


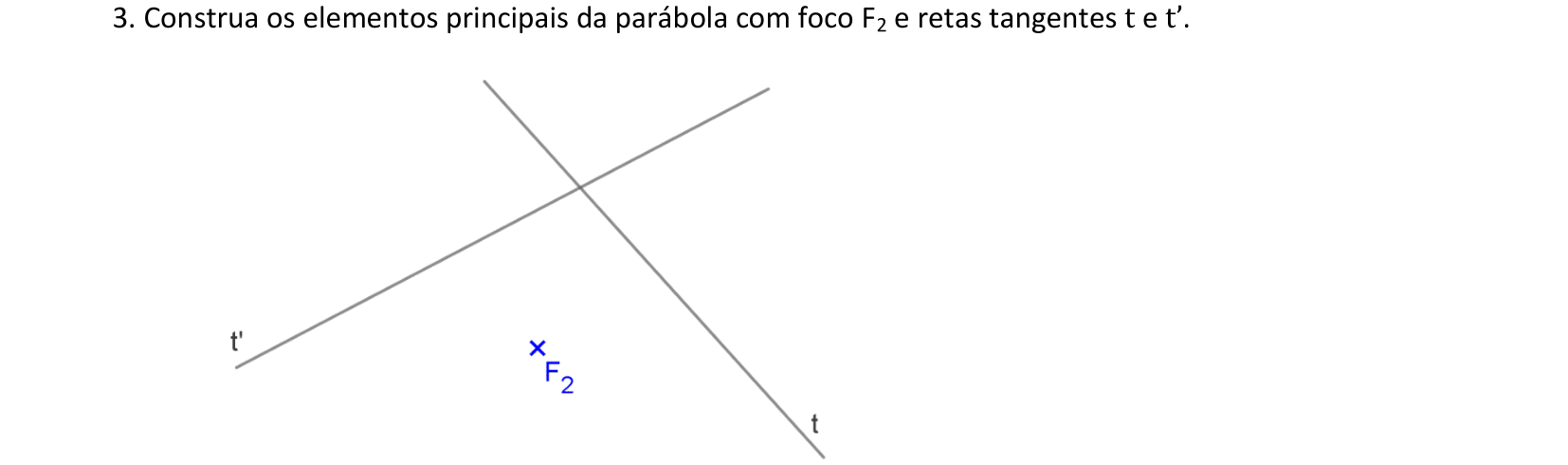
📏 📐 Resolução
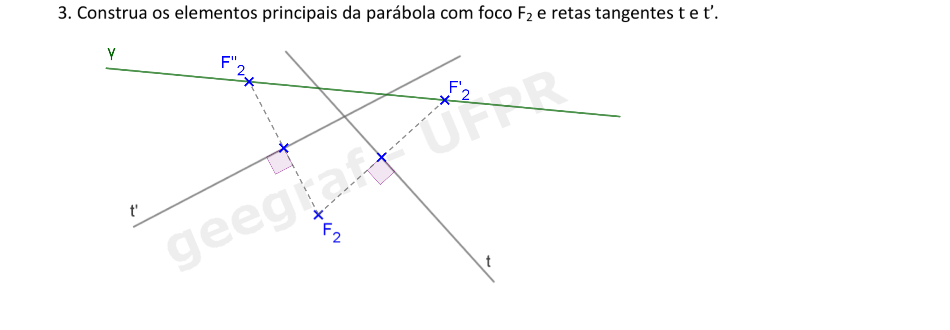
Vamos construir os elementos principais de uma parábola dada por duas retas tangentes e o foco.

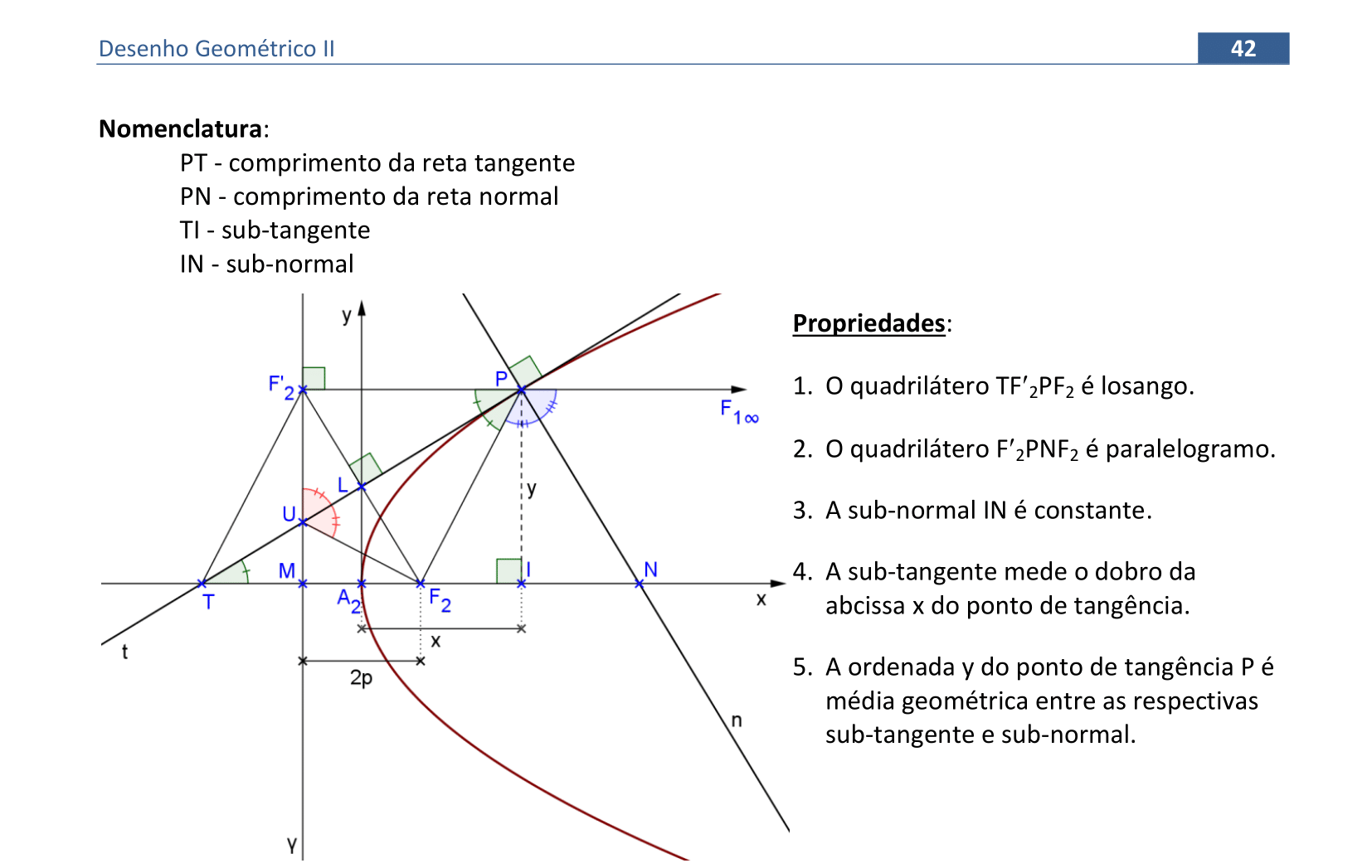
📑 Propriedades
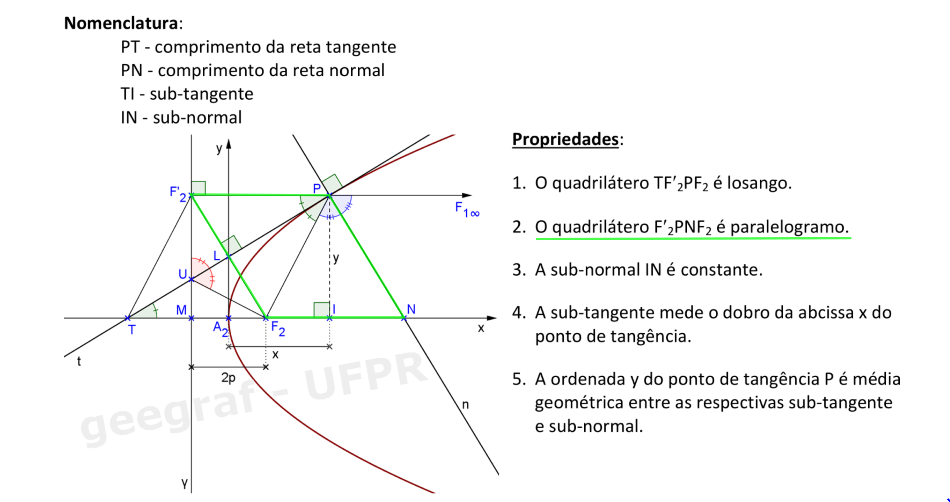
Vamos compreender as propriedades sobre retas tangentes e normais de uma parábola.


📏 📐 Resolução
Vamos construir os elementos principais de uma parábola dada pelo eixo, uma reta tangente e um ponto da parábola pertencente à reta tangente.


📏 📐 Resolução
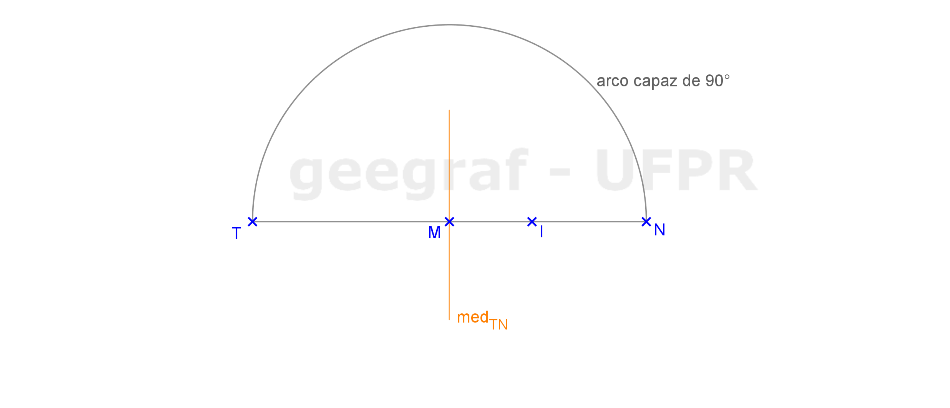
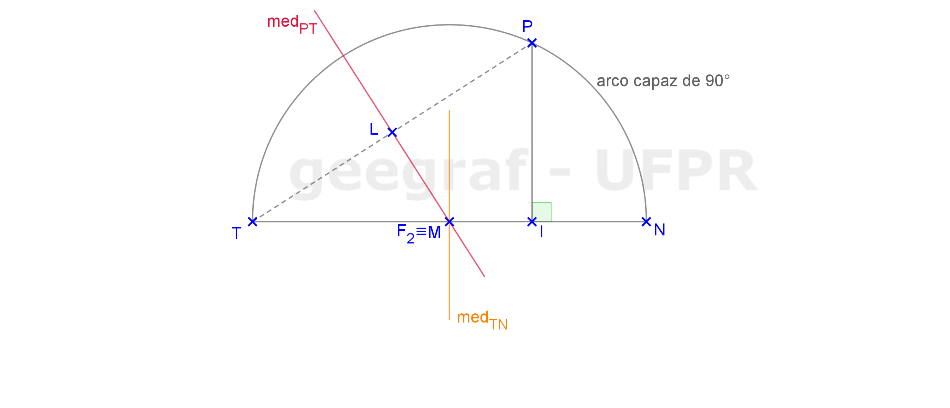
Vamos construir os elementos principais de uma parábola dada pelos segmentos sub-tangente e sub-normal.

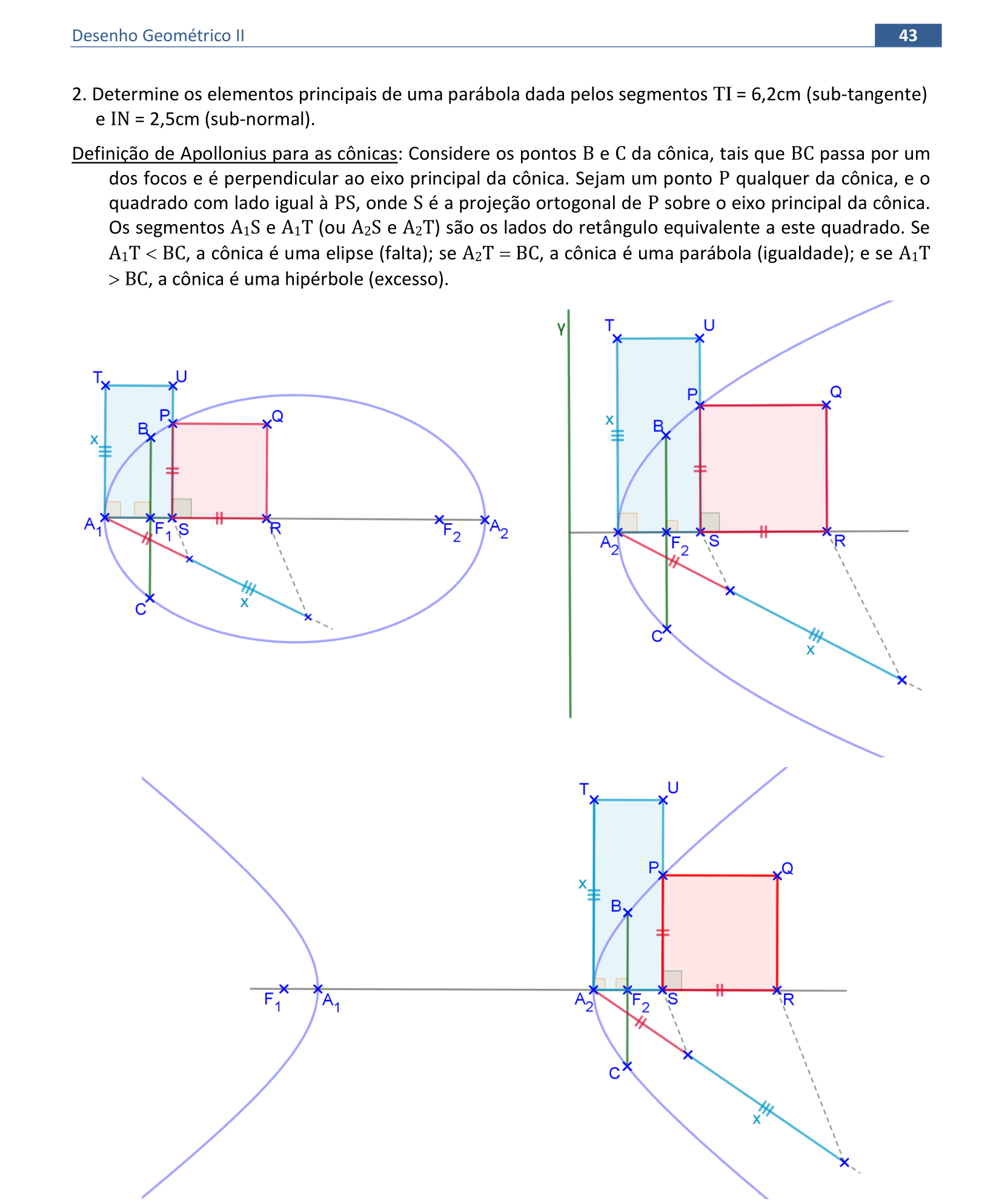
📑 Propriedades
Vamos acompanhar as propriedades que aparecem na definição de Apollonius para as cônicas.
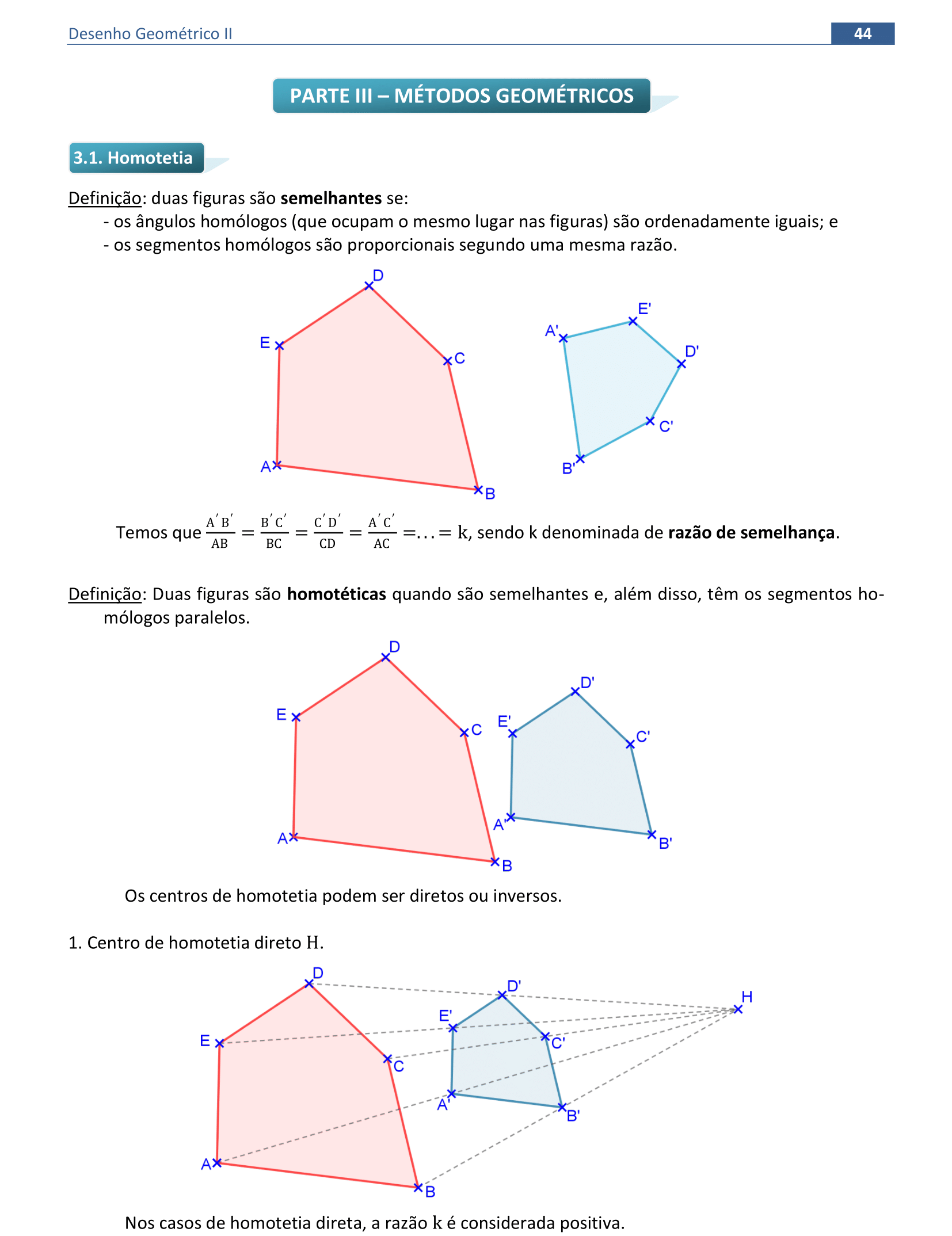
4. Homotetia, Rotação e curvas
Material da página 44 até a página 54.

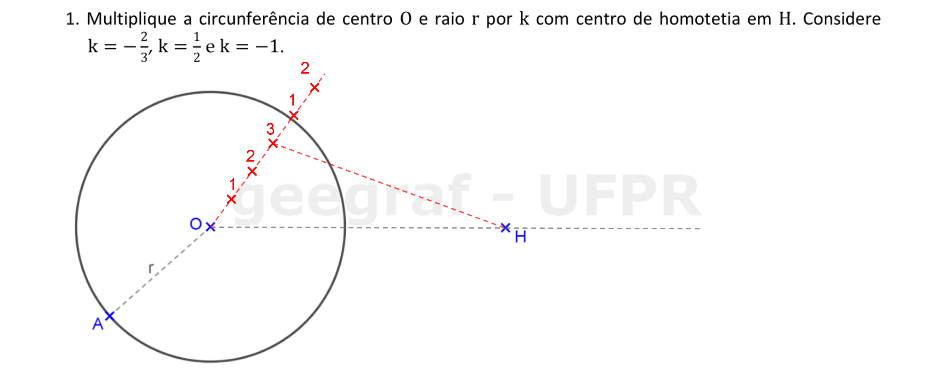
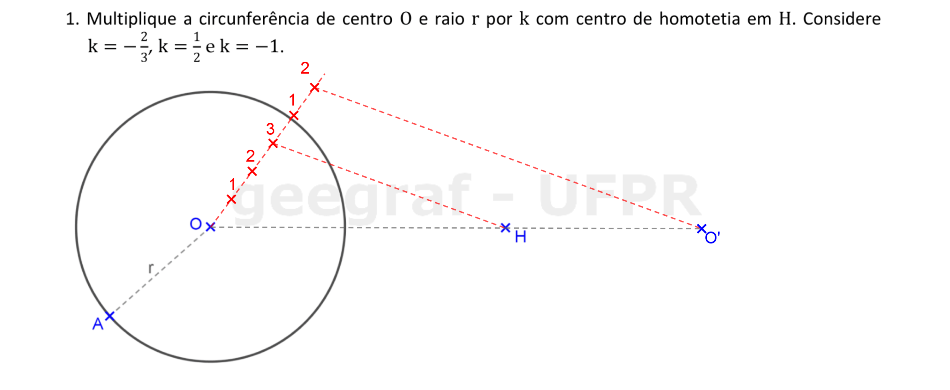
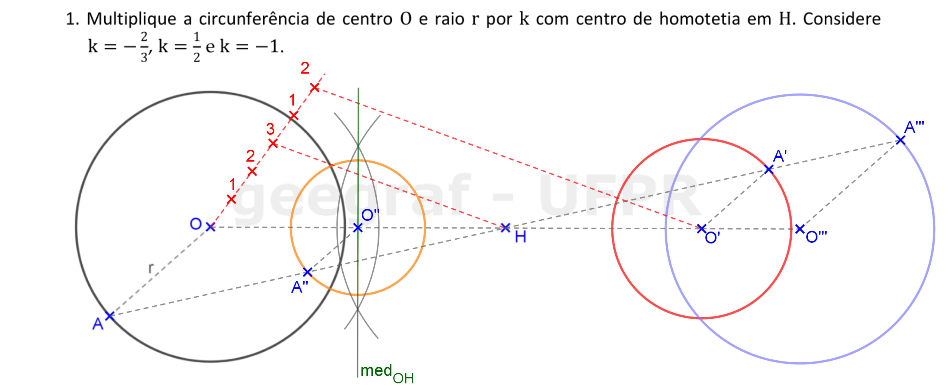
📏 📐 Resolução
Vamos usar a Homotetia para multiplicar uma circunferência, usando o centro de homotetia H e as razões indicadas.


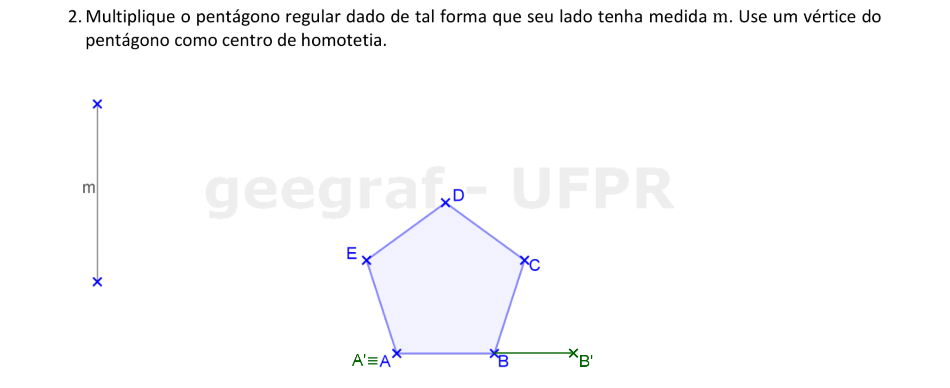
📏 📐 Resolução
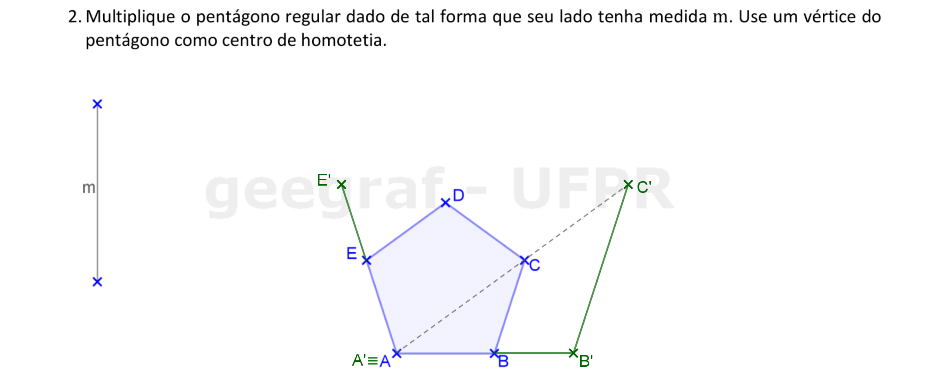
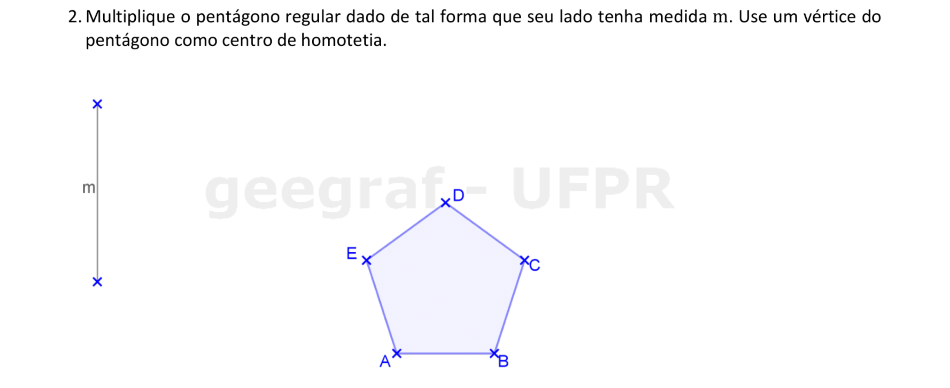
Vamos usar a Homotetia para construir um pentágono regular com medida do lado m.
📏 📐 Resolução
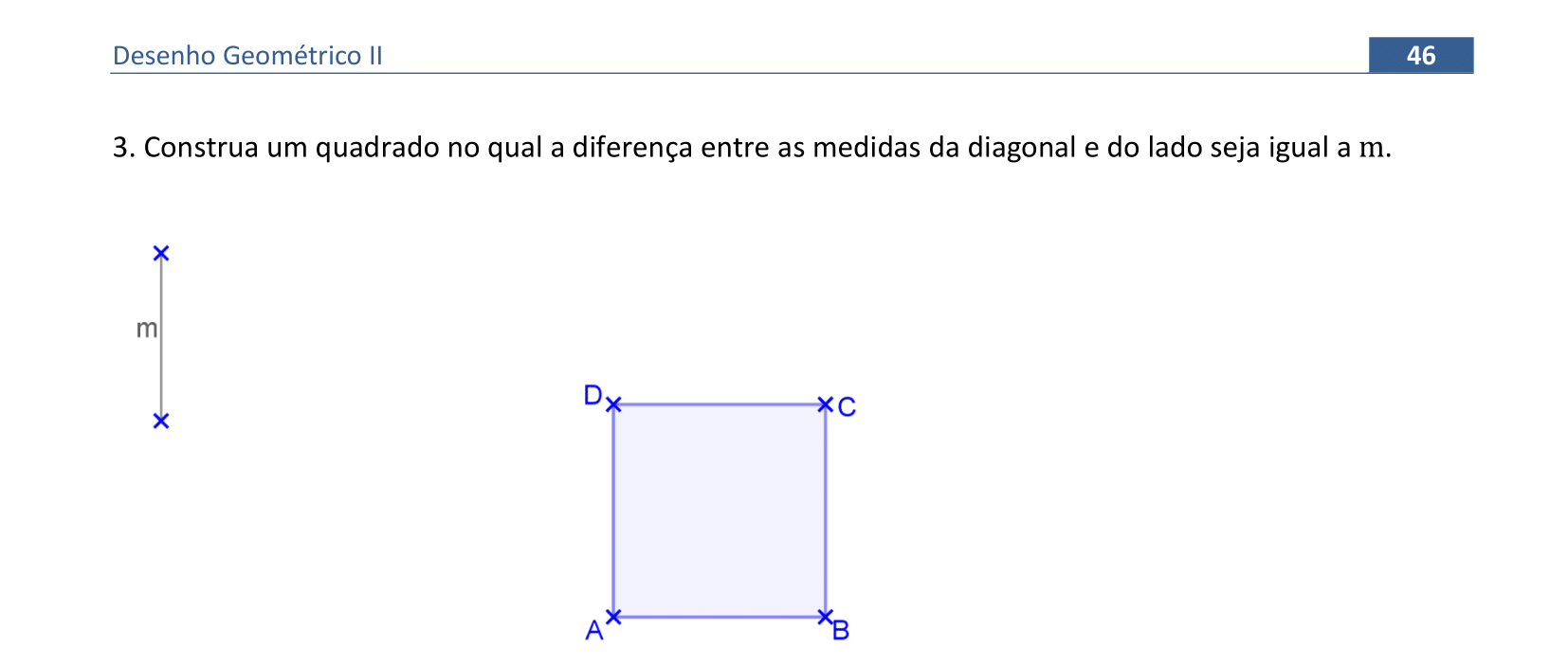
Vamos usar a Homotetia para construir um quadrado com a diferença de medidas entre a diagonal e o lado igual a m.


📏 📐 Resolução
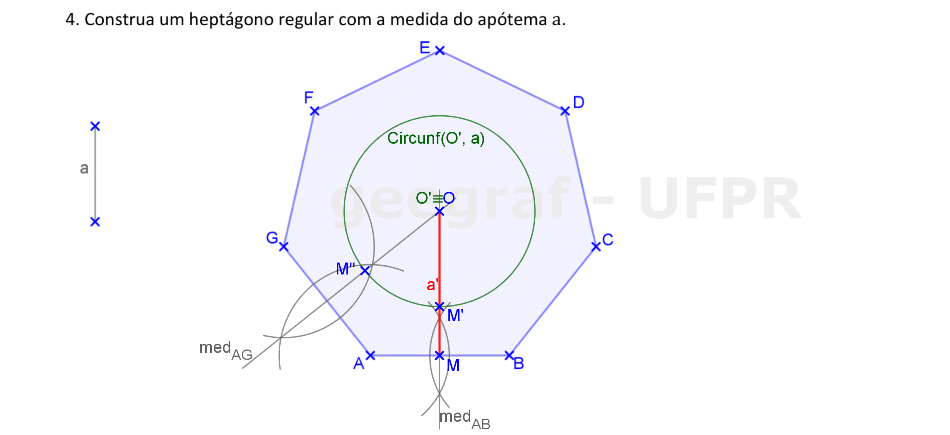
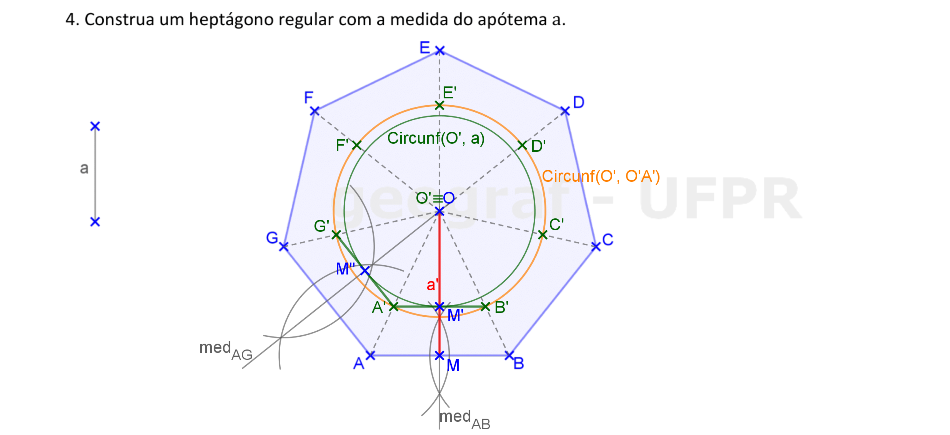
Vamos usar a Homotetia para construir um heptágono regular com a medida do apótema a.


📏 📐 Resolução
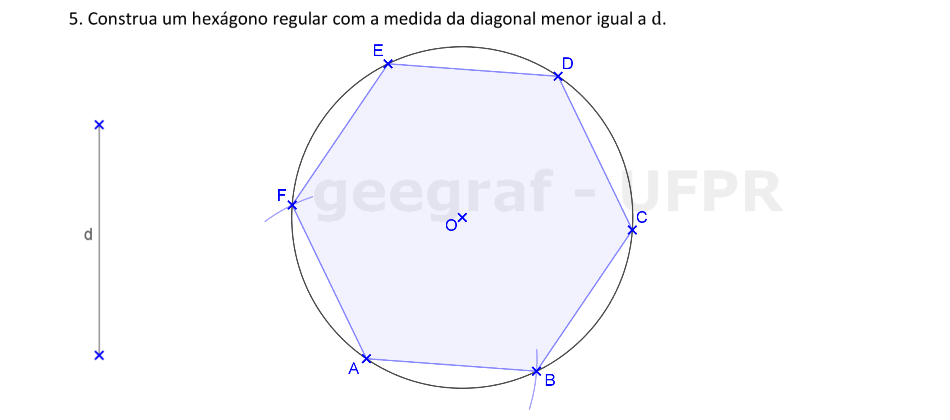
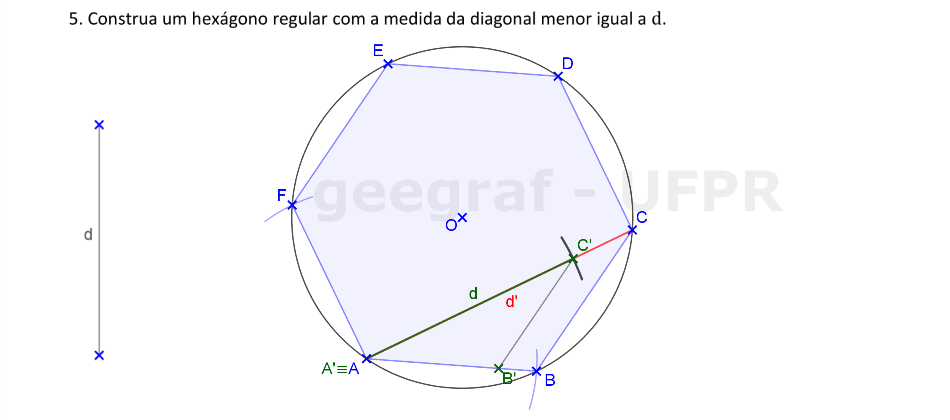
Vamos usar a Homotetia para construir um hexágono regular com a medida da diagonal menor igual a d.

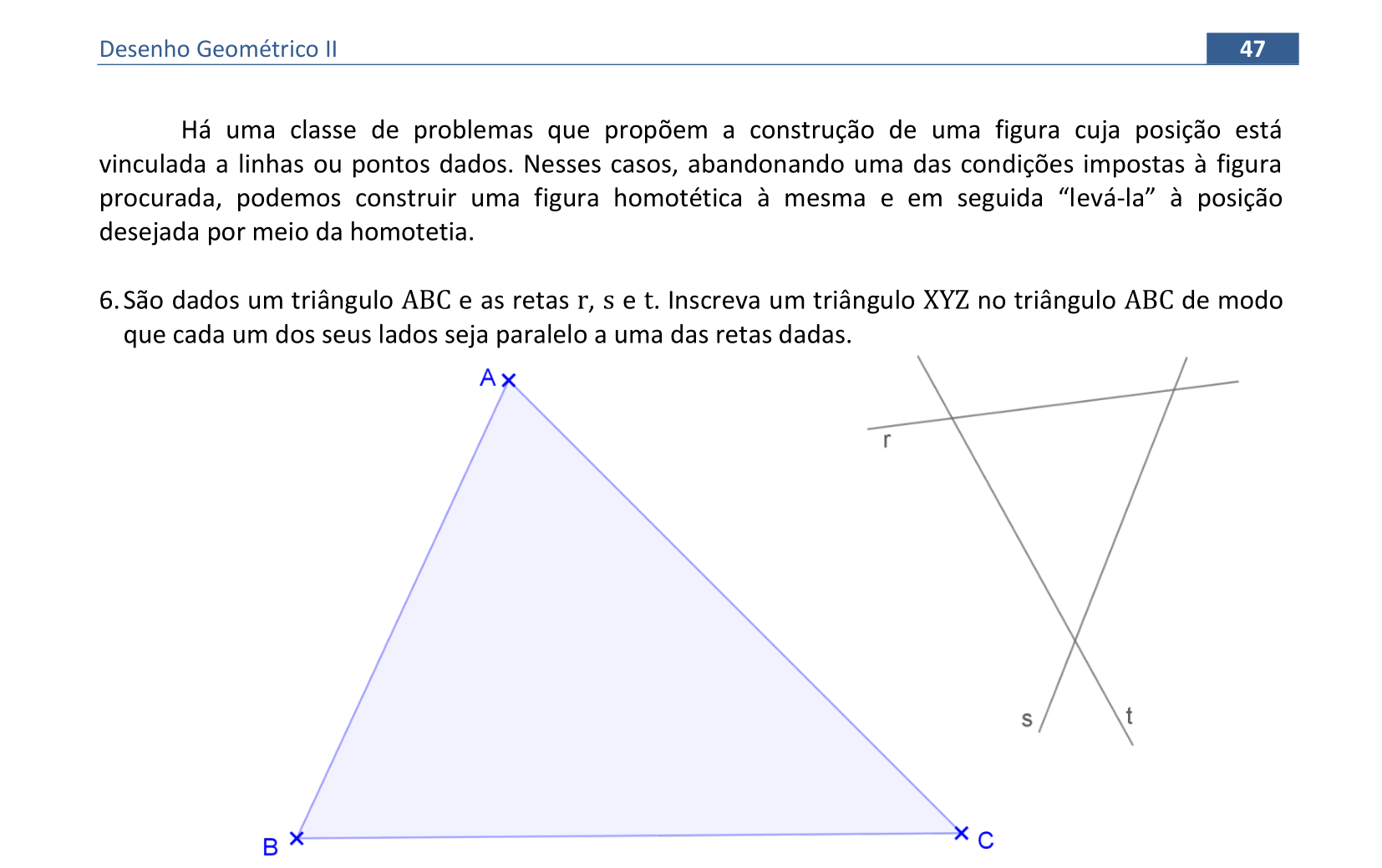
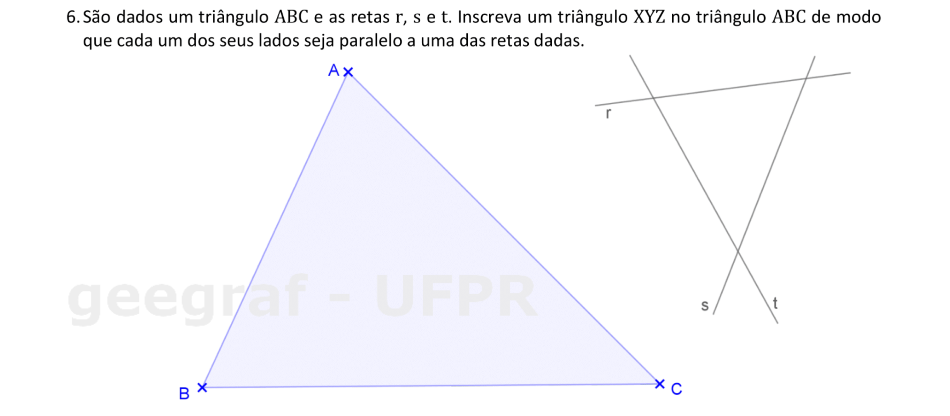
📏 📐 Resolução
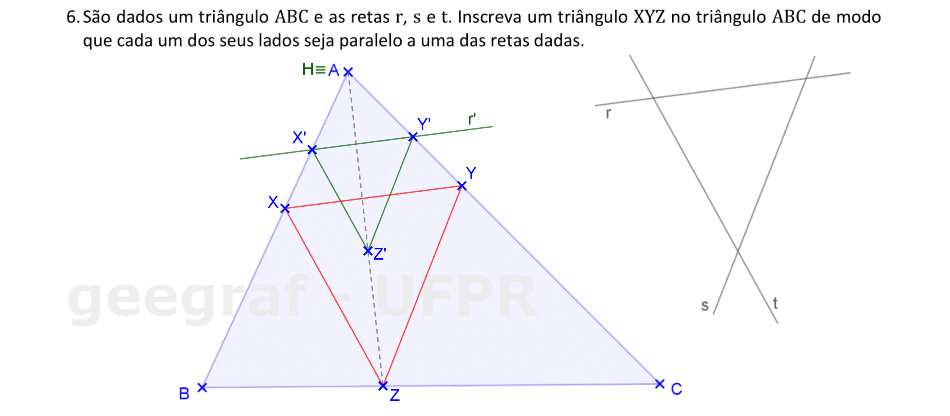
Usaremos a Homotetia para construir um triângulo inscrito no triângulo △ABC.

📏 📐 Resolução
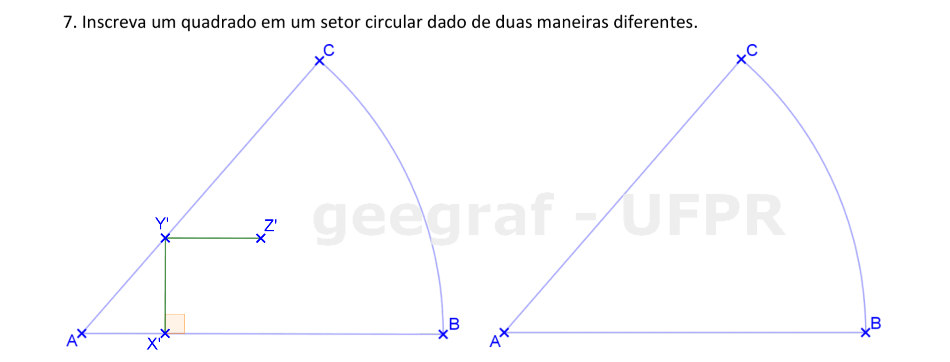
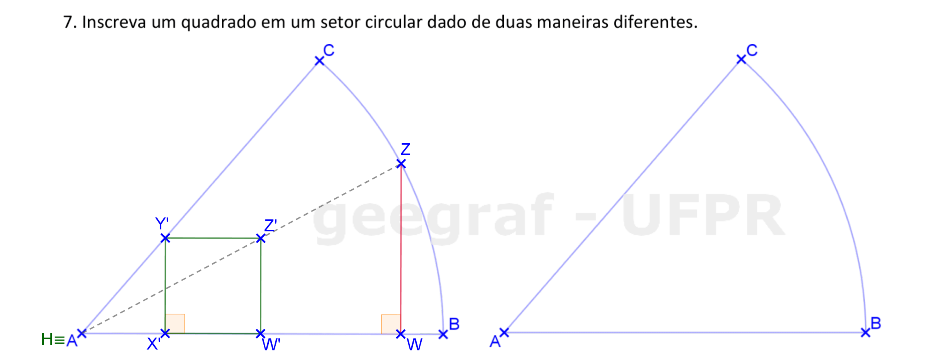
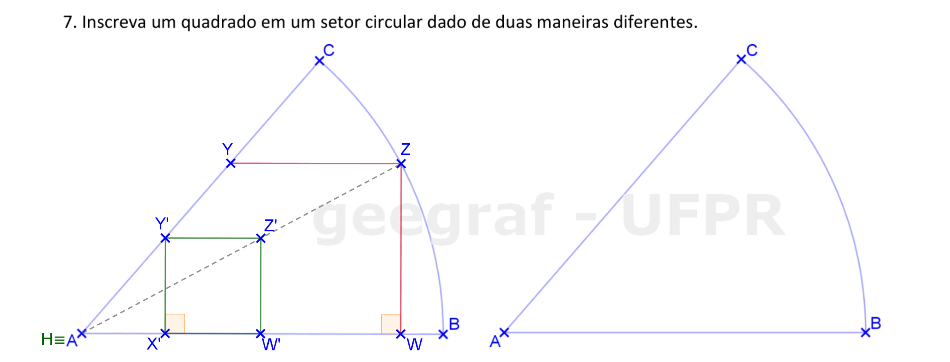
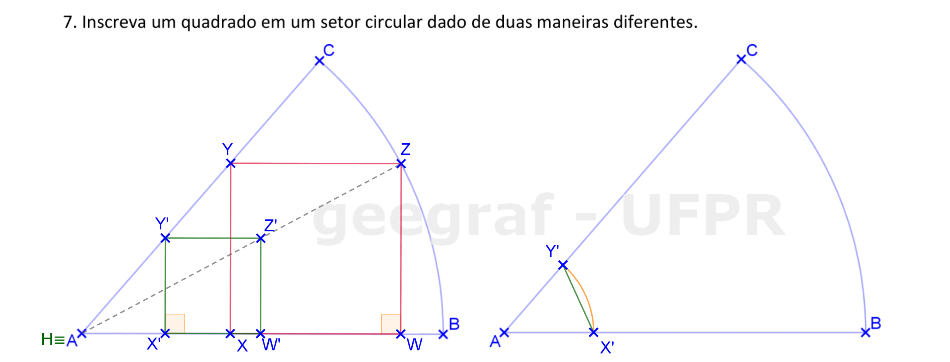
Usaremos a Homotetia para construir um quadrado inscrito em um setor circular.

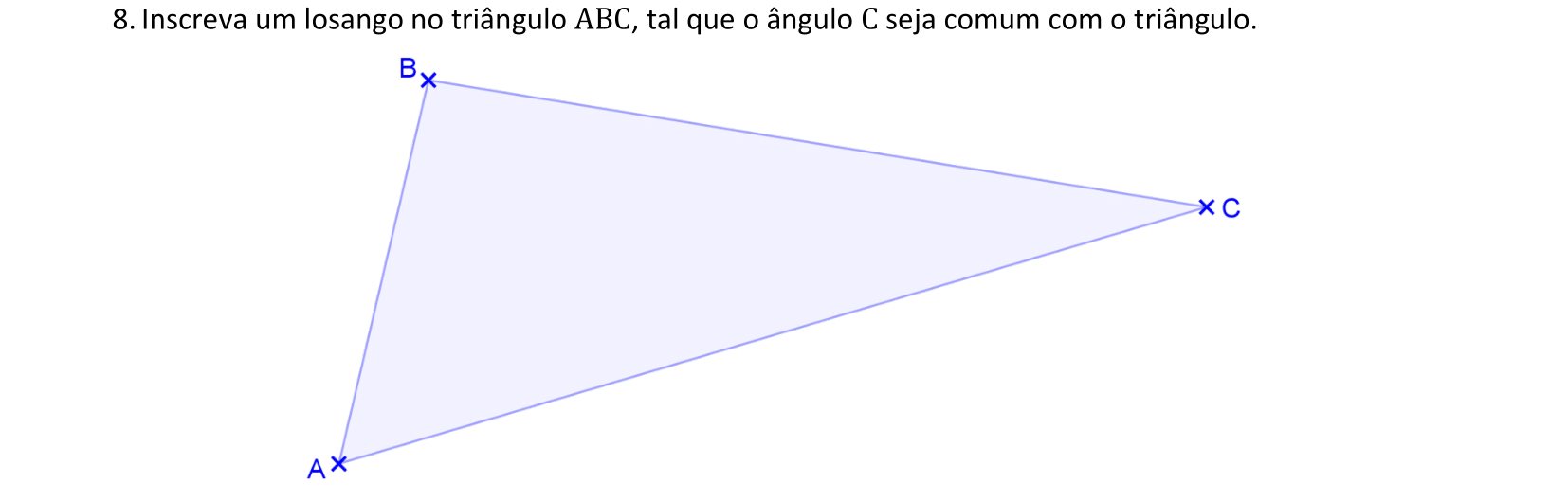
📏 📐 Resolução
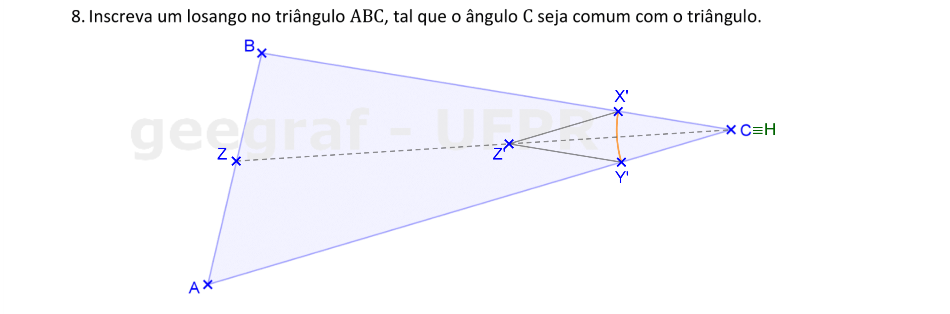
Usaremos a Homotetia para construir um losango inscrito no triângulo △ABC.


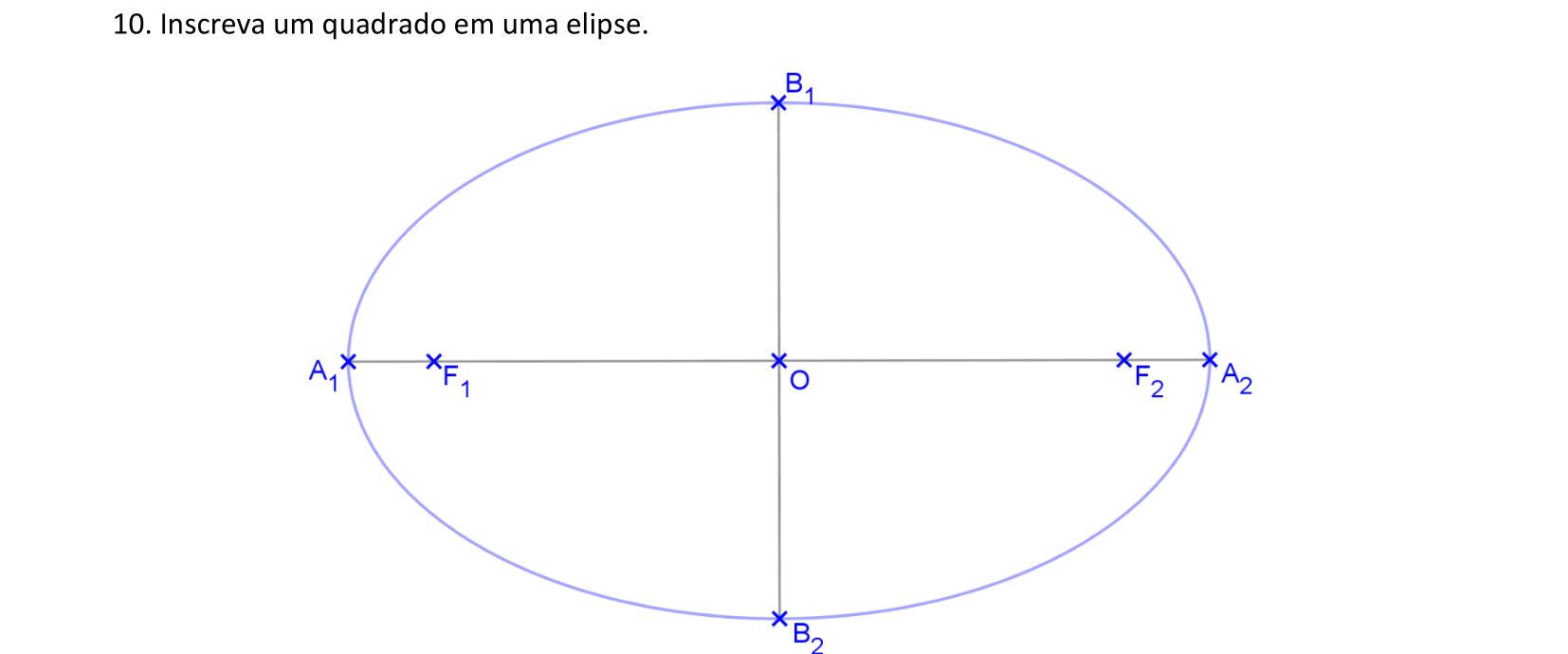
📏 📐 Resolução
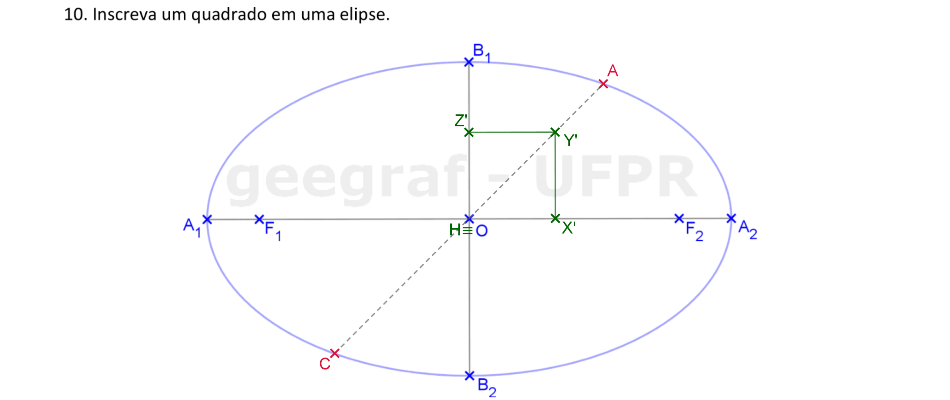
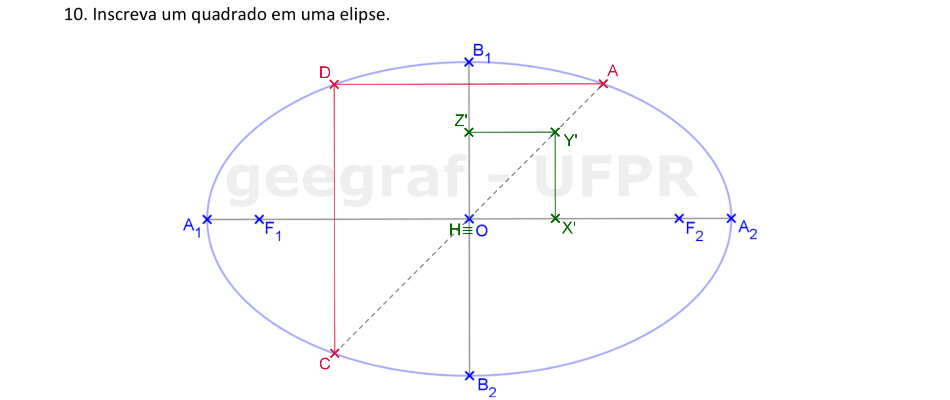
Usaremos a Homotetia para construir um quadrado inscrito em uma elipse.
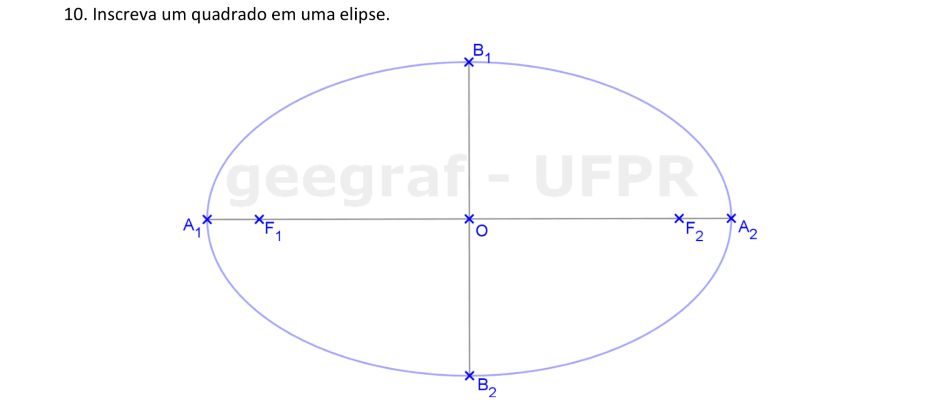
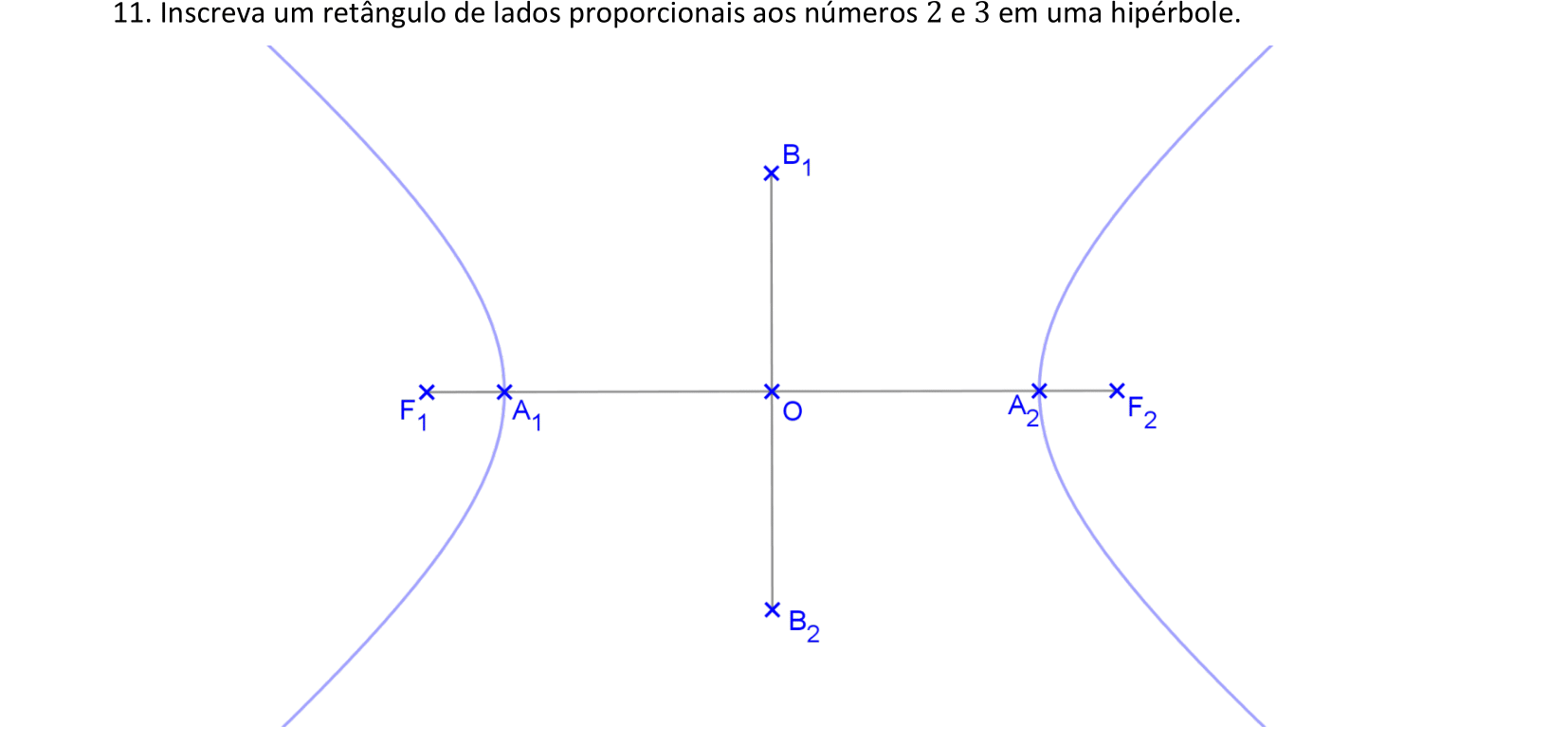
📏 📐 Resolução
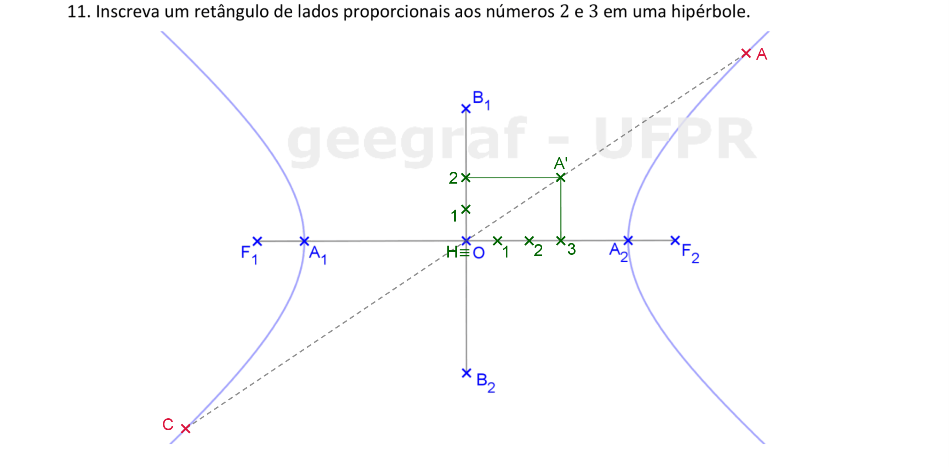
Usaremos a Homotetia para construir um retângulo inscrito em uma hipérbole.


📏 📐 Resolução
Usaremos a Homotetia para construir um triângulo equilátero inscrito em uma parábola.


📏 📐 Resolução
Vamos construir uma espiral de Arquimedes por pontos. Usaremos 8 pontos neste exemplo.


📏 📐 Resolução
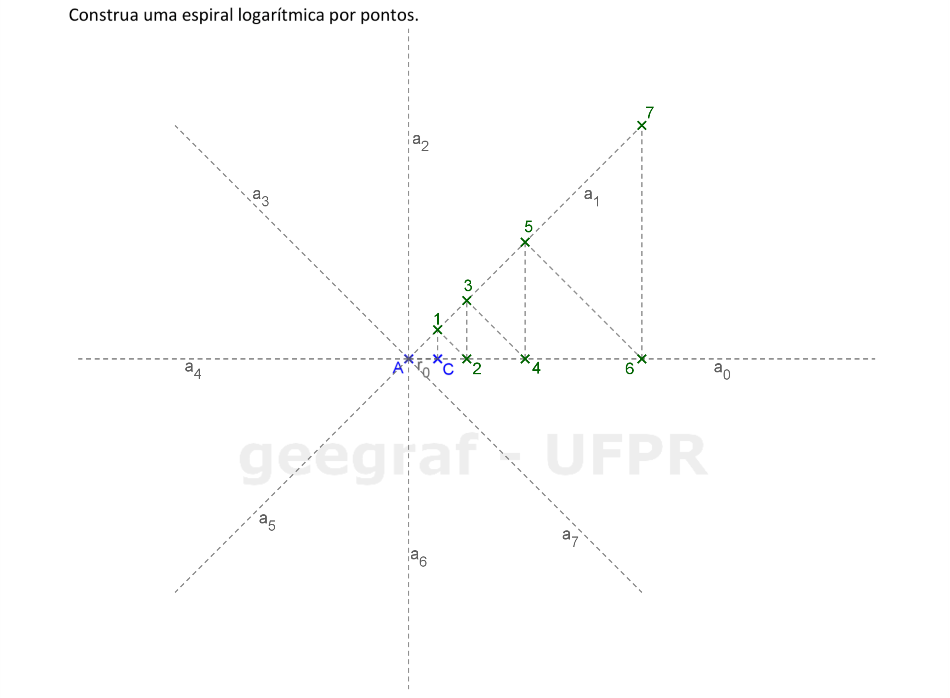
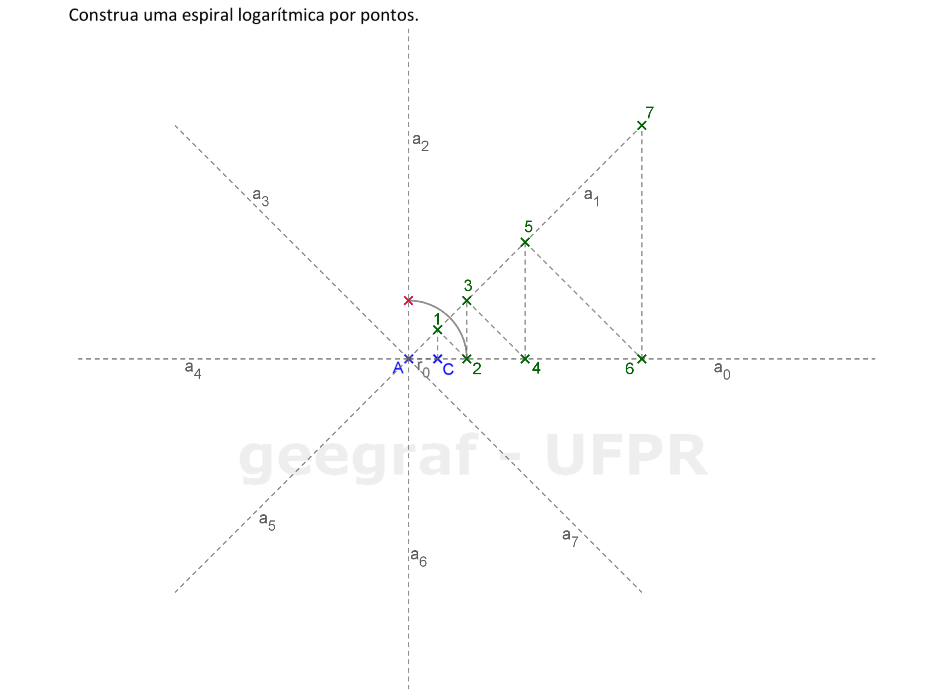
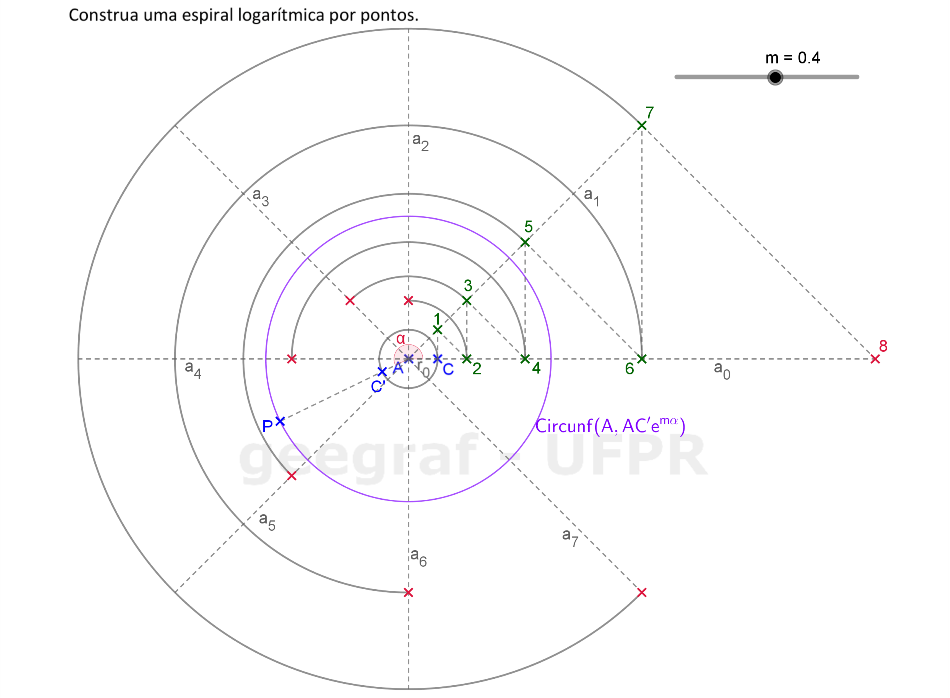
Vamos construir uma espiral logarítmica por pontos. Usaremos 8 pontos neste exemplo.
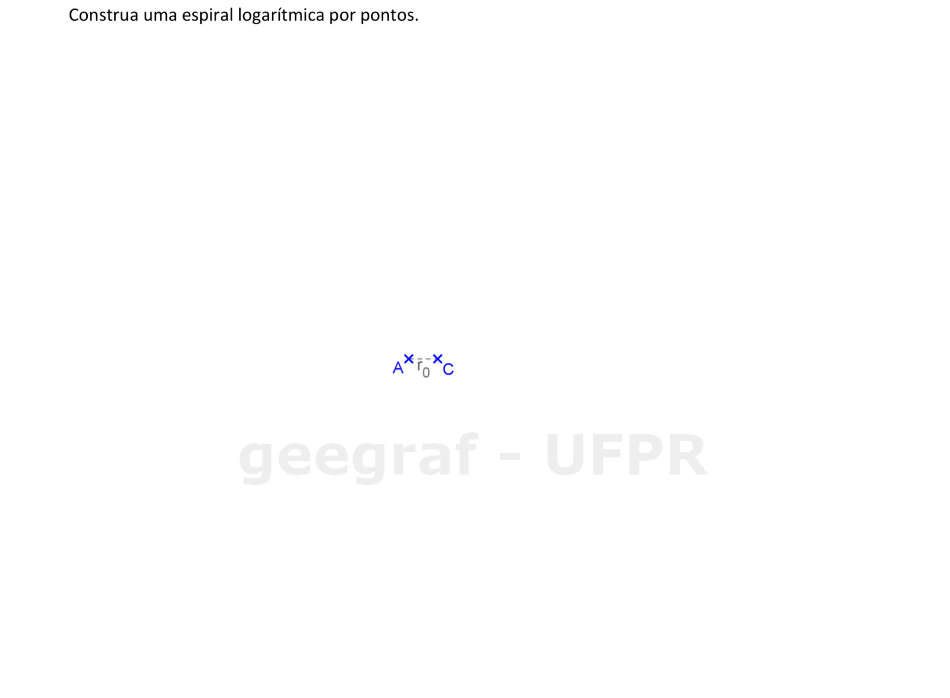
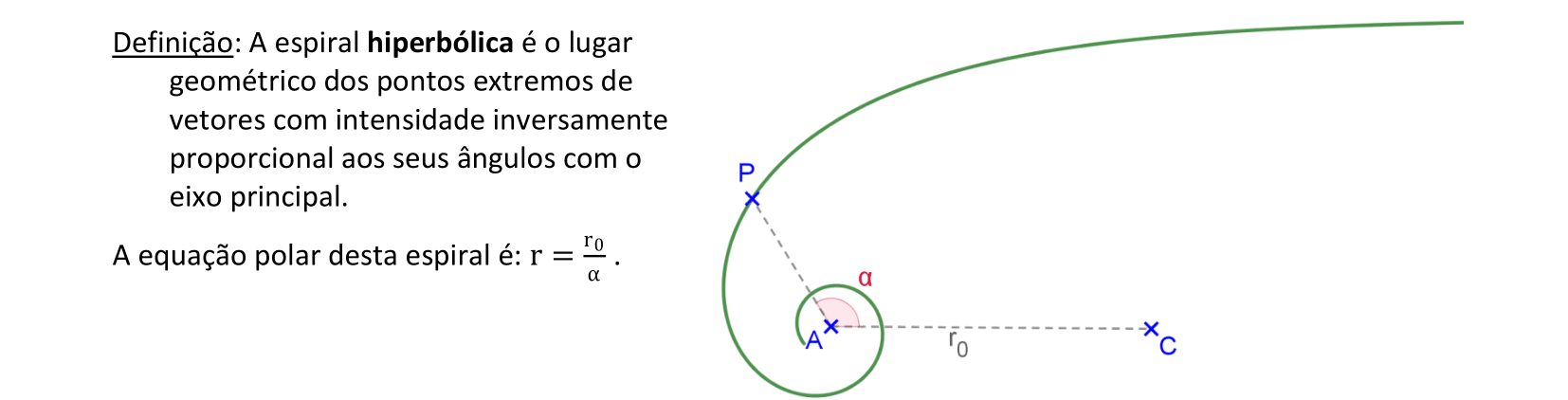

📏 📐 Resolução
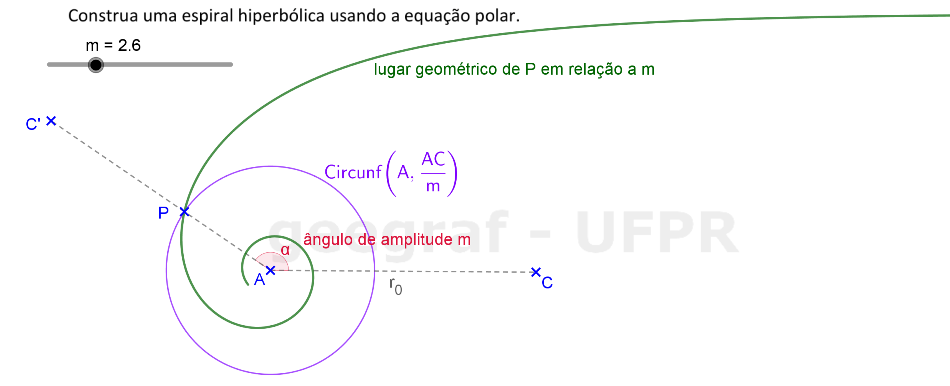
Vamos construir uma espiral hiperbólica usando sua equação polar.


📏 📐 Resolução
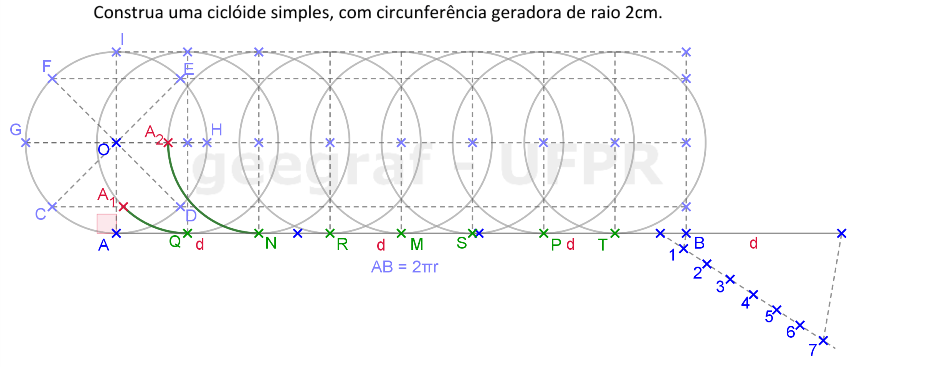
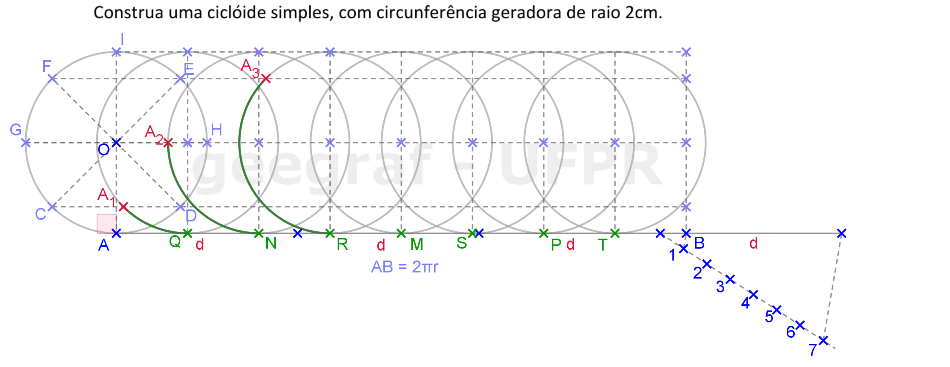
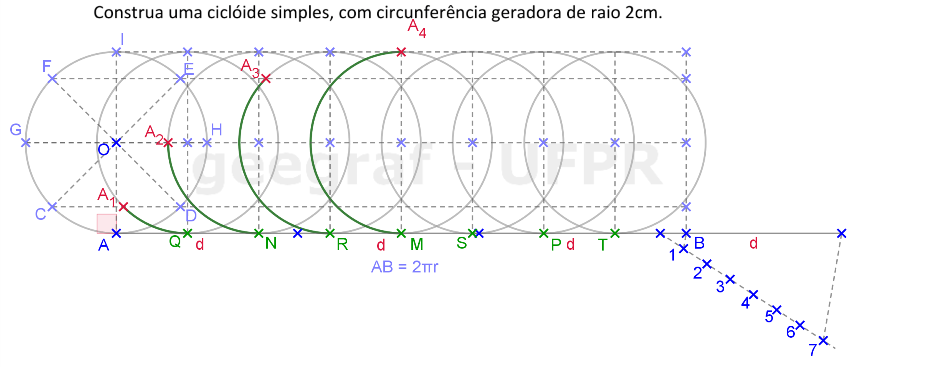
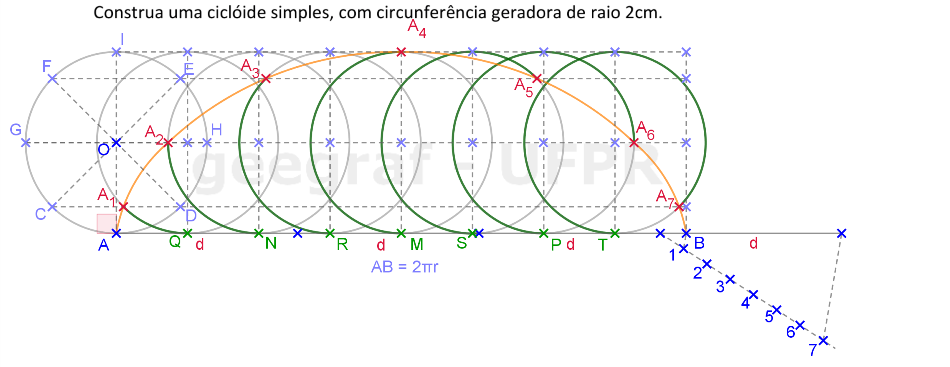
Vamos construir uma ciclóide simples, por pontos, usando uma circunferência geradora com raio de medida igual a 2cm.



📏 📐 Resolução
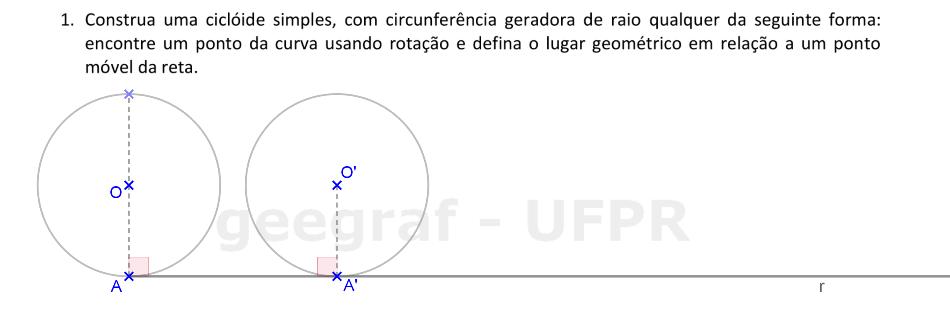
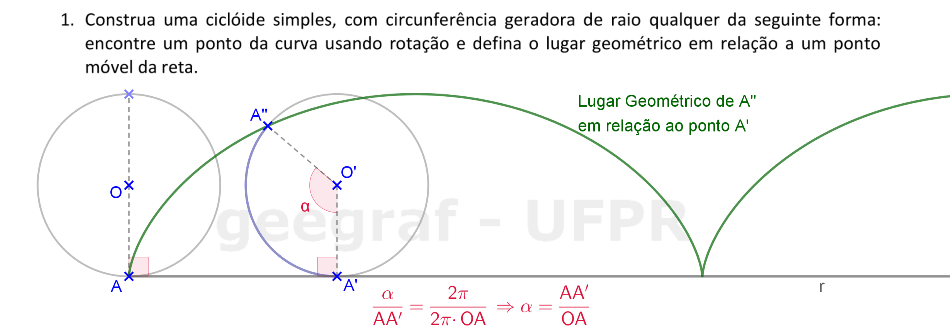
Vamos construir uma ciclóide usando uma rotação.


📏 📐 Resolução
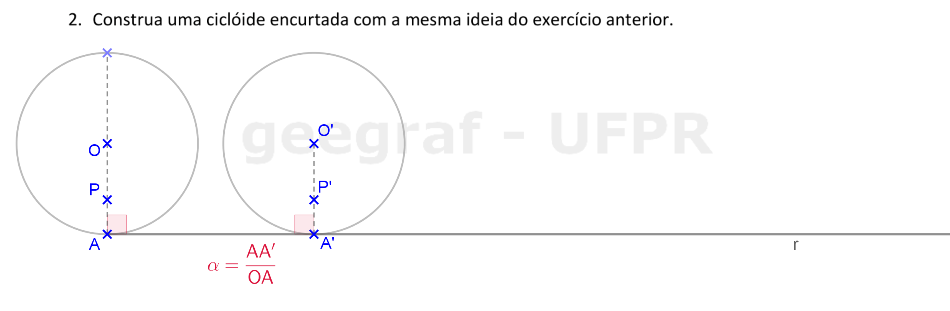
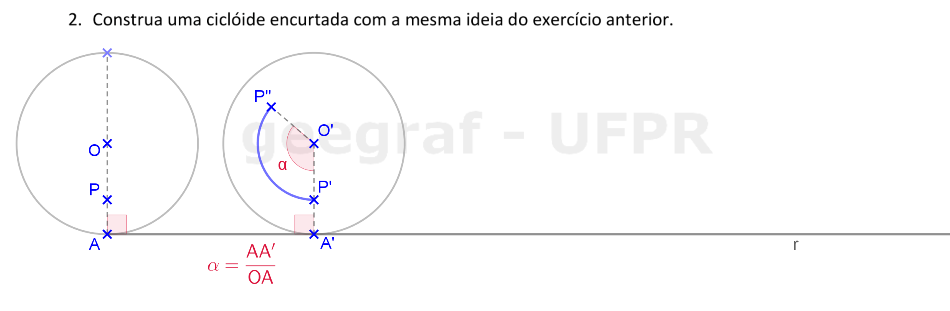
Vamos construir uma ciclóide encurtada usando uma rotação.



📏 📐 Resolução
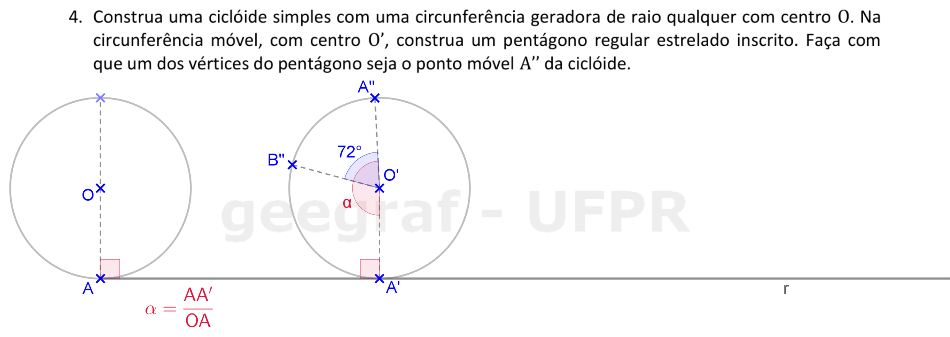
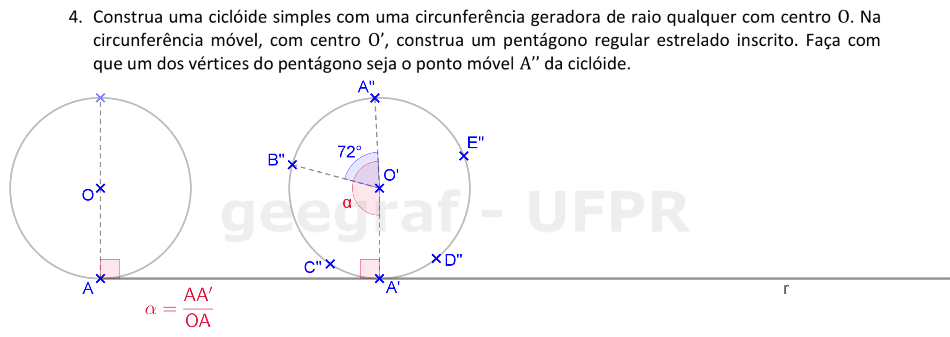
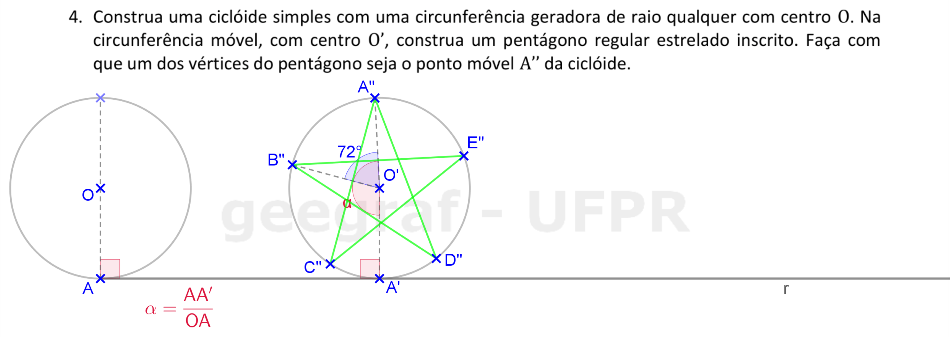
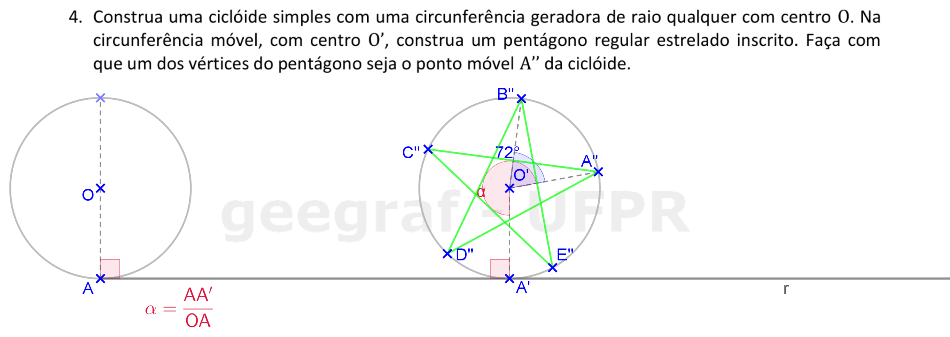
Vamos construir uma ciclóide usando uma rotação, com um pentágono regular estrelado giratório.



📏 📐 Resolução
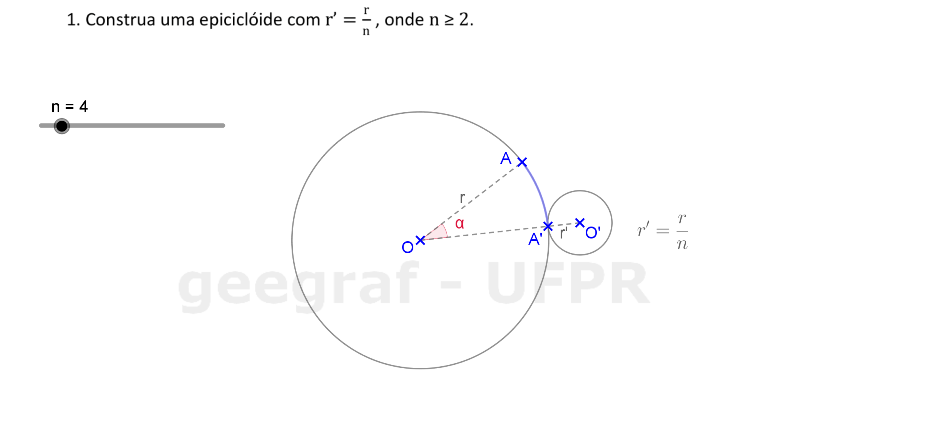
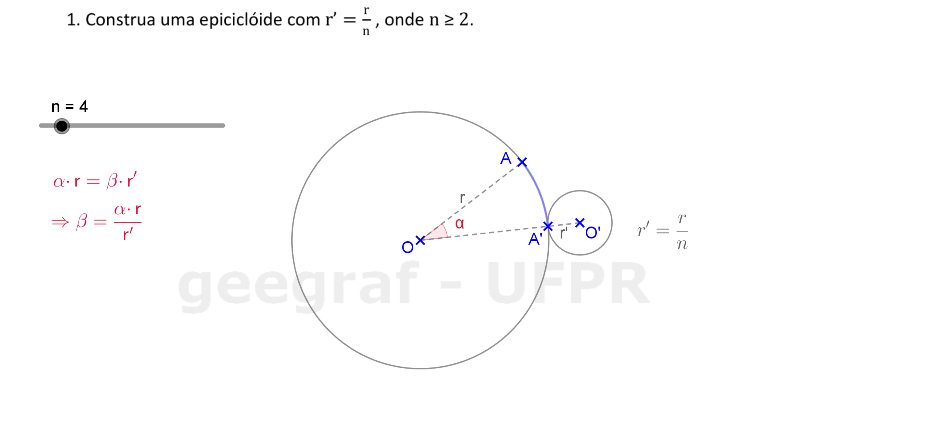
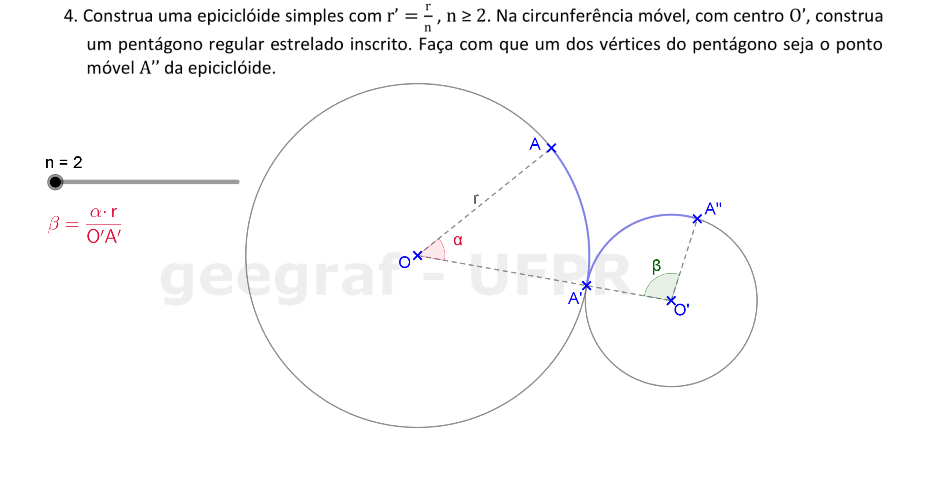
Vamos construir uma epiciclóide usando rotações.

📏 📐 Resolução
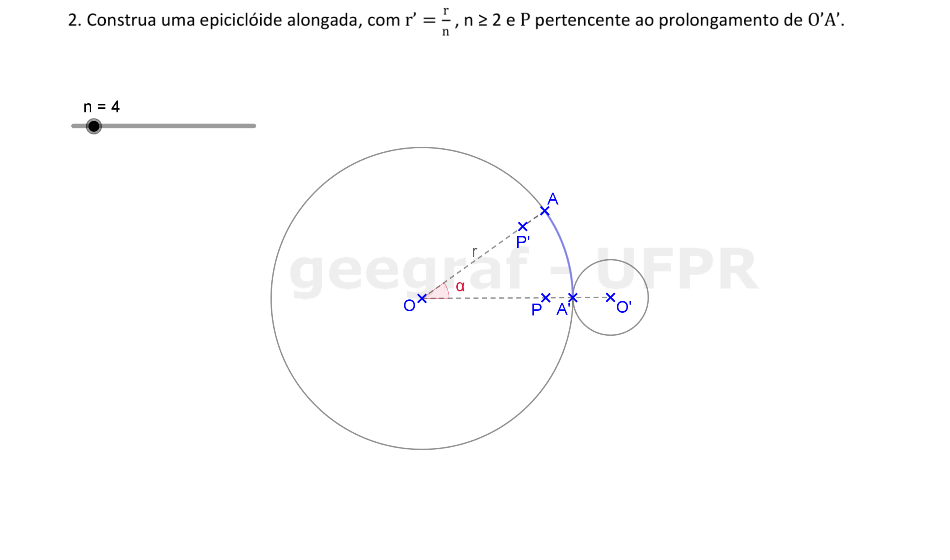
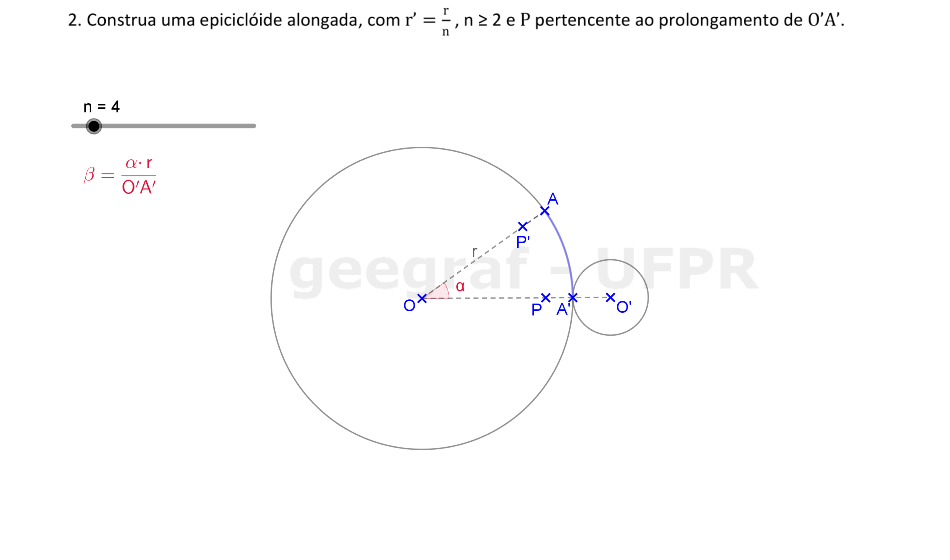
Vamos construir uma epiciclóide alongada usando rotações.



📏 📐 Resolução
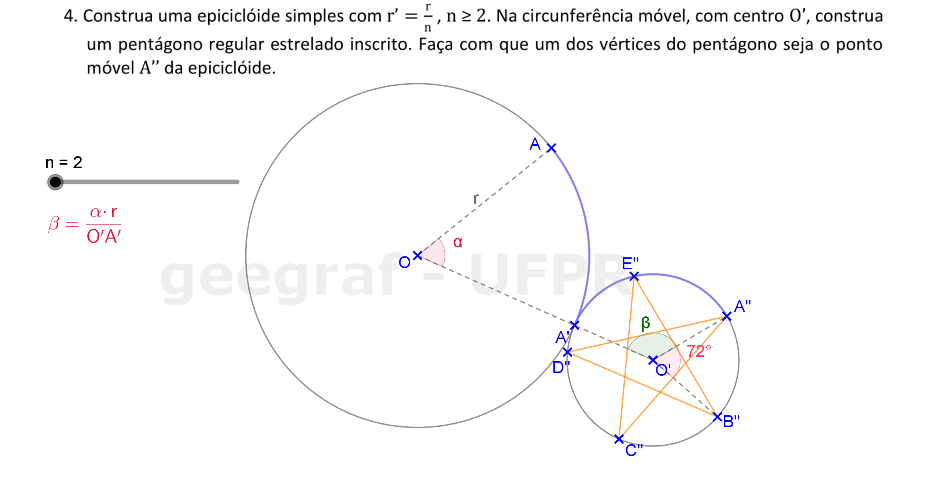
Vamos construir uma epiciclóide usando rotações, com um pentágono regular estrelado giratório.


📏 📐 Resolução
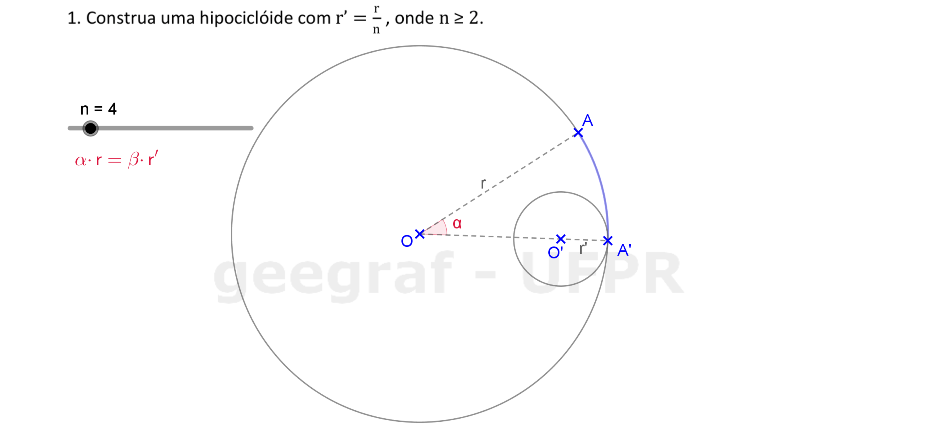
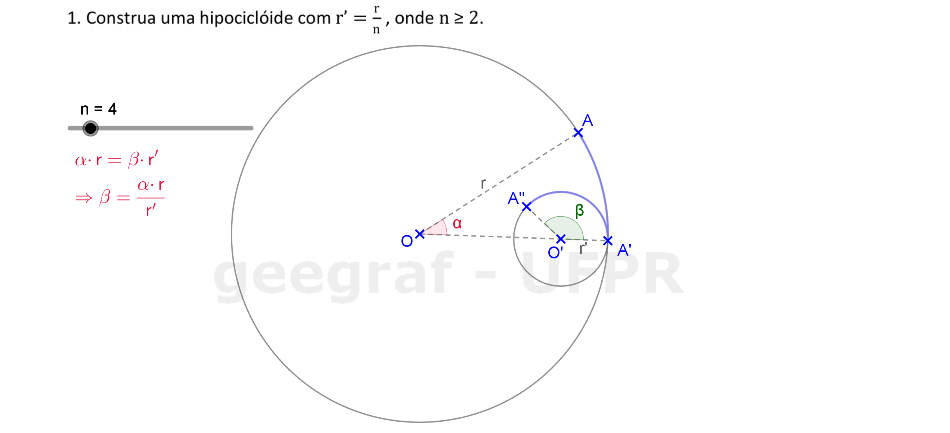
Vamos construir uma hipociclóide usando rotações.

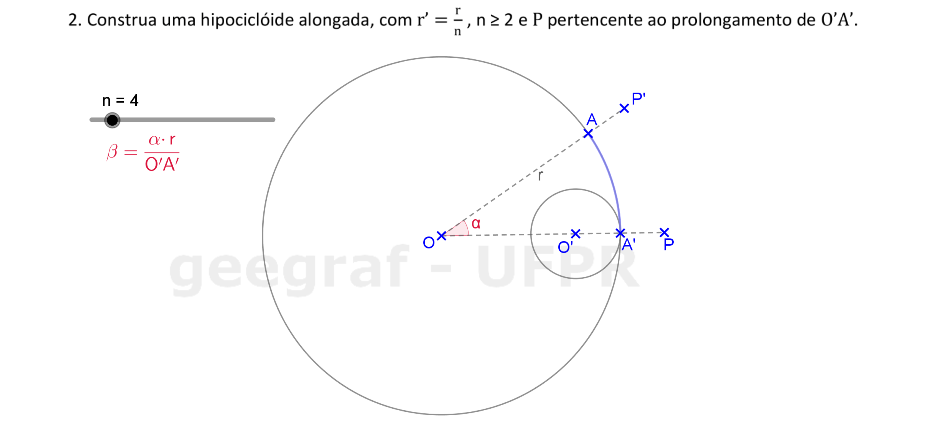
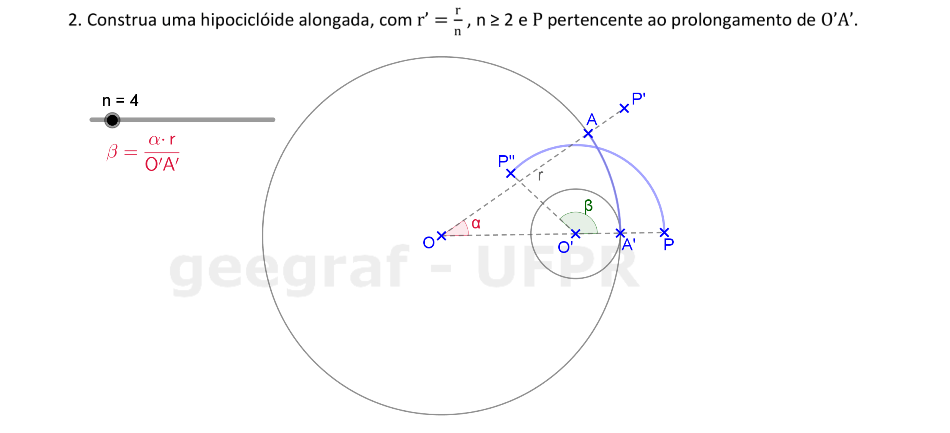
📏 📐 Resolução
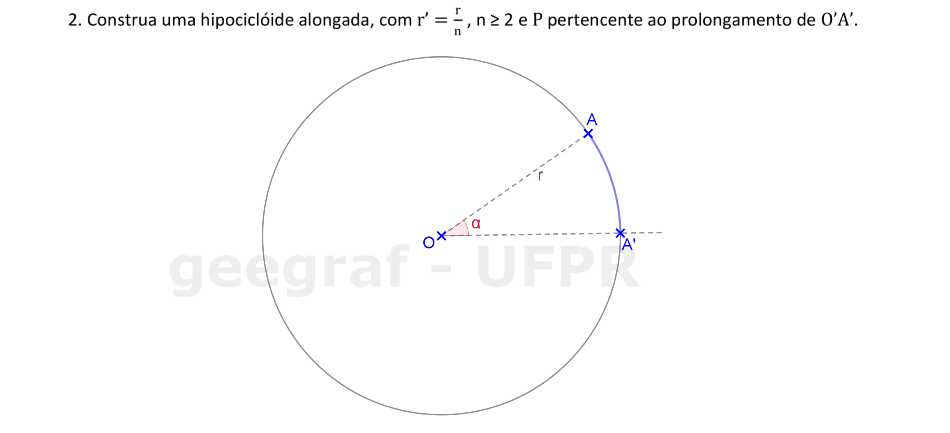
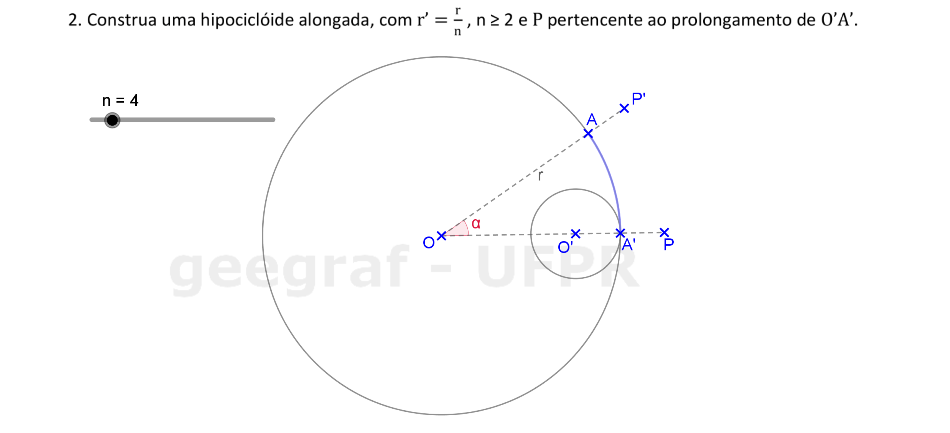
Vamos construir uma hipociclóide alongada usando rotações.

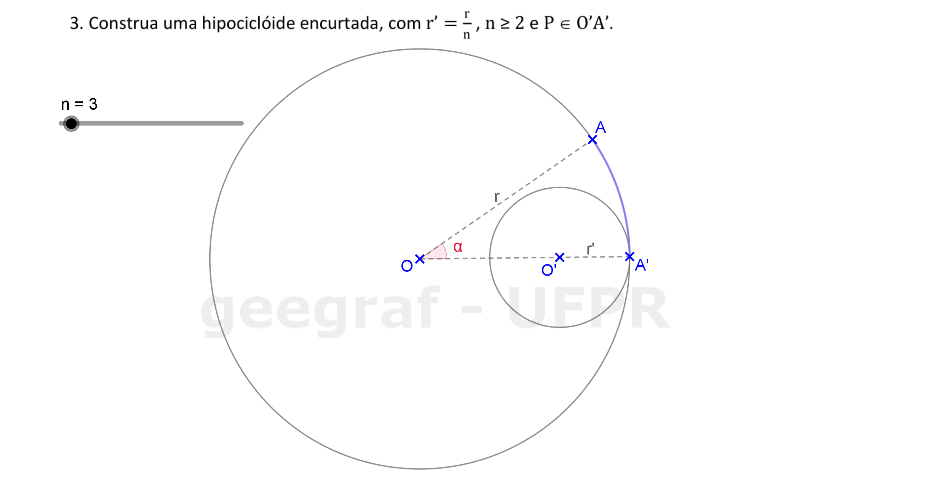
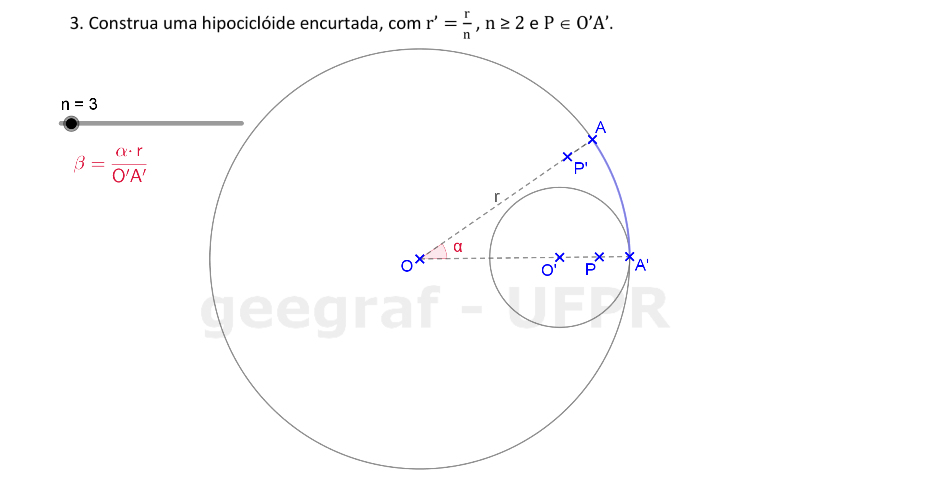
📏 📐 Resolução
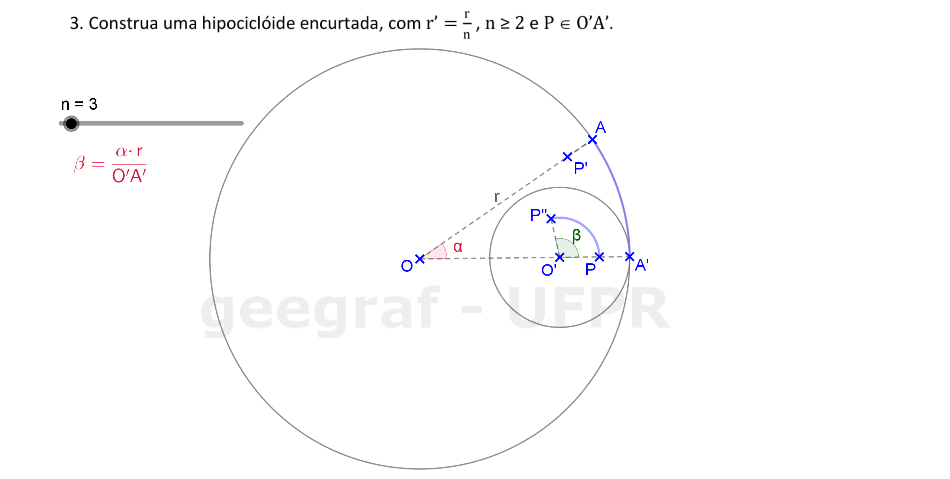
Vamos construir uma hipociclóide encurtada usando rotações.


📏 📐 Resolução
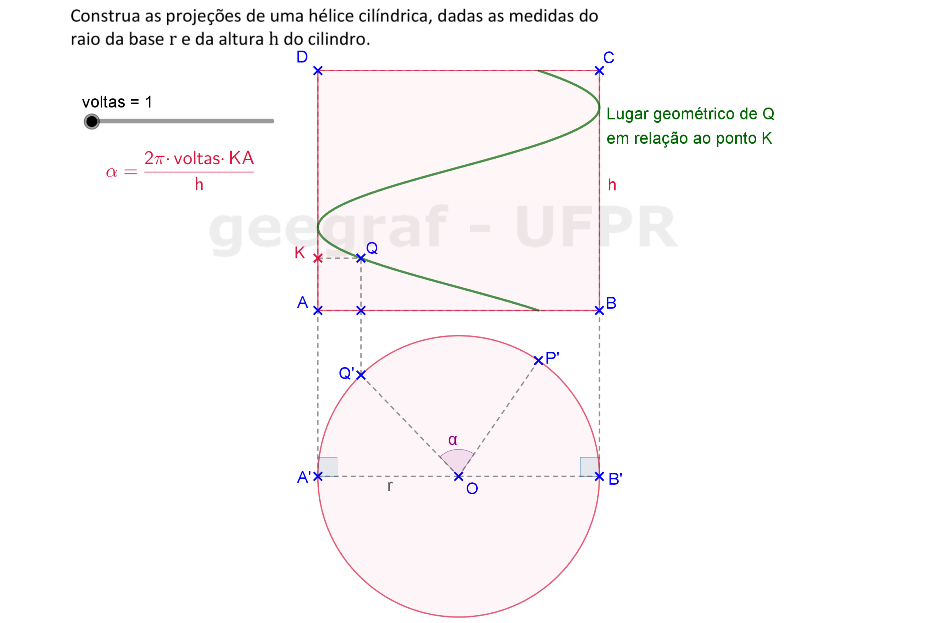
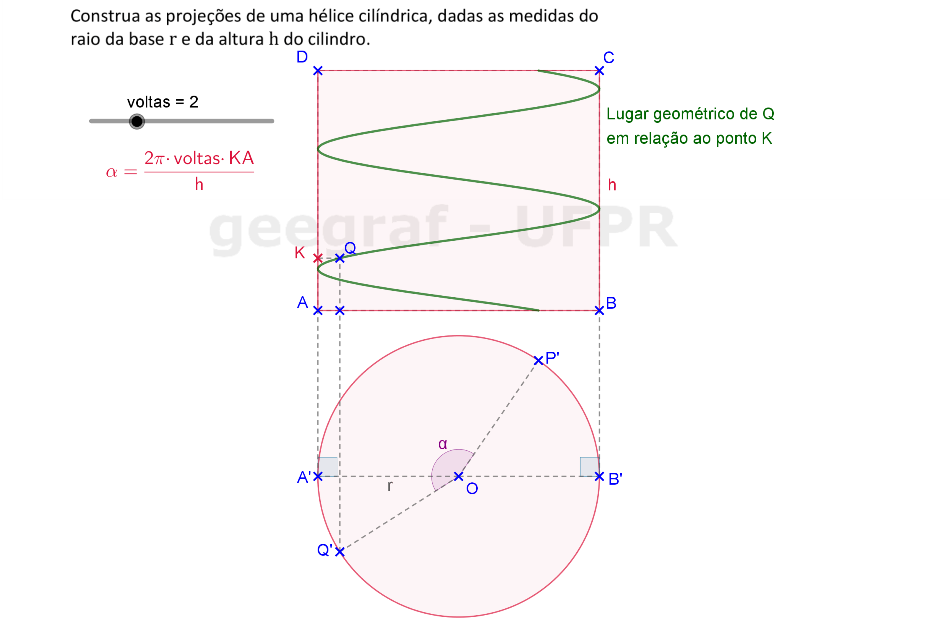
Vamos construir as projeções frontal e superior de uma hélice cilíndrica usando rotações.


📏 📐 Resolução
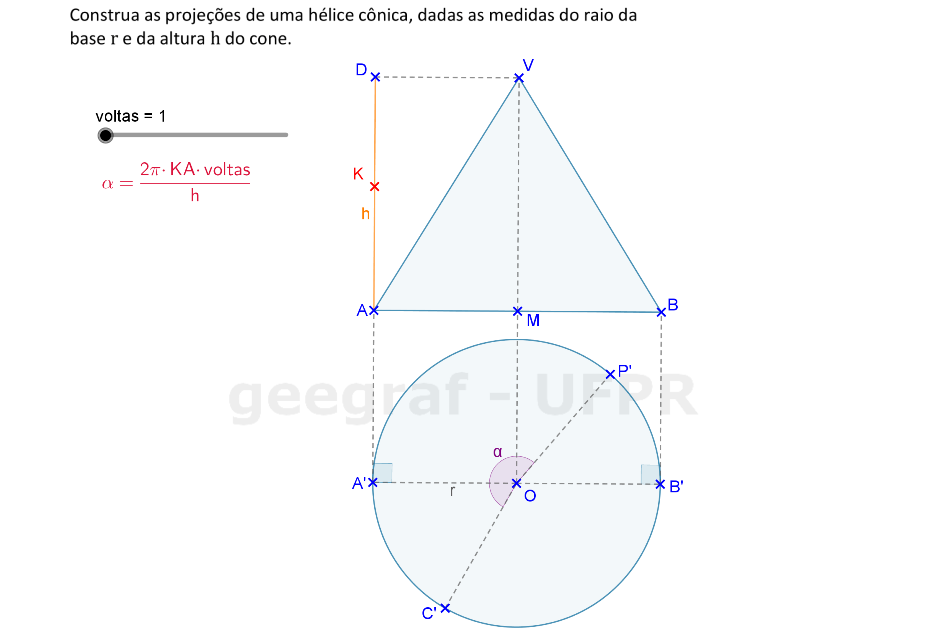
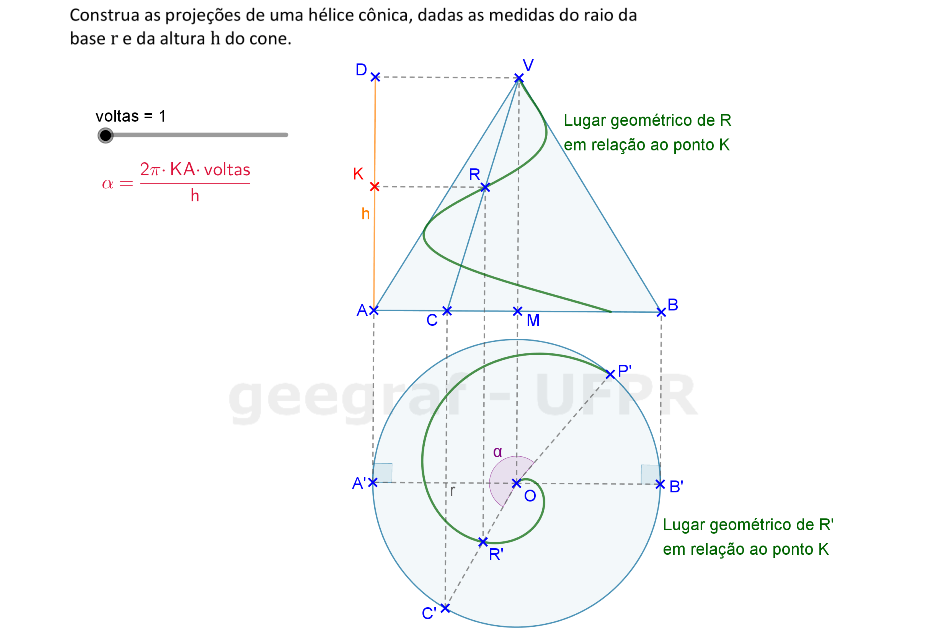
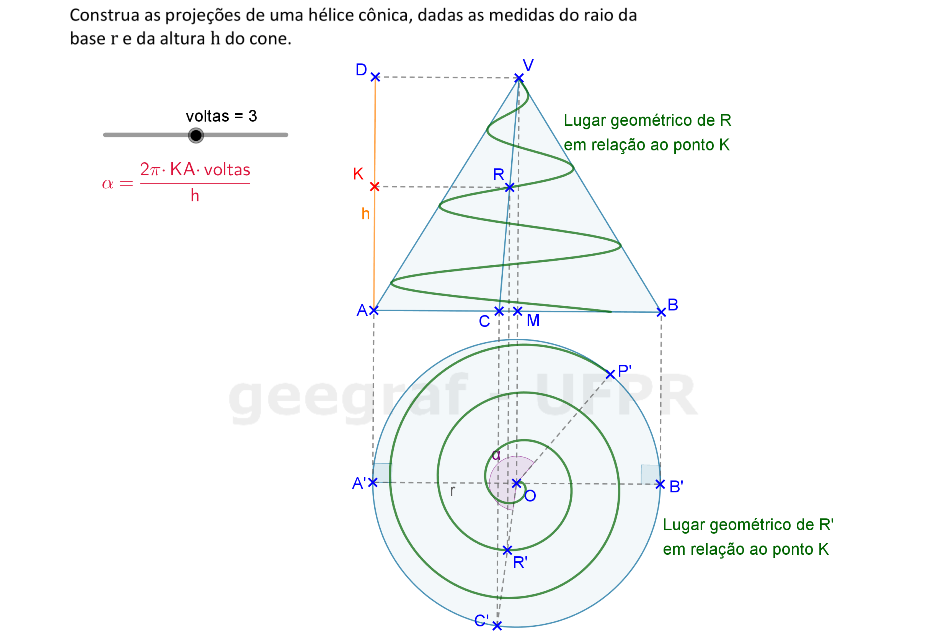
Vamos construir as projeções frontal e superior de uma hélice cônica usando rotações.

5. Translação, Inversão e curvas
Material da página 54 até a página 67.

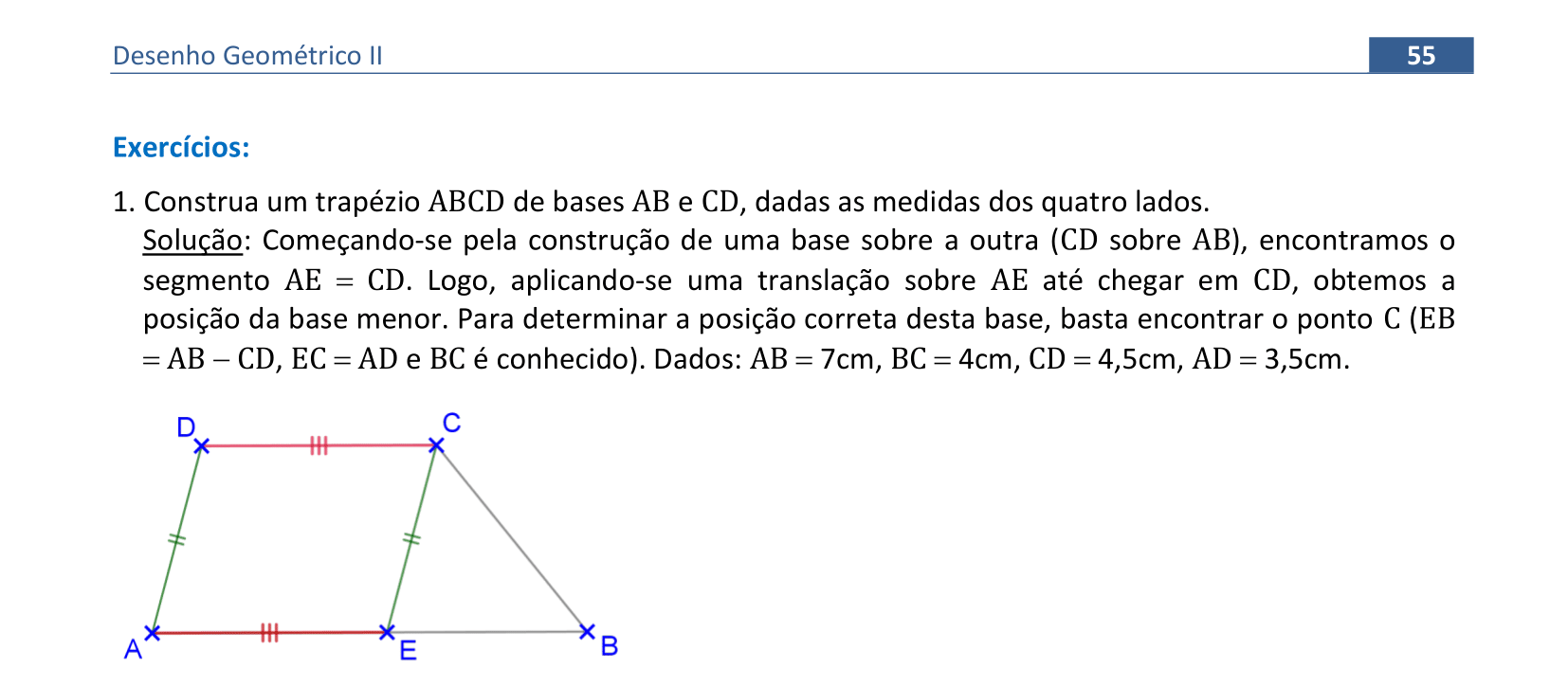
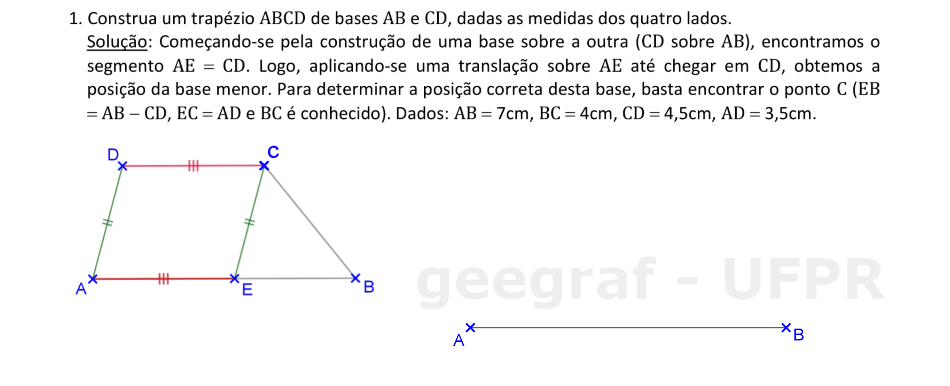
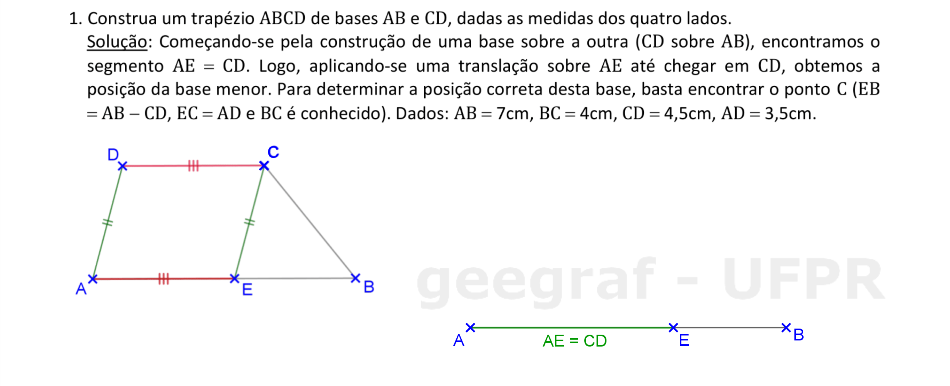
📏 📐 Resolução
Vamos construir o trapézio ABCD, dadas as medidas dos lados.
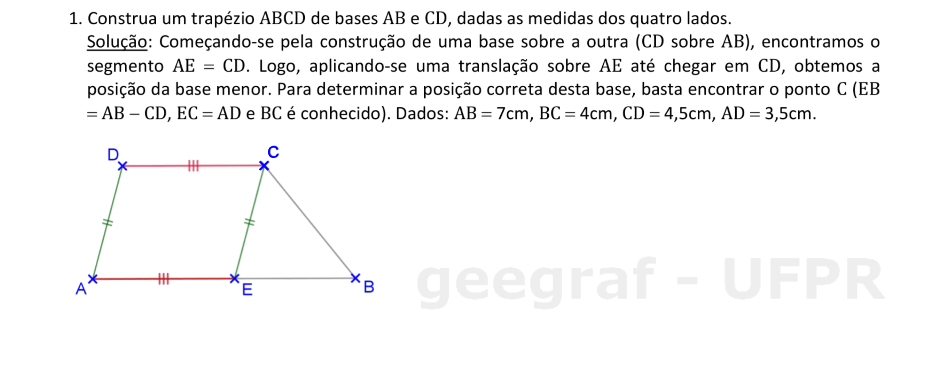

📏 📐 Resolução
Vamos construir o trapézio ABCD, dadas as medidas das bases e das diagonais.

📏 📐 Resolução
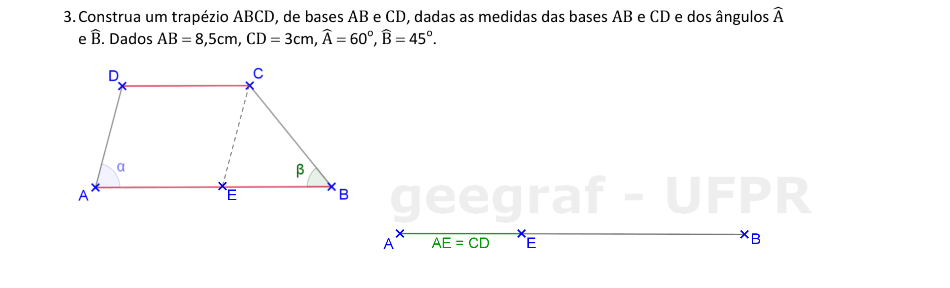
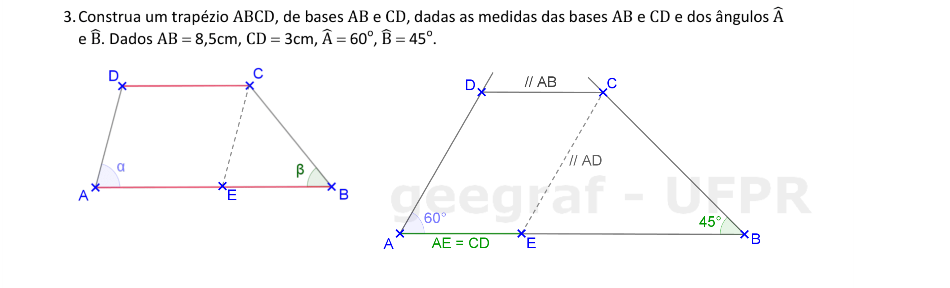
Vamos construir o trapézio ABCD, dadas as medidas das bases e de dois ângulos.

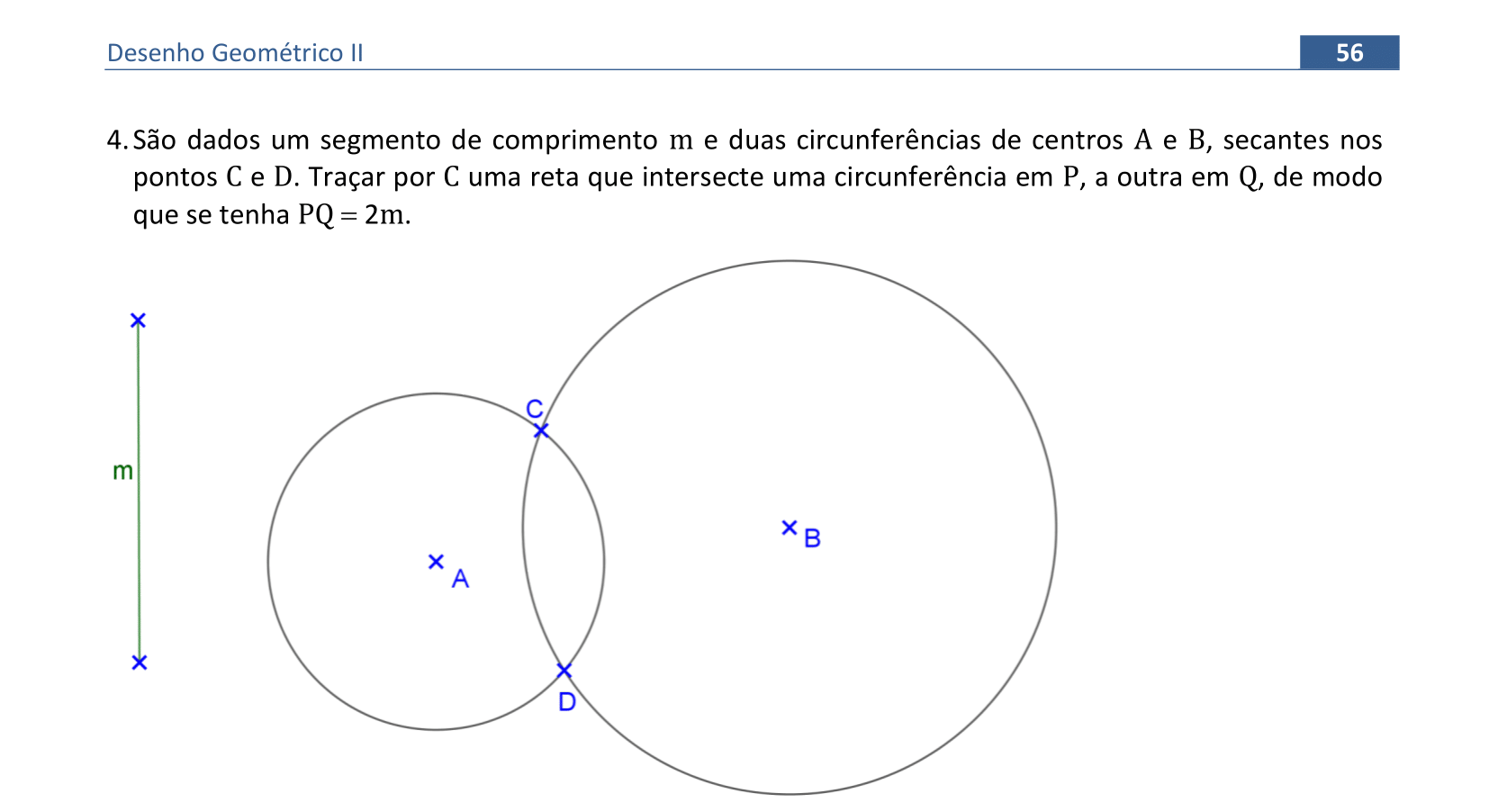
📏 📐 Resolução
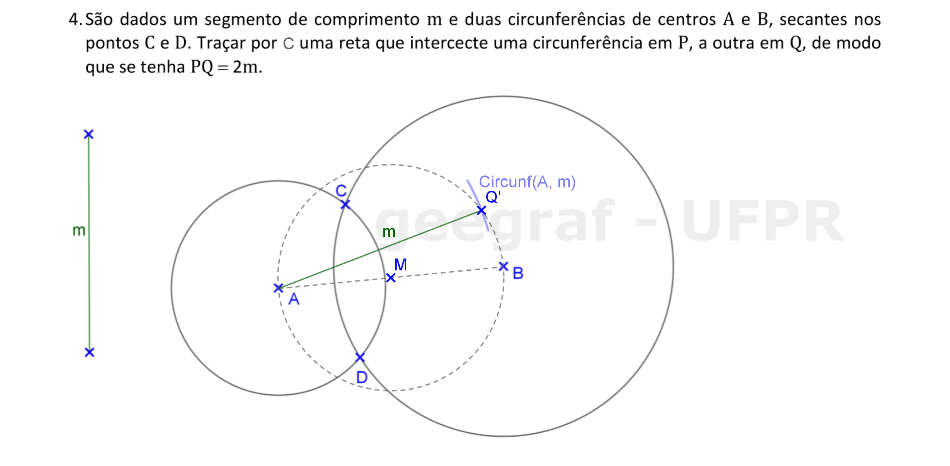
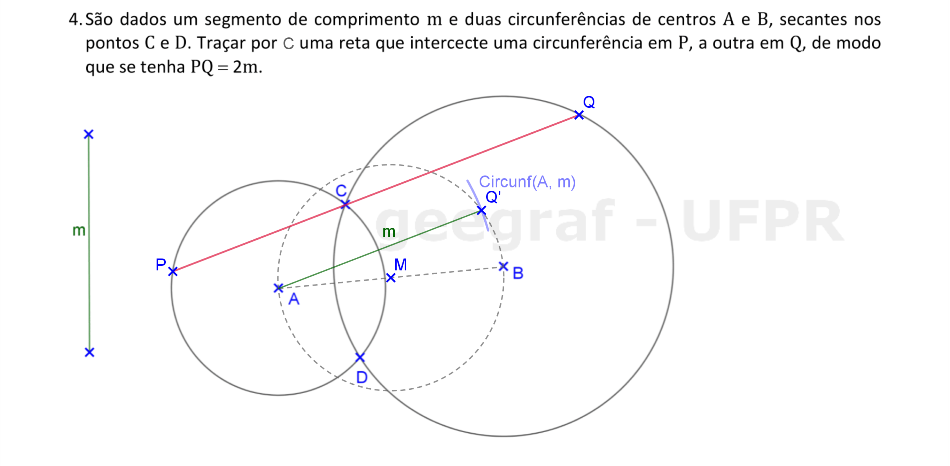
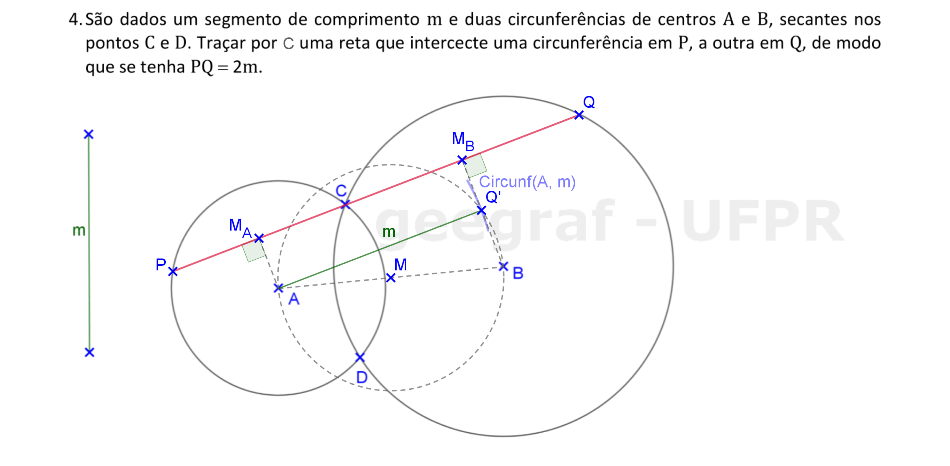
Vamos usar a translação para determinar os pontos P e Q das circunferências dadas, tal que o segmento PQ passa por C e PQ = 2m.
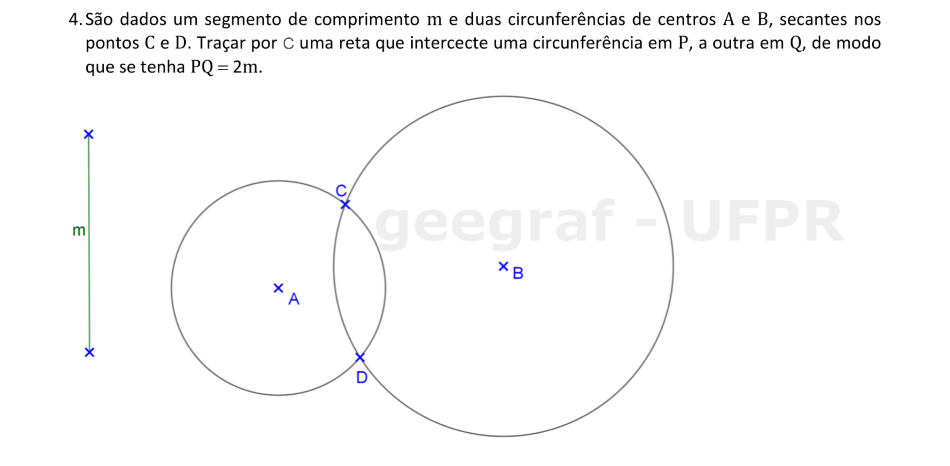

📏 📐 Resolução
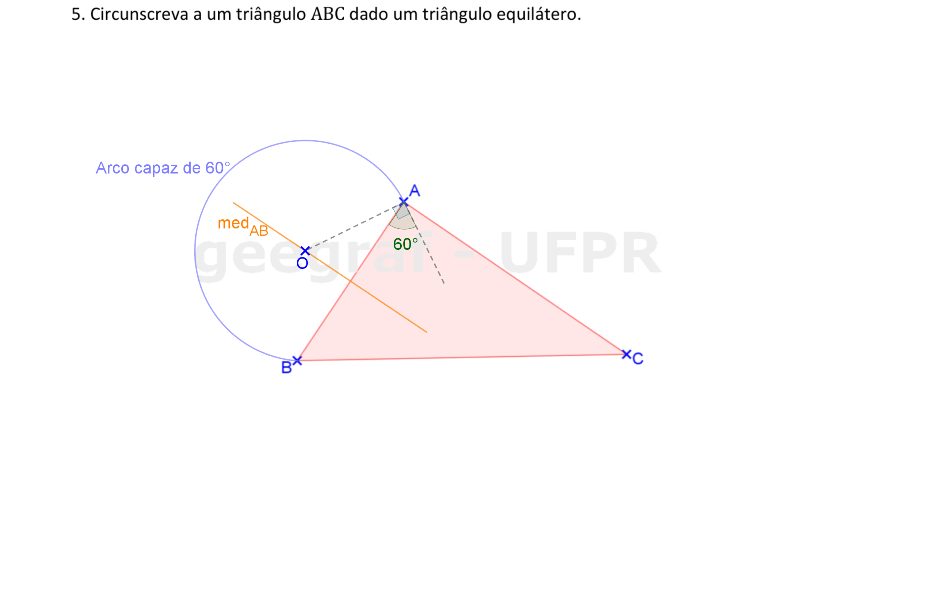
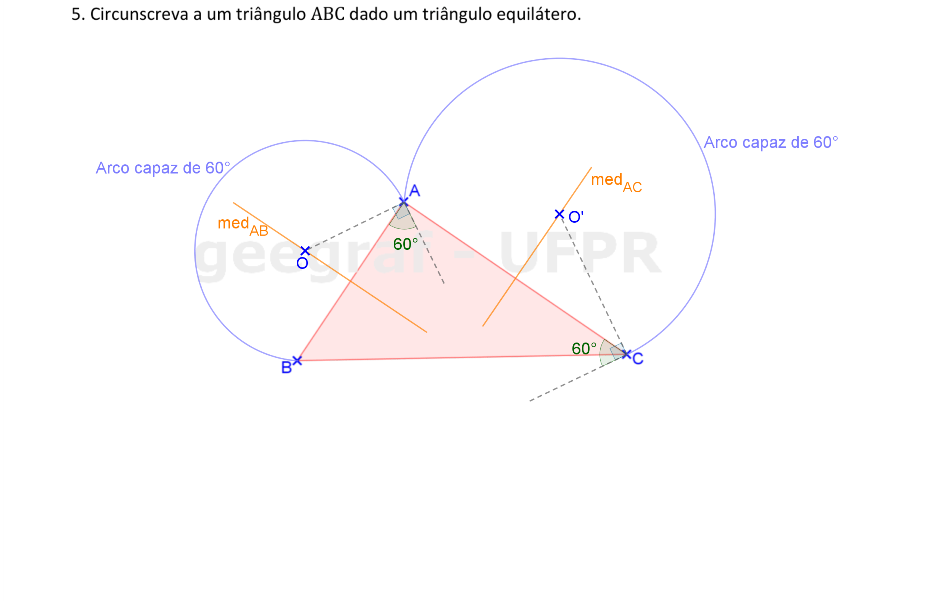
Vamos usar a translação para circunscrever um triângulo equilátero no triângulo △ABC.

📏 📐 Resolução
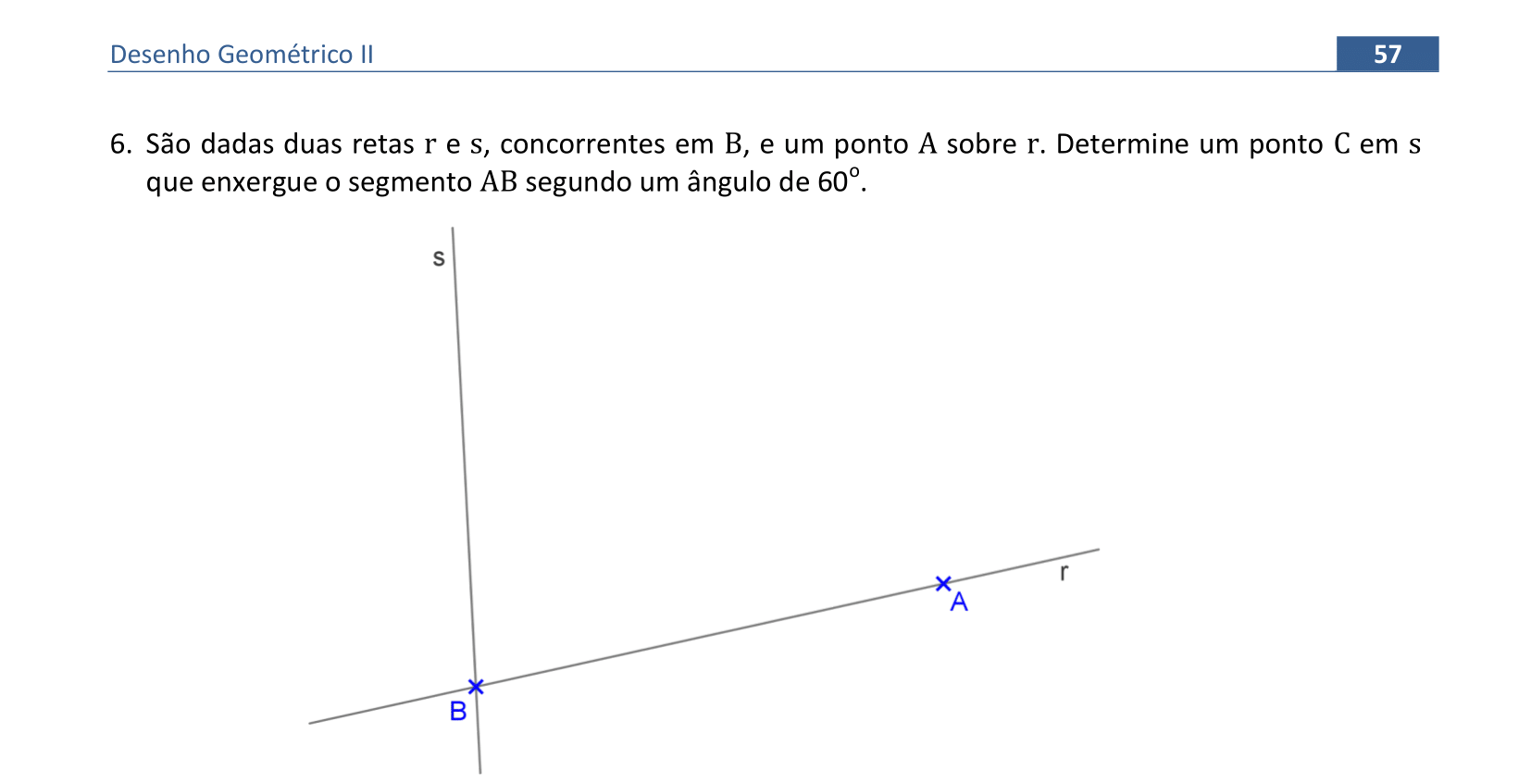
Vamos usar a translação para encontrar um ponto da reta s que enxerga o segmento AB segundo ângulo de 60°.
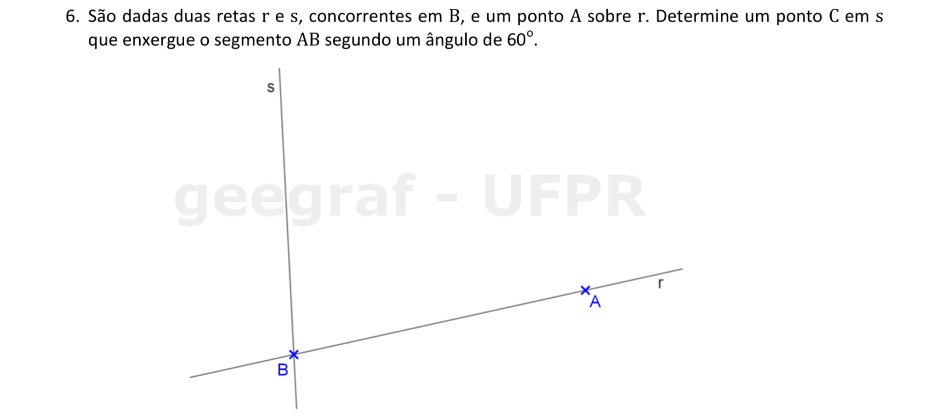



📏 📐 Resolução
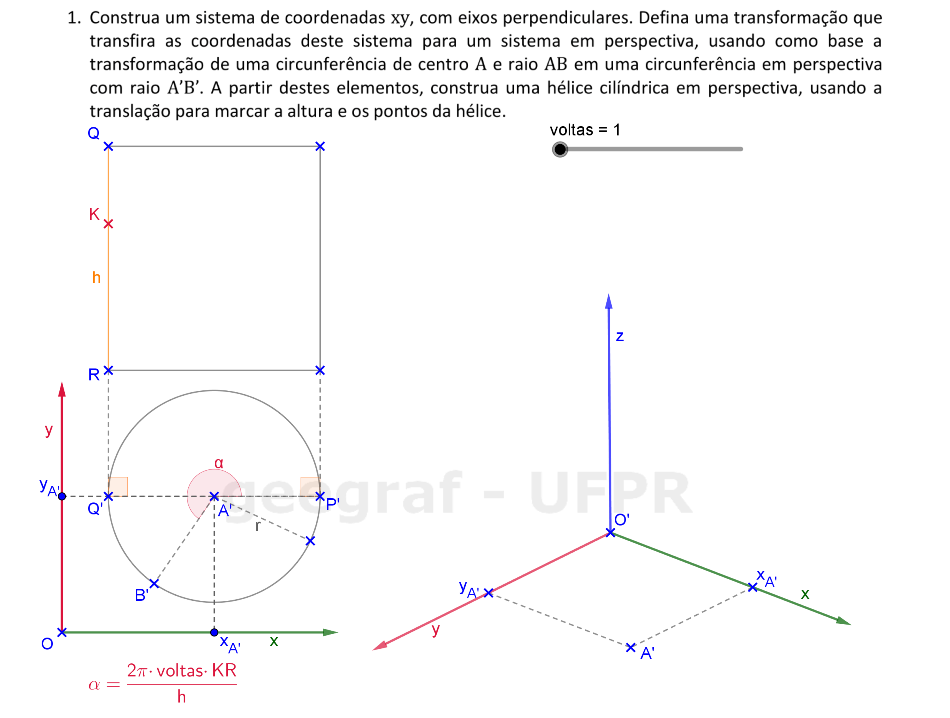
Vamos construir uma hélice cilíndrica em projeções ortogonais e também em perspectiva.


📏 📐 Resolução
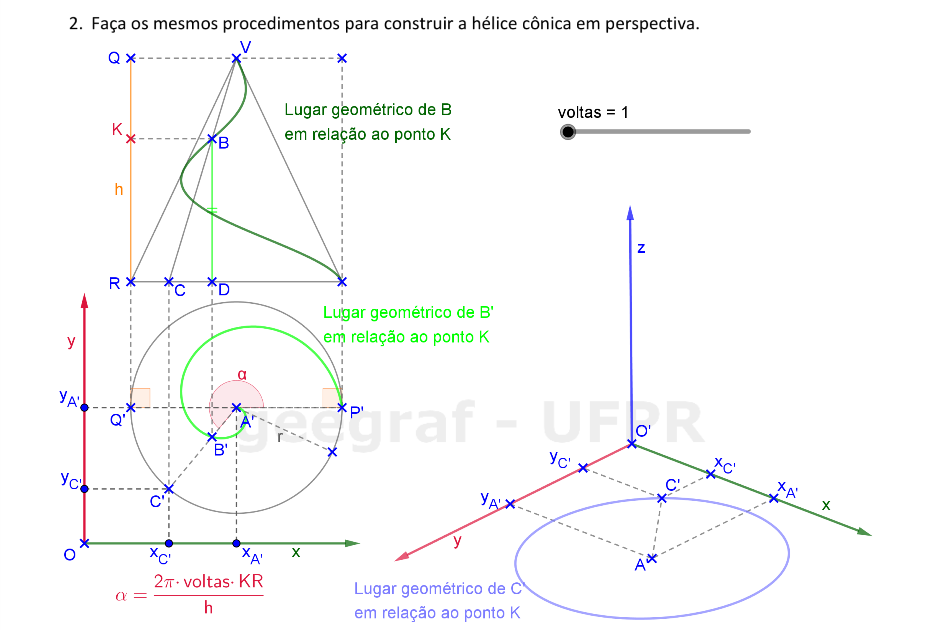
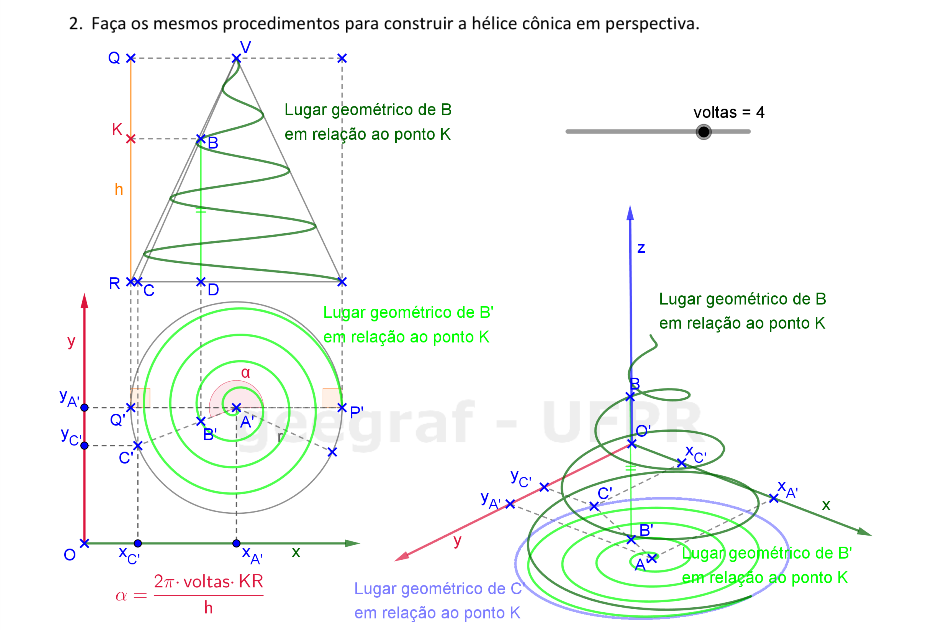
Vamos construir uma hélice cônica em projeções ortogonais e também em perspectiva.


📏 📐 Resolução
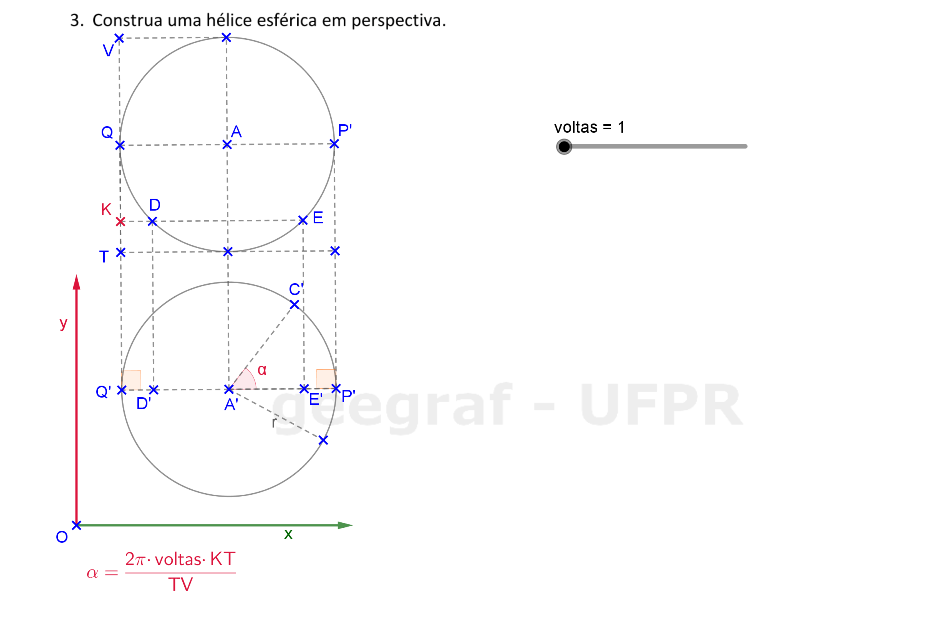
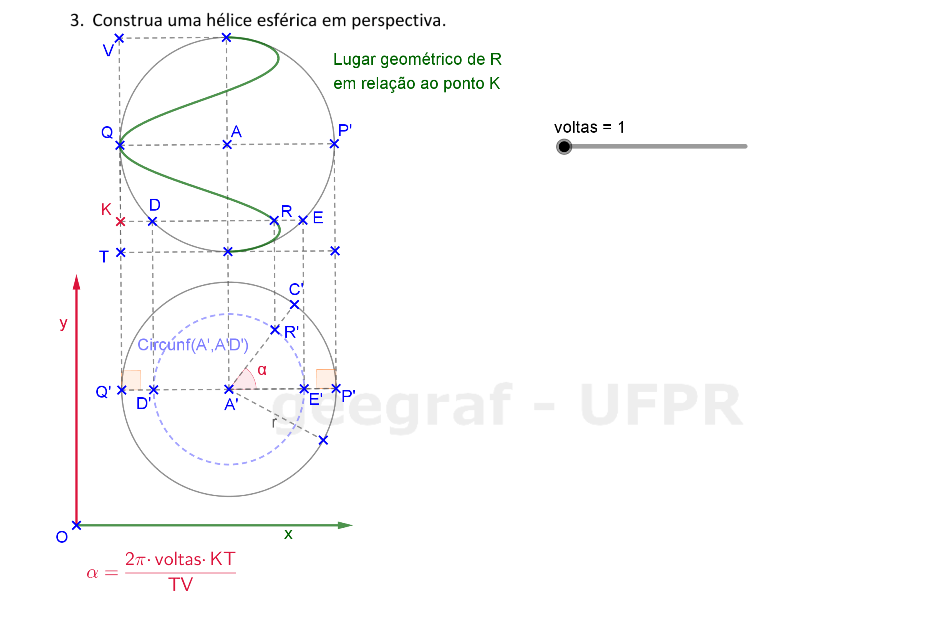
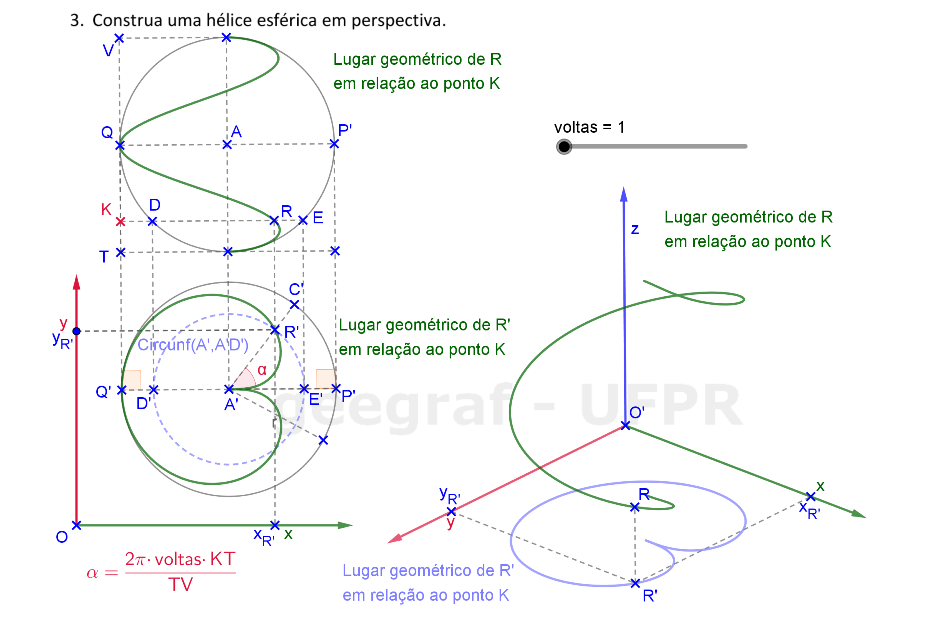
Vamos construir uma hélice esférica em projeções ortogonais e também em perspectiva.



📏 📐 Resolução
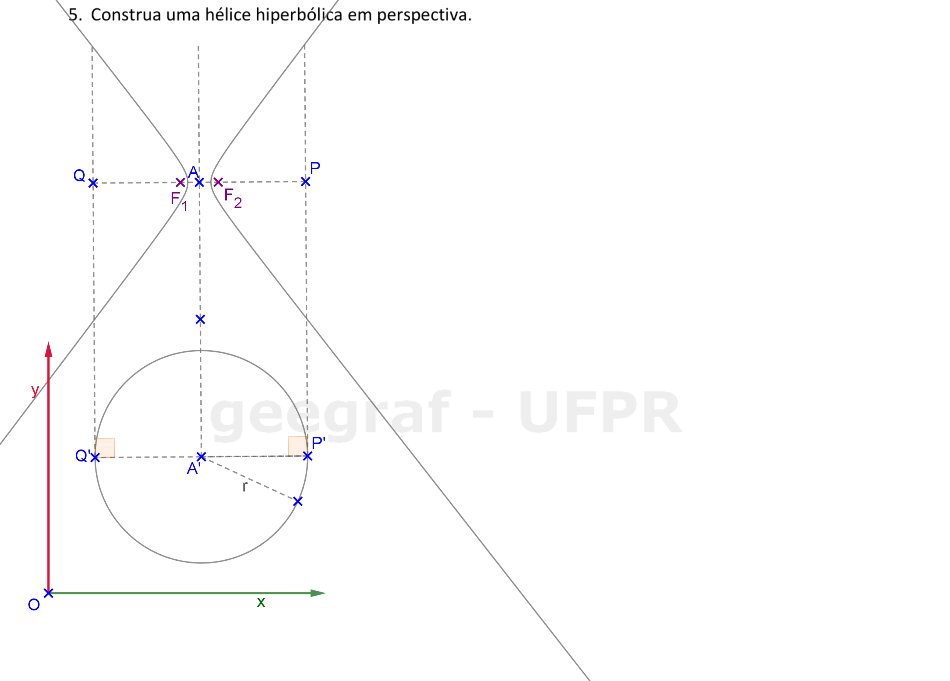
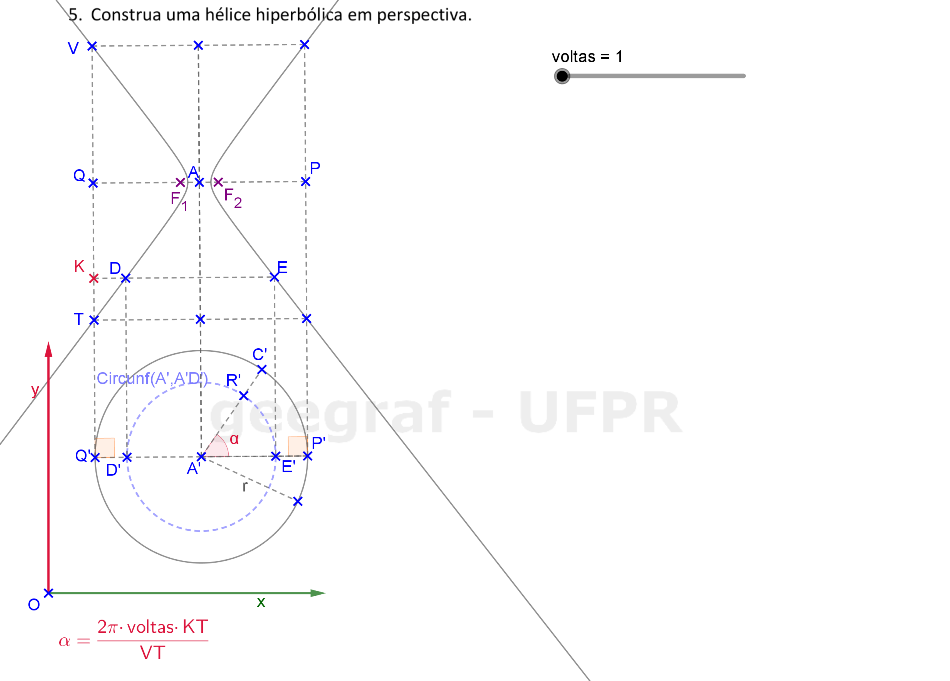
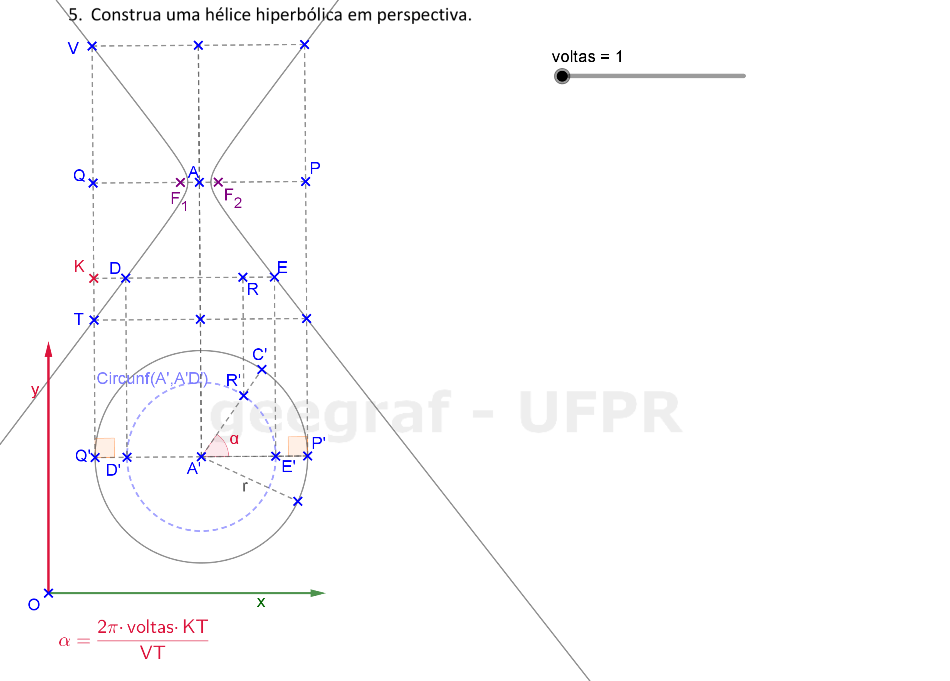
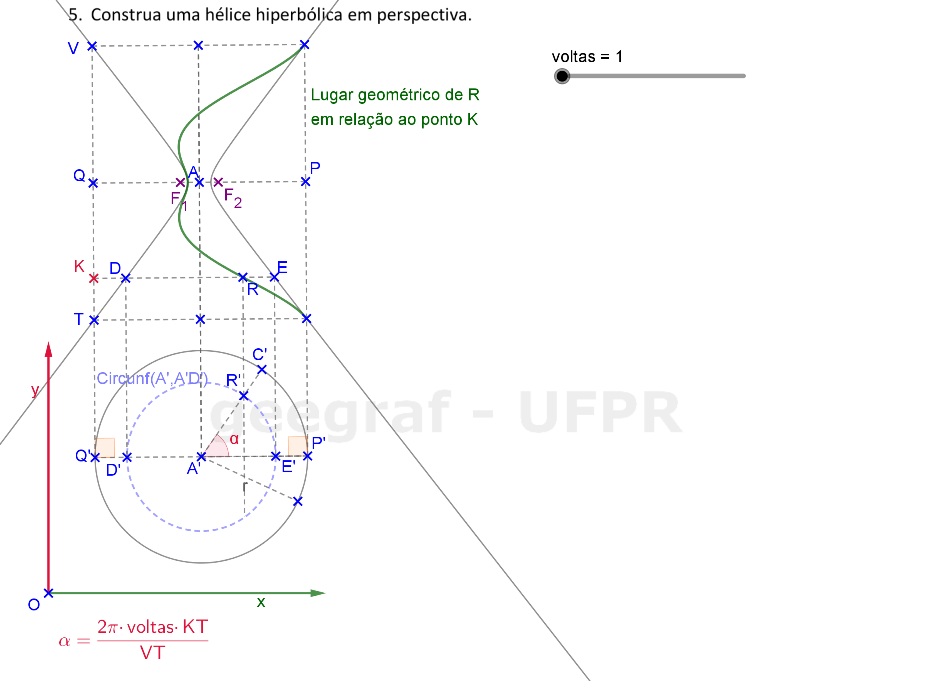
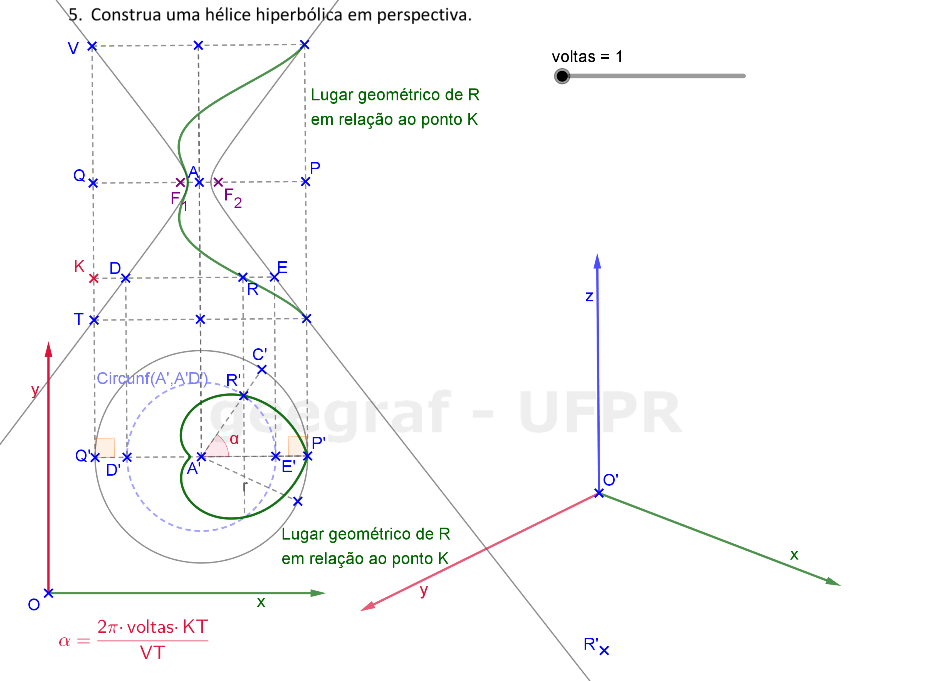
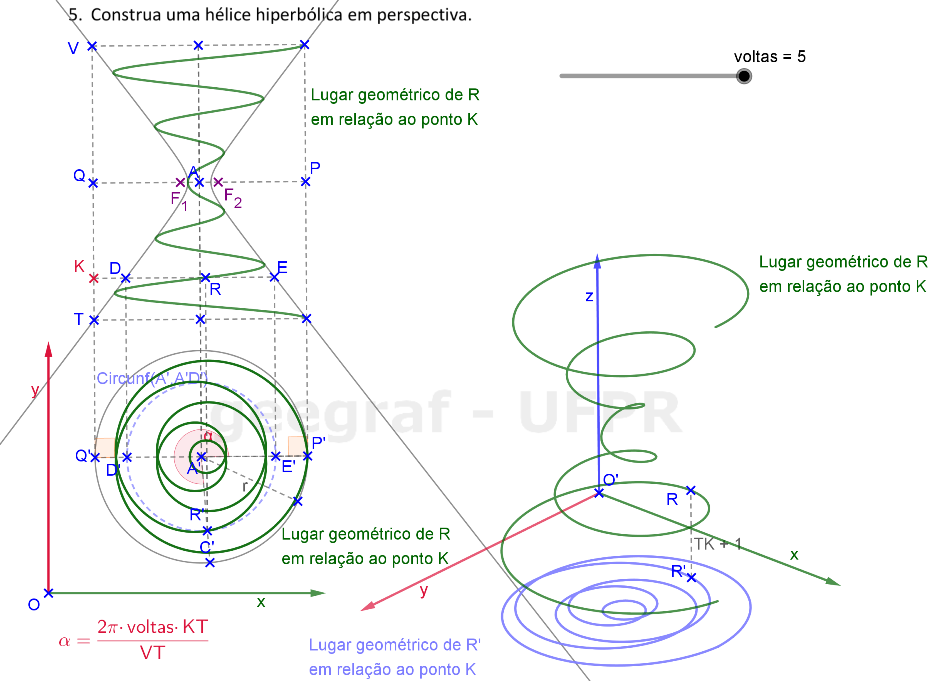
Vamos construir uma hélice hiperbólica em projeções ortogonais e também em perspectiva. Vamos considerar a superfície de um hiperbolóide de revolução.

📏 📐 Resolução
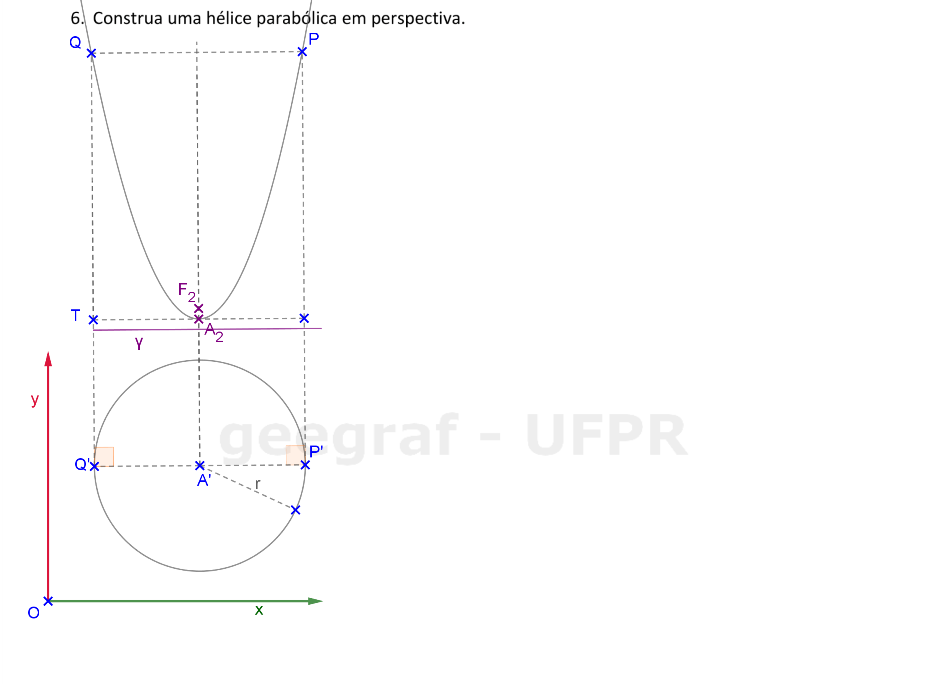
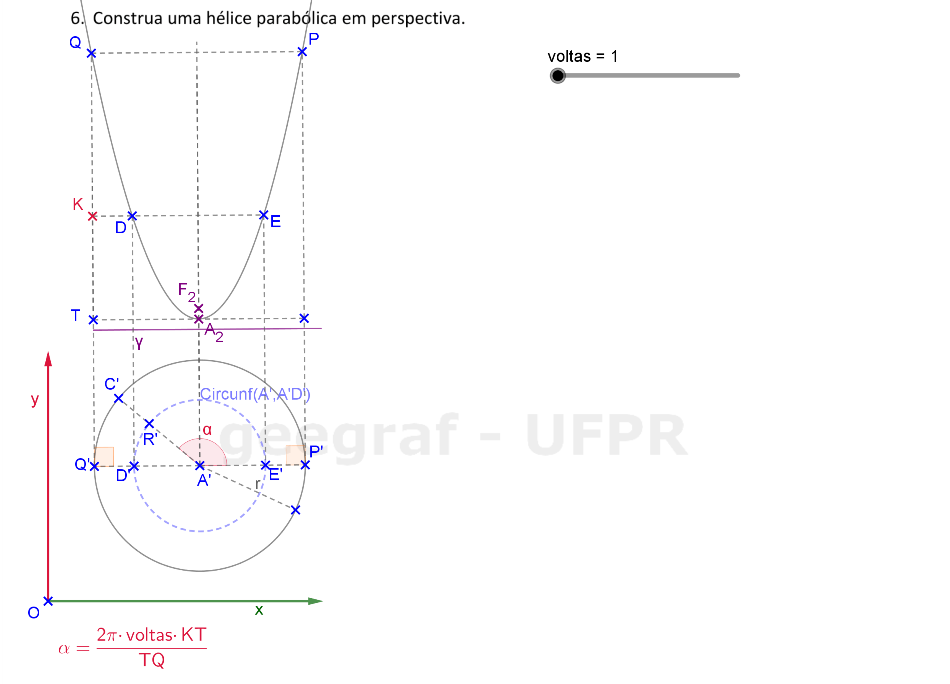
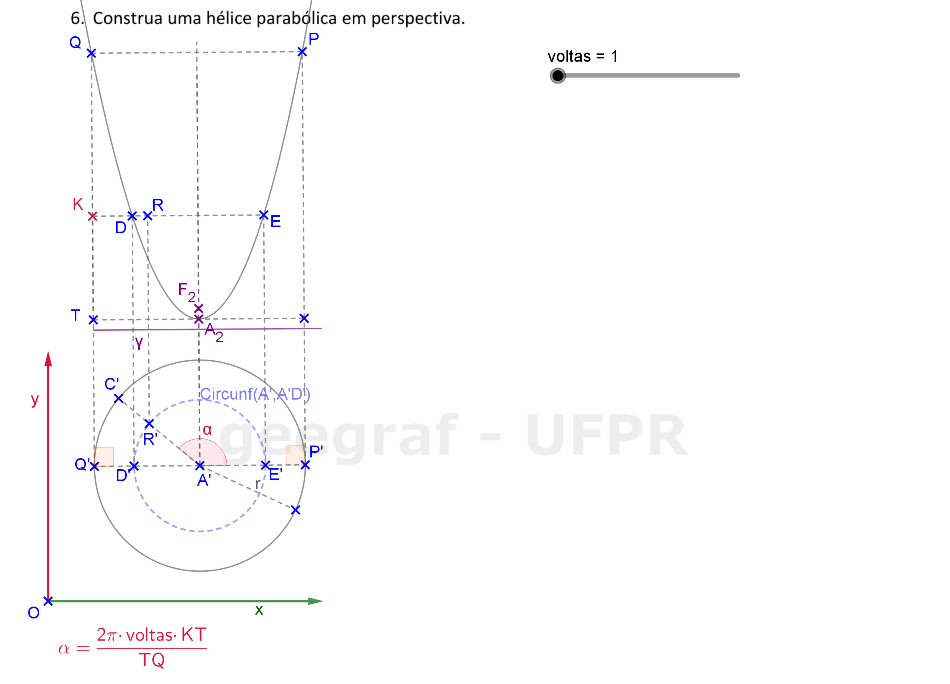
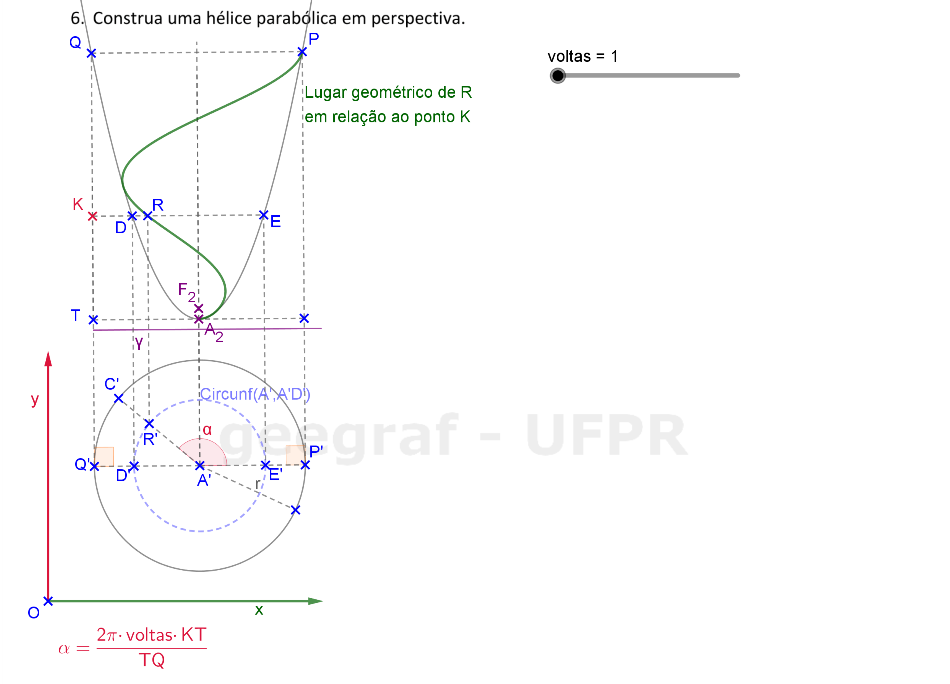
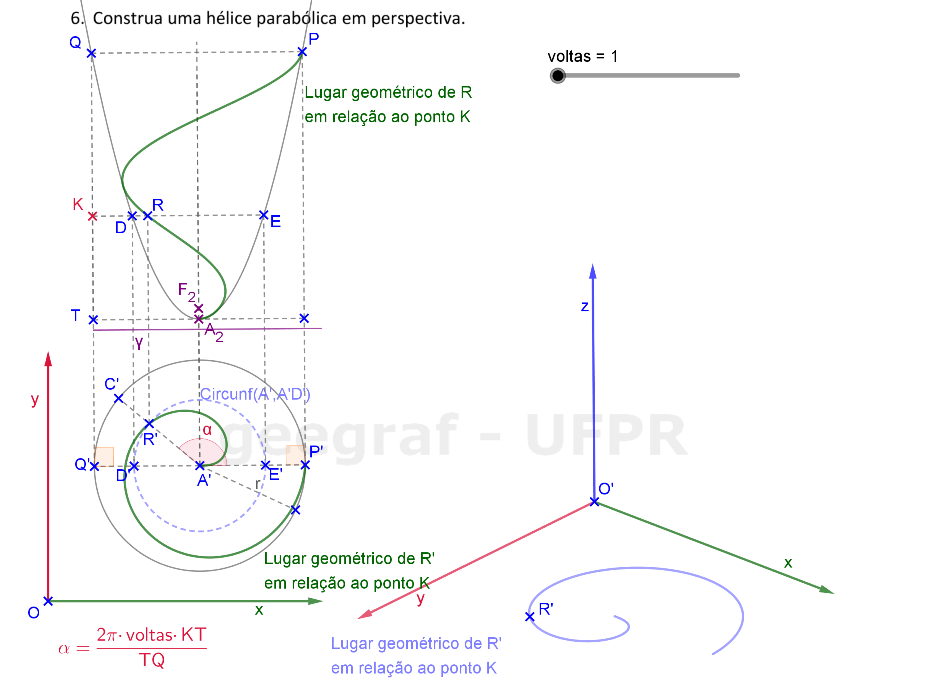
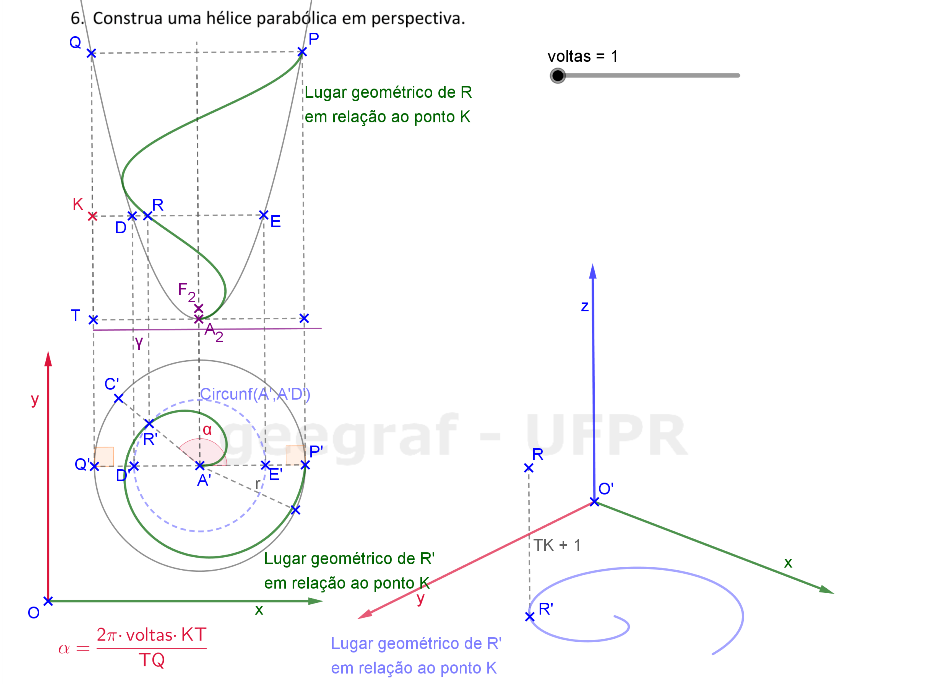
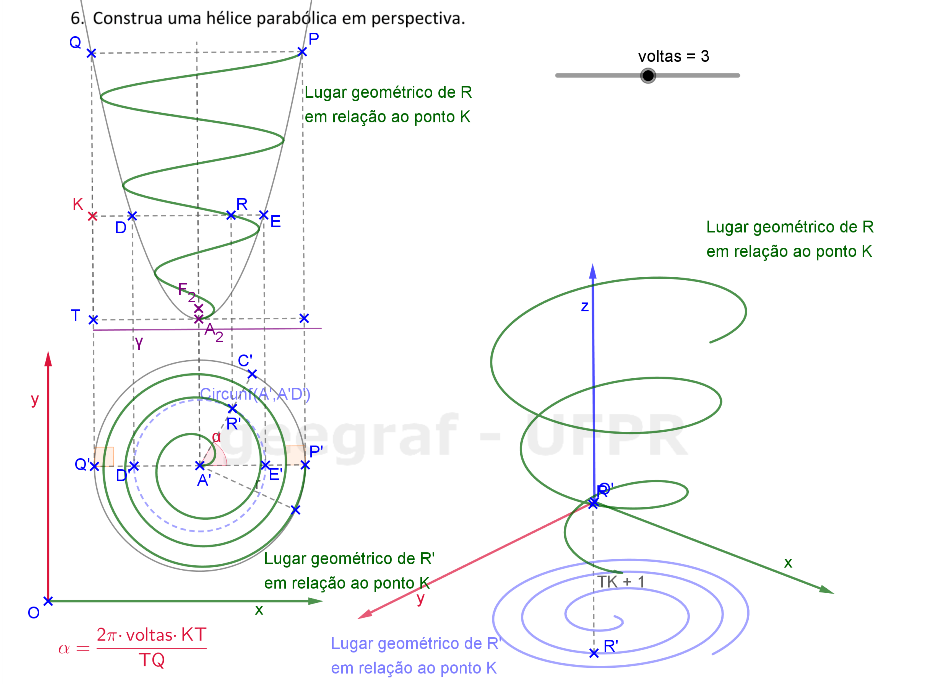
Vamos construir uma hélice parabólica em projeções ortogonais e também em perspectiva. Vamos considerar a superfície de um parabolóide de revolução.


📏 📐 Resolução
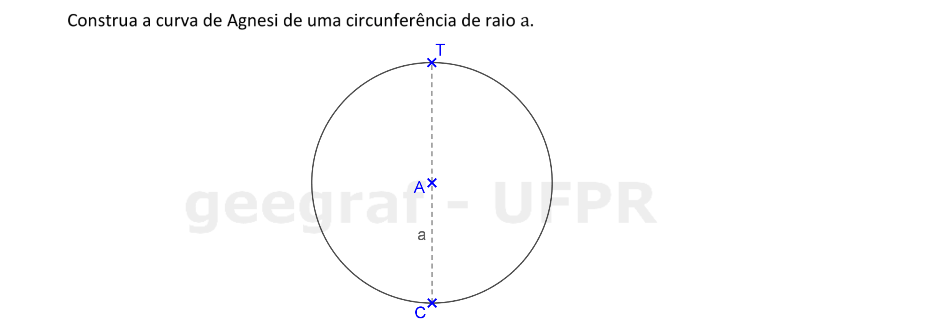
Vamos construir uma curva de Agnesi a partir de uma circunferência de centro A e raio a.

📏 📐 Resolução
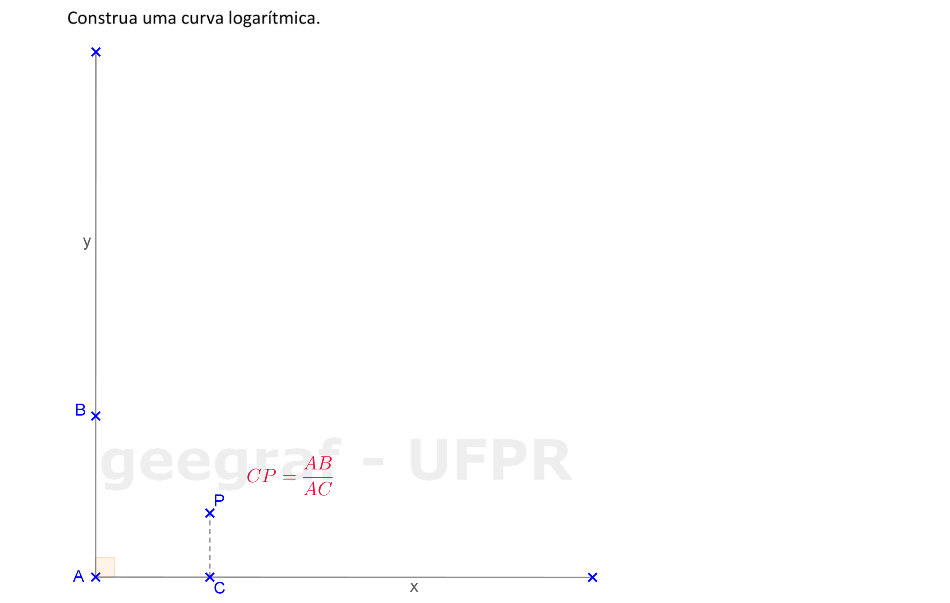
Vamos construir uma curva logarítmica a partir dos eixos x e y.


📏 📐 Resolução
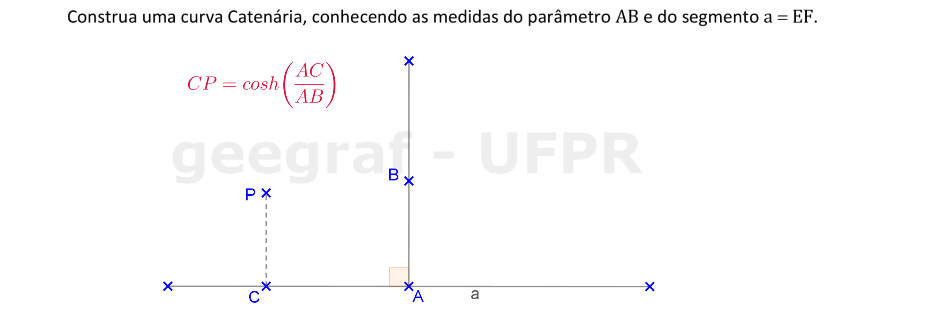
Vamos construir uma curva Catenária a partir de dois segmentos perpendiculares.

📏 📐 Resolução
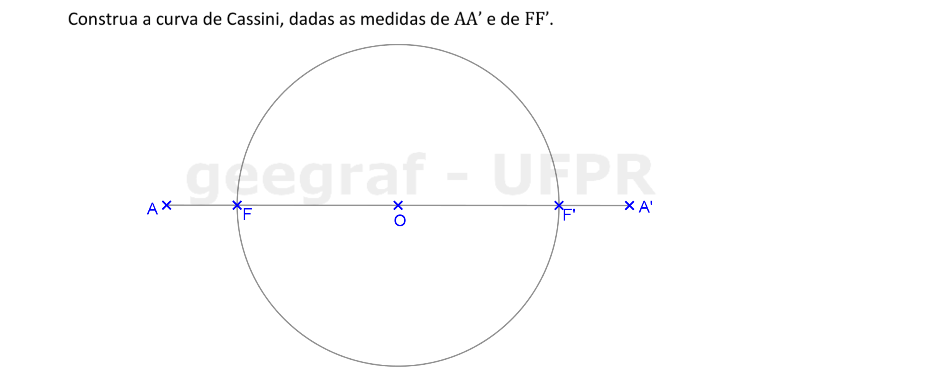
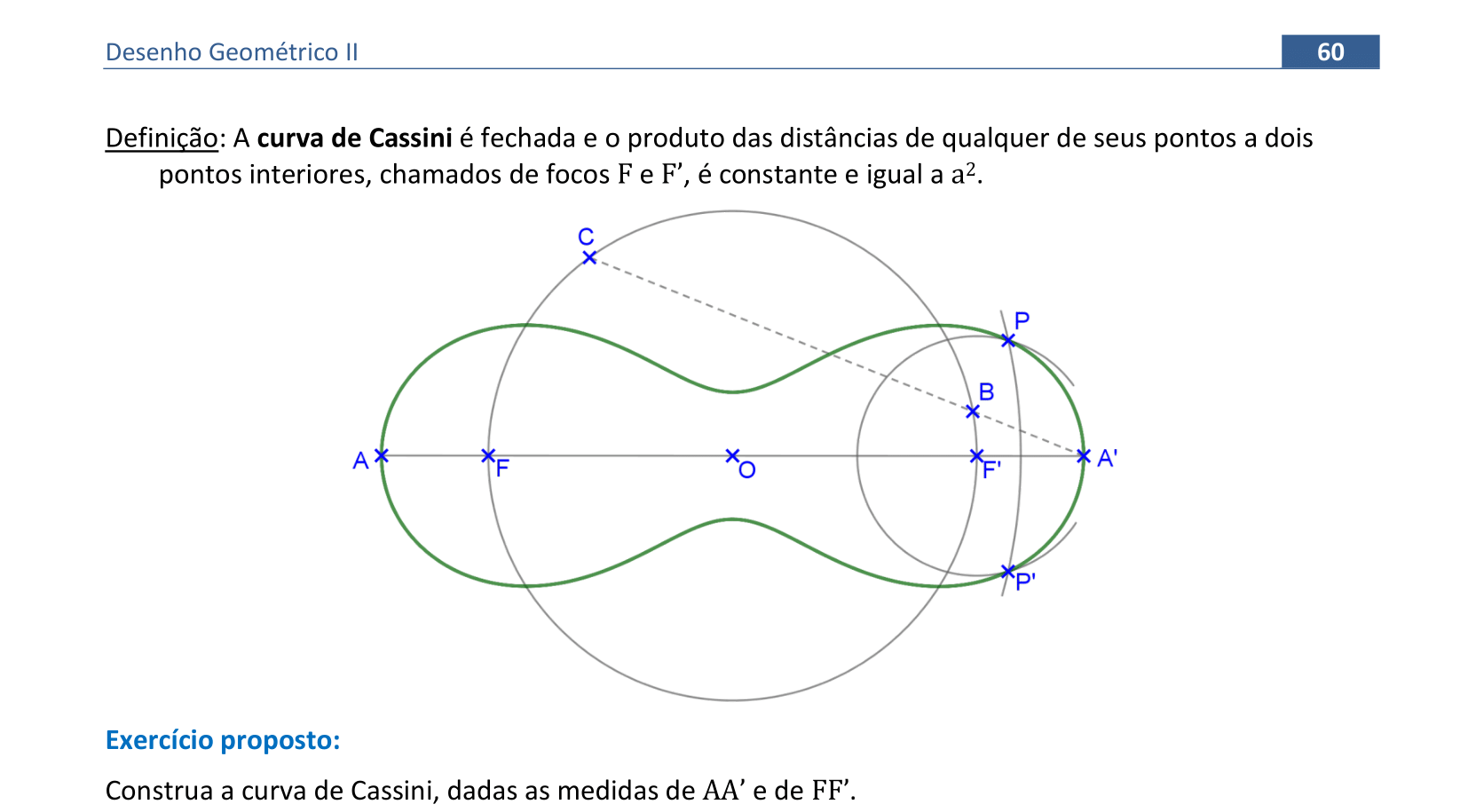
Vamos construir uma curva de Cassini a partir dos segmentos AA' e FF'.

📏 📐 Resolução
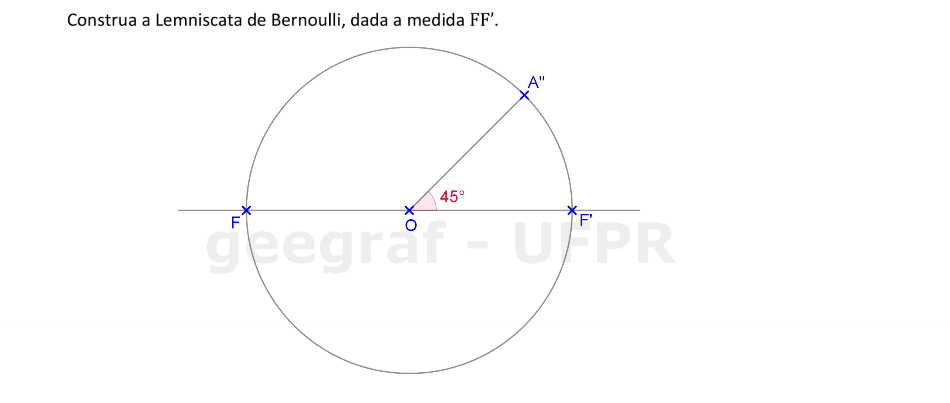
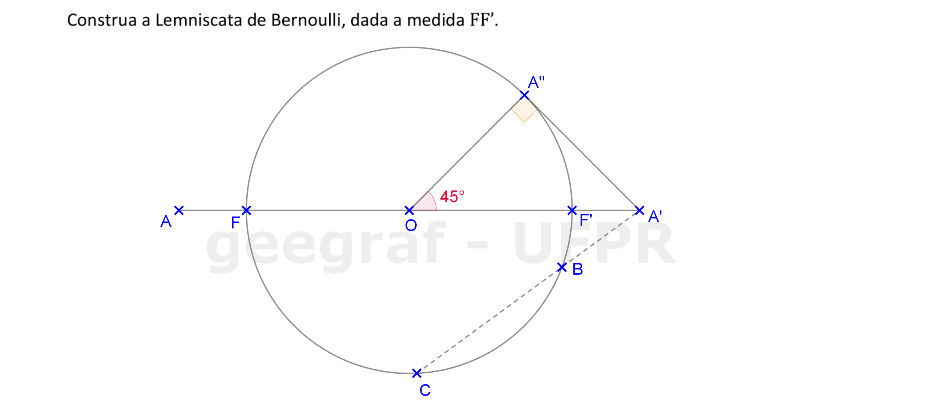
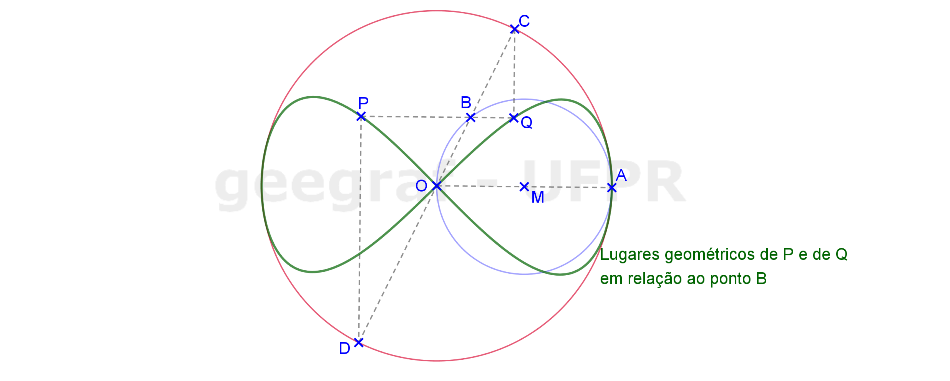
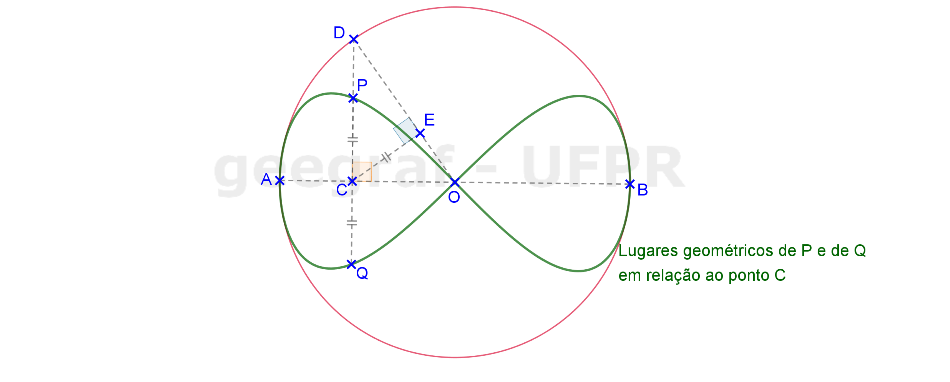
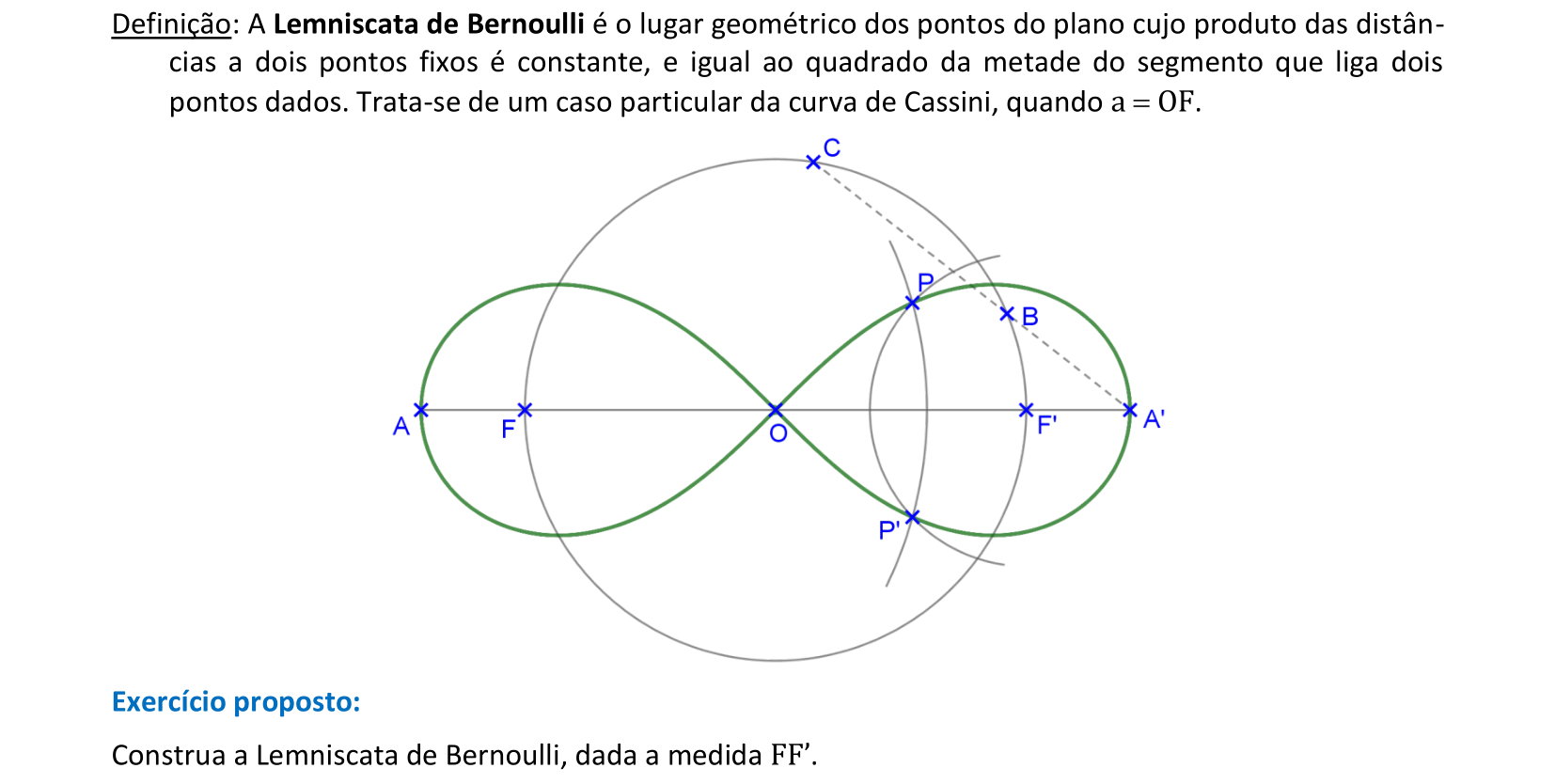
Vamos construir uma curva lemniscata de Bernoulli a partir do segmento FF'.

📏 📐 Resolução
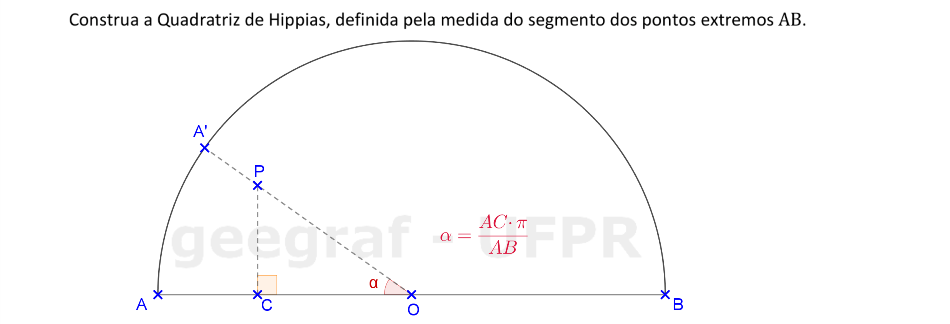
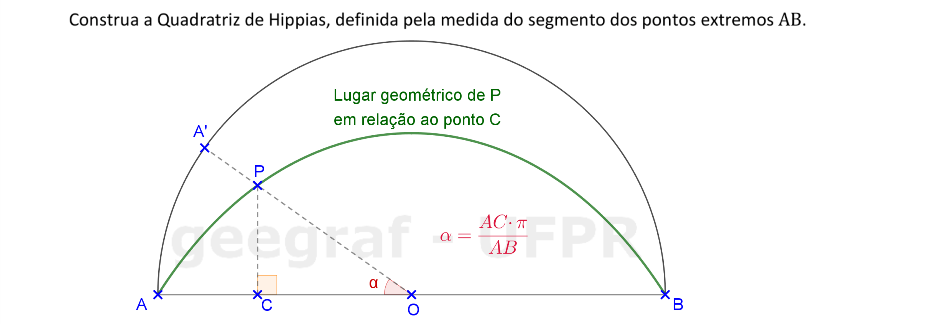
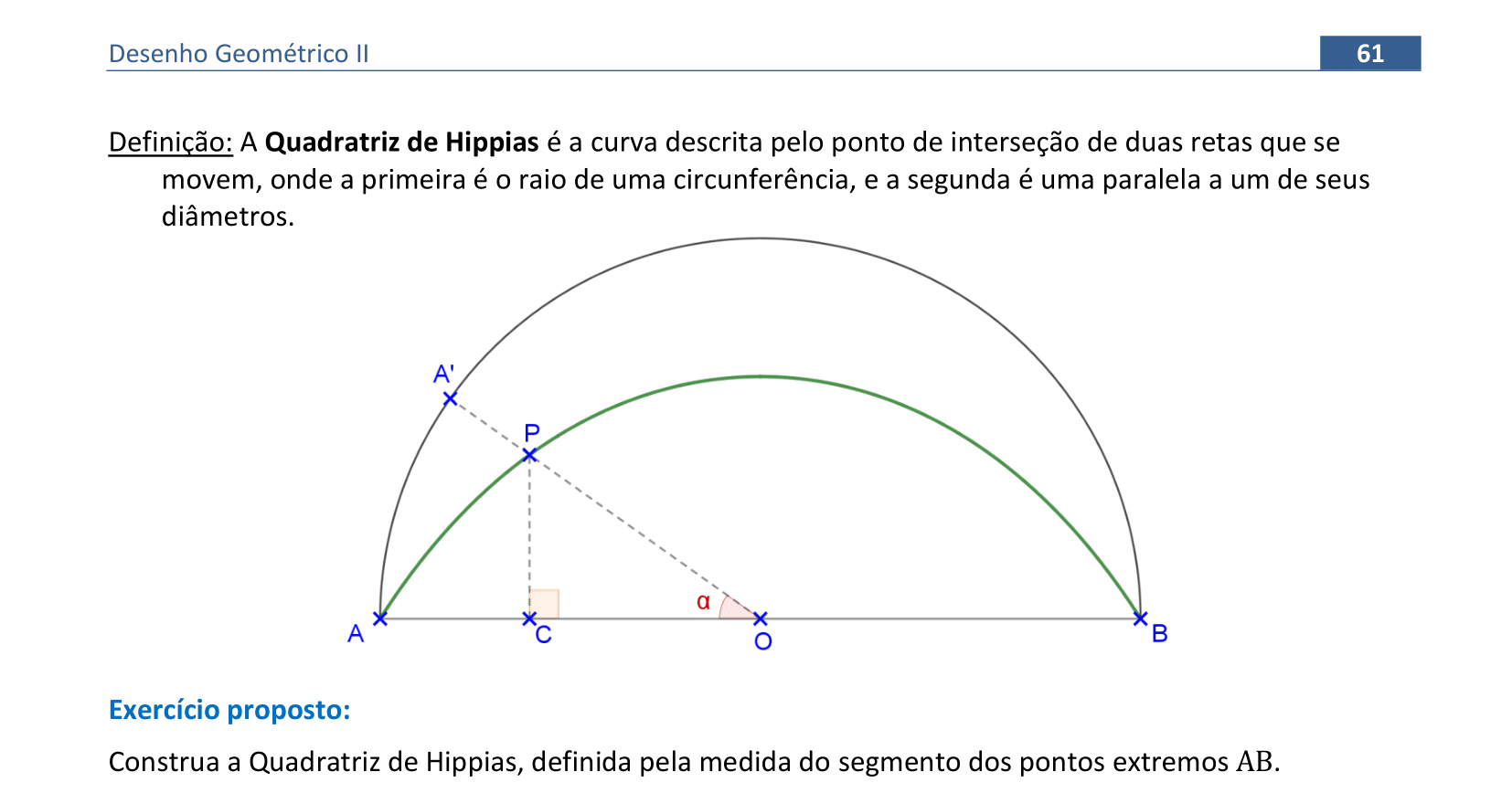
Vamos construir uma quadratriz de Hippias a partir do segmento AB.

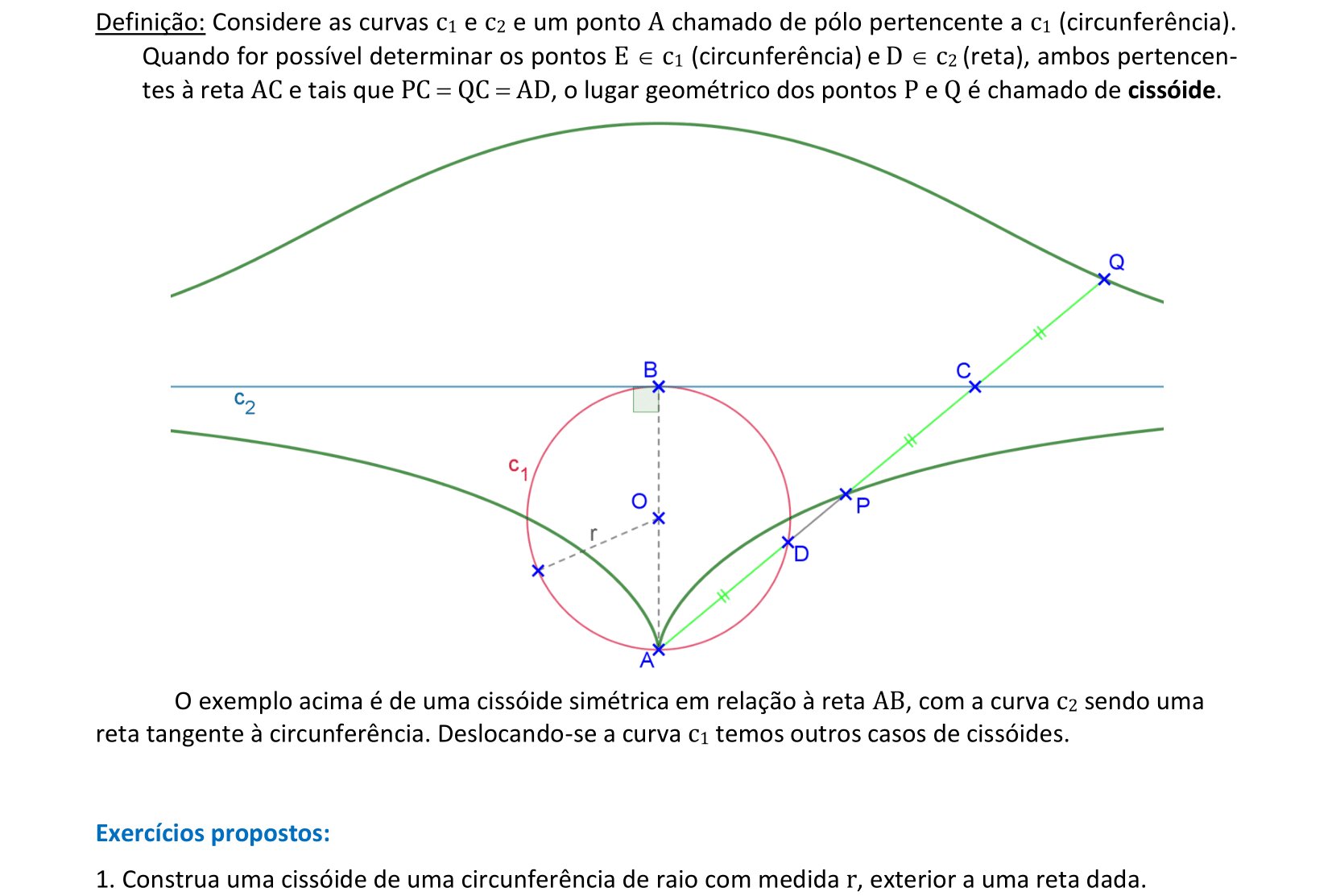
📏 📐 Resolução
Vamos construir uma cissóide de uma circunferência exterior a uma reta.


📏 📐 Resolução
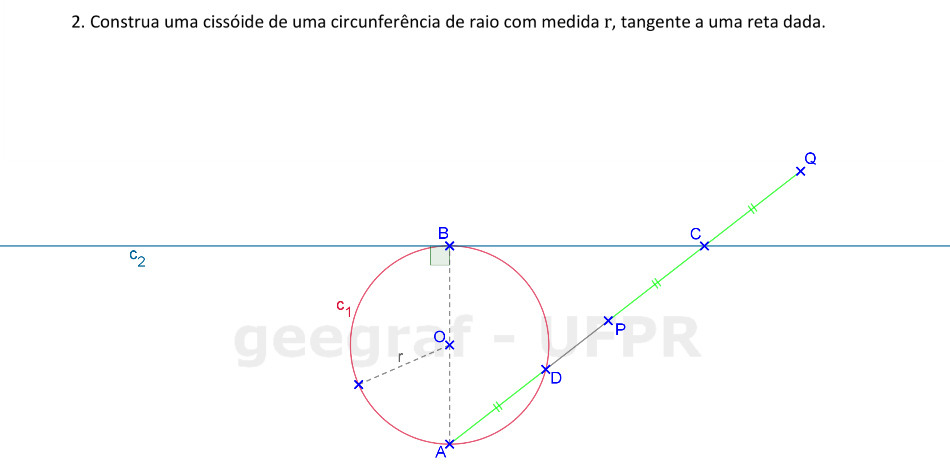
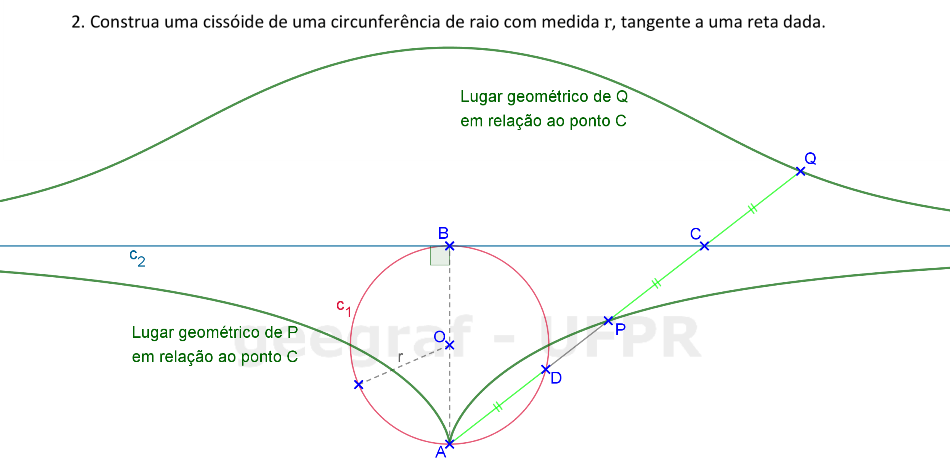
Vamos construir uma cissóide de uma circunferência tangente a uma reta.



📏 📐 Resolução
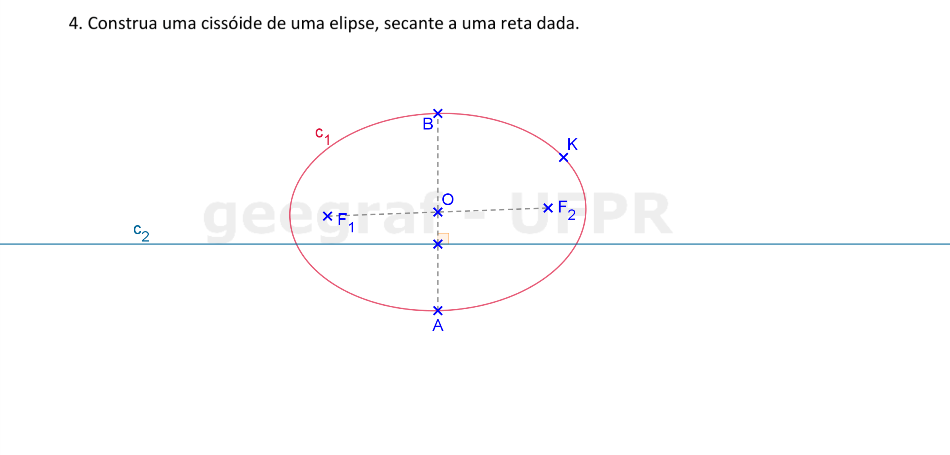
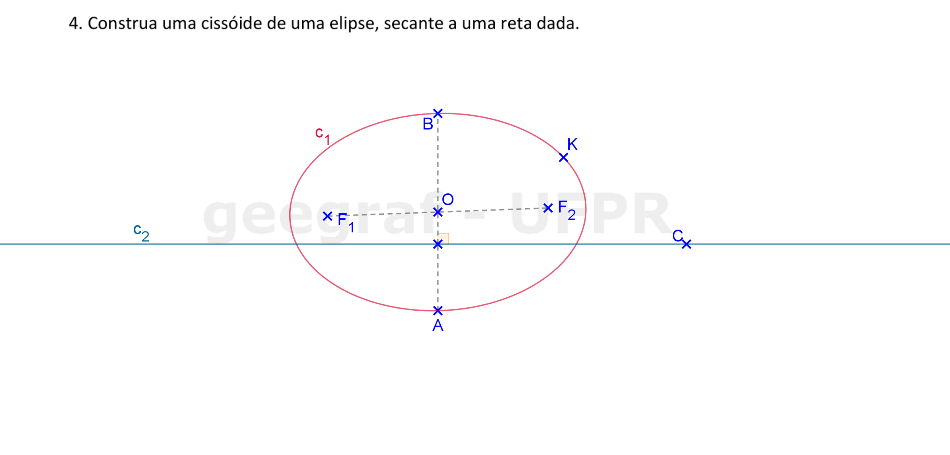
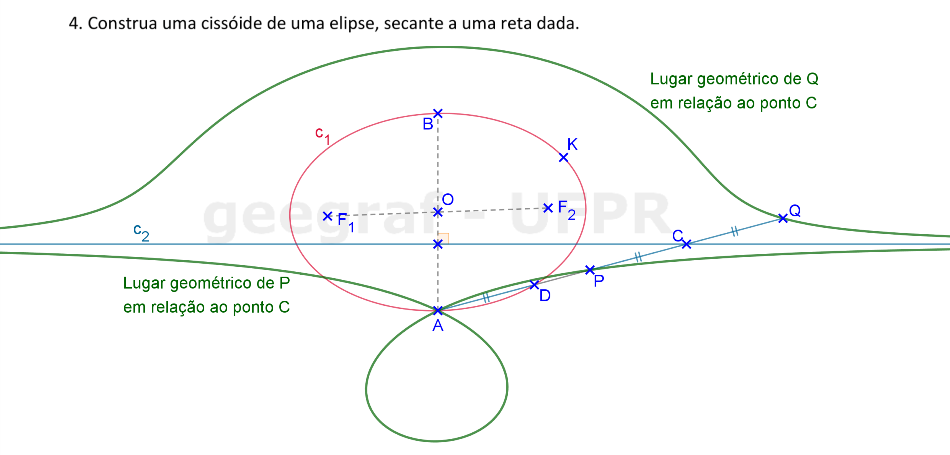
Vamos construir uma cissóide de uma elipse secante a uma reta.


📏 📐 Resolução
Vamos construir uma cissóide de uma hipérbole secante a uma reta.


📏 📐 Resolução
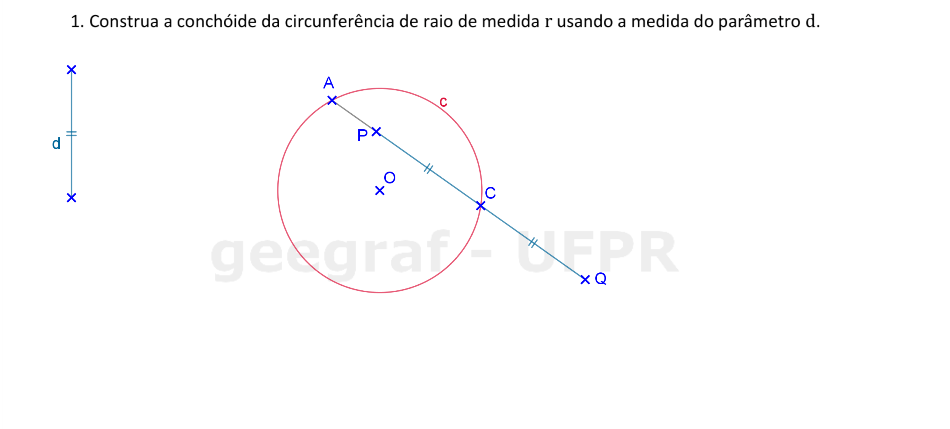
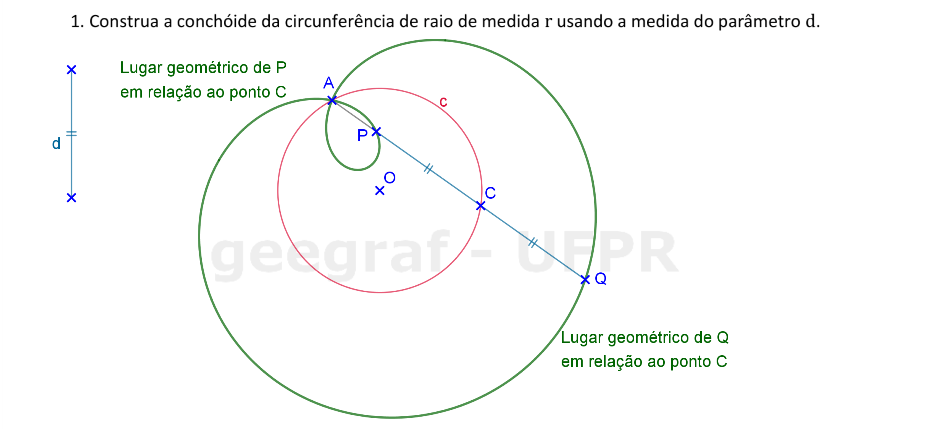
Vamos construir uma conchóide de uma circunferência com parâmetro d e pólo A.


📏 📐 Resolução
Vamos construir uma conchóide de uma circunferência com parâmetro igual ao diâmetro d e pólo A.


📏 📐 Resolução
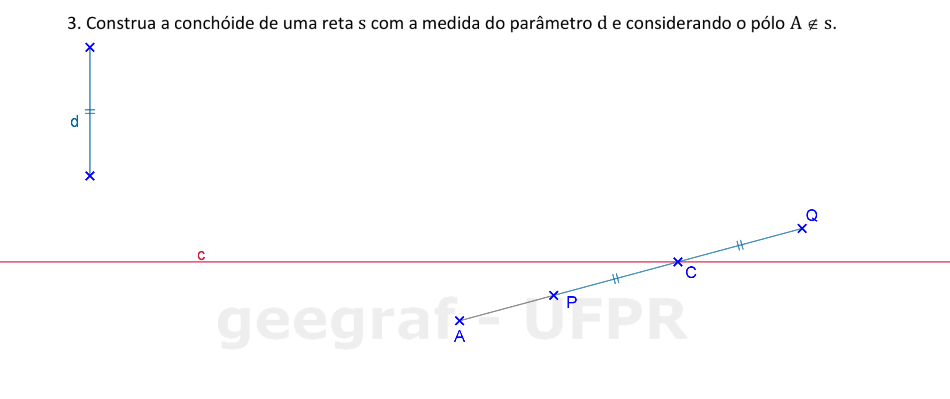
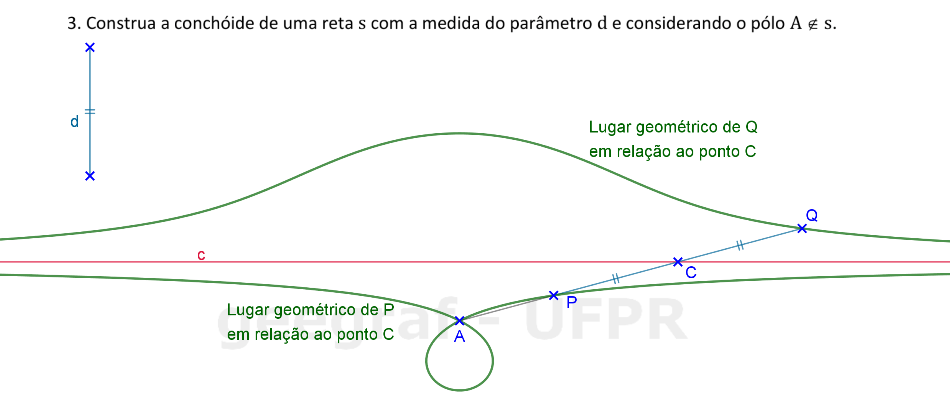
Vamos construir uma conchóide de uma reta com parâmetro d e pólo A.


📏 📐 Resolução
Vamos construir uma conchóide de uma hipérbole com parâmetro d e pólo A.


📏 📐 Resolução
Vamos construir uma besácea com parâmetros AB e AC.


📏 📐 Resolução
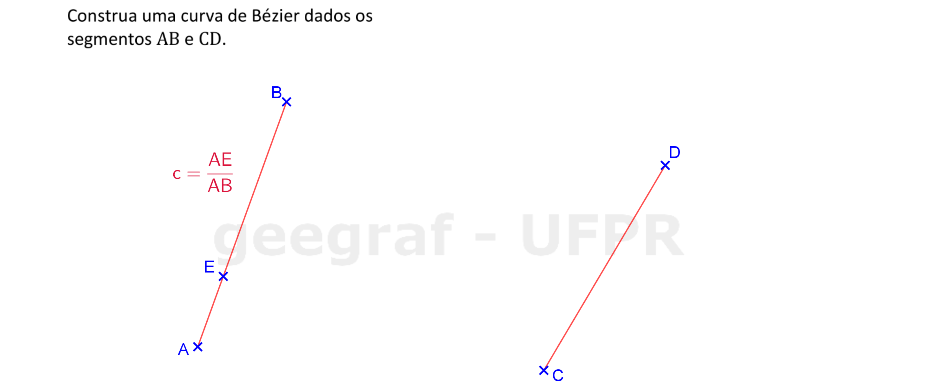
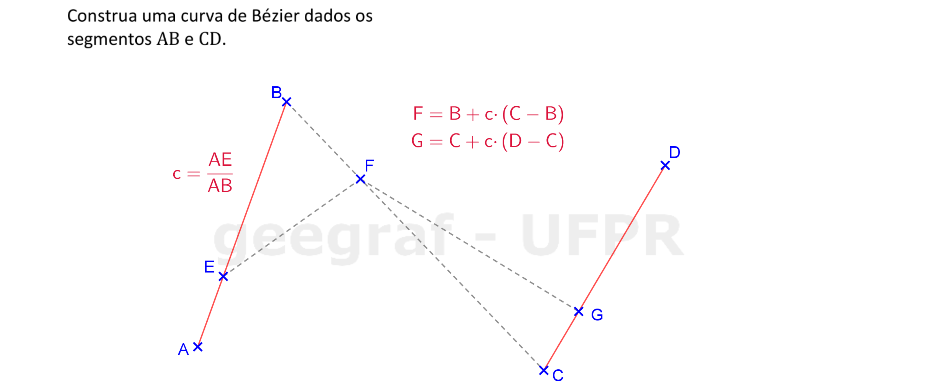
Vamos construir uma curva de Bézier dados os segmentos de controle AB e CD.



📏 📐 Resolução
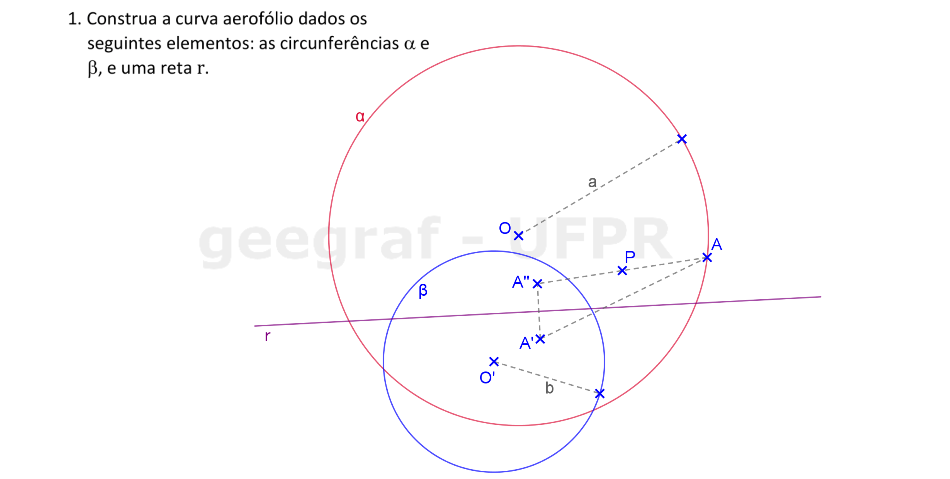
Vamos construir uma curva aerofólio dadas as circunferências α e β e a reta r.

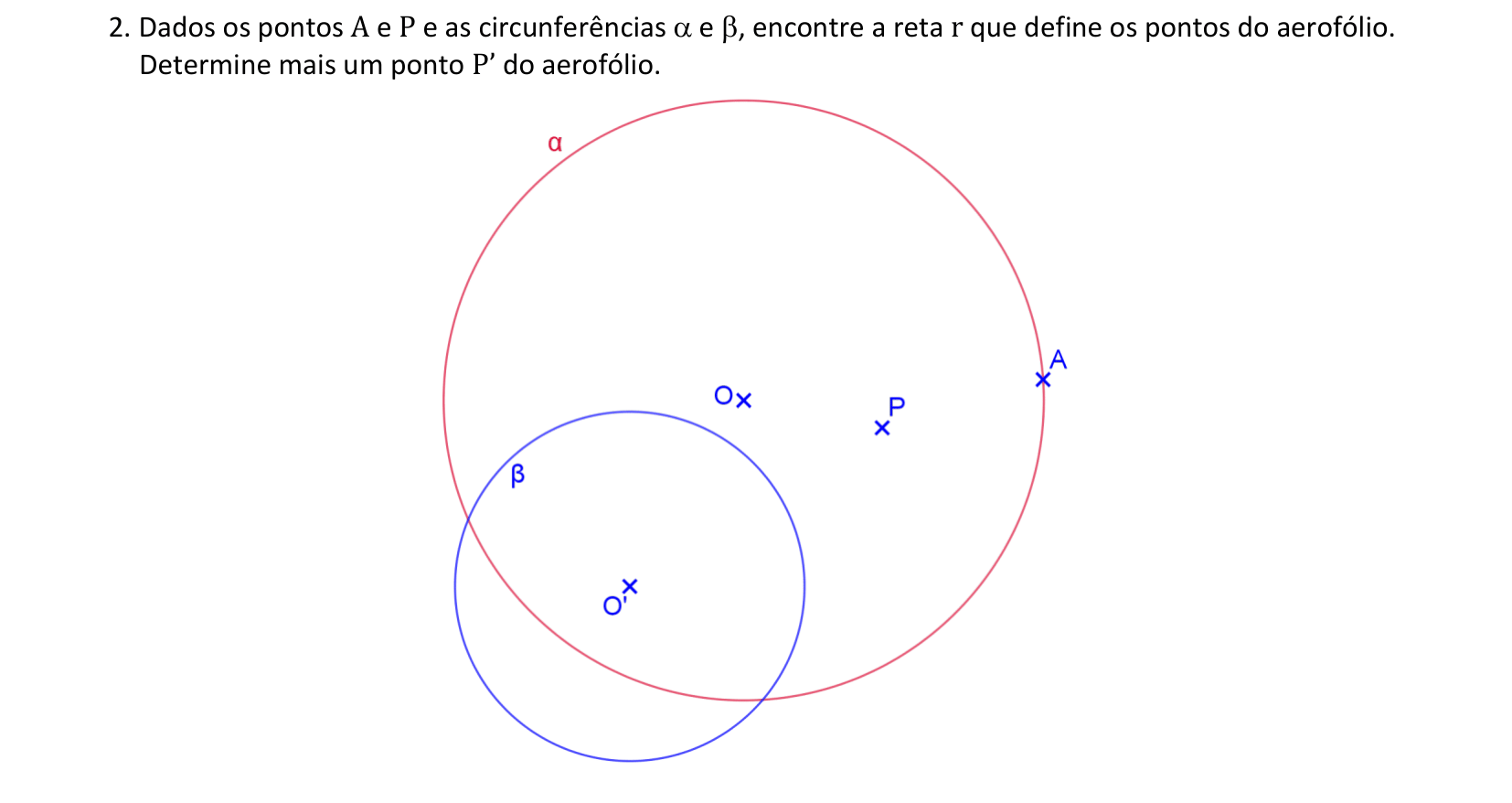
📏 📐 Resolução
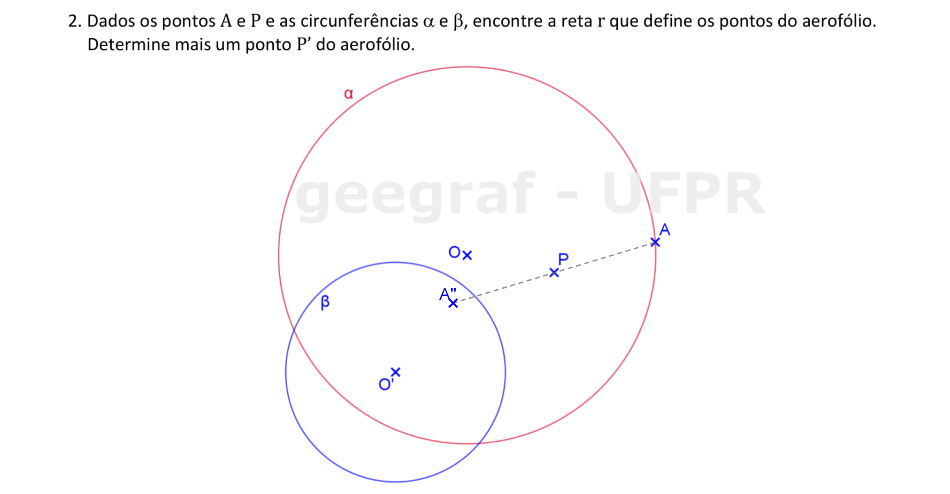
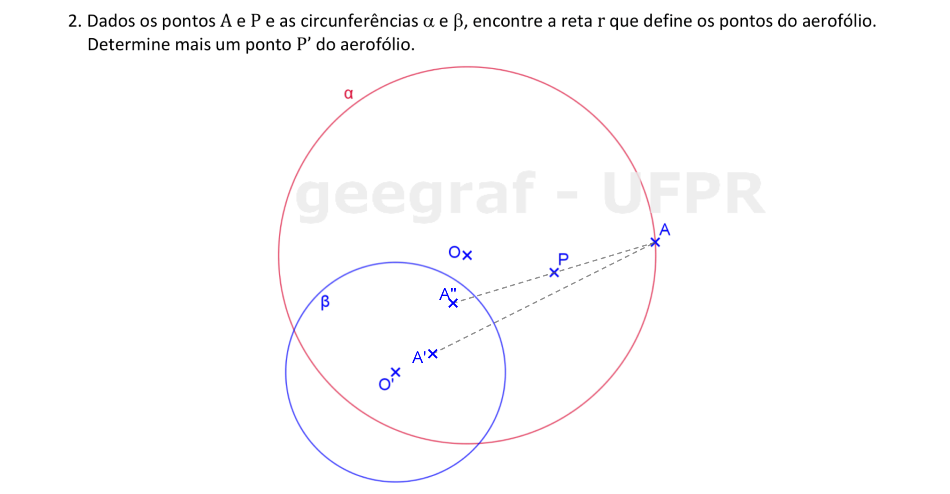
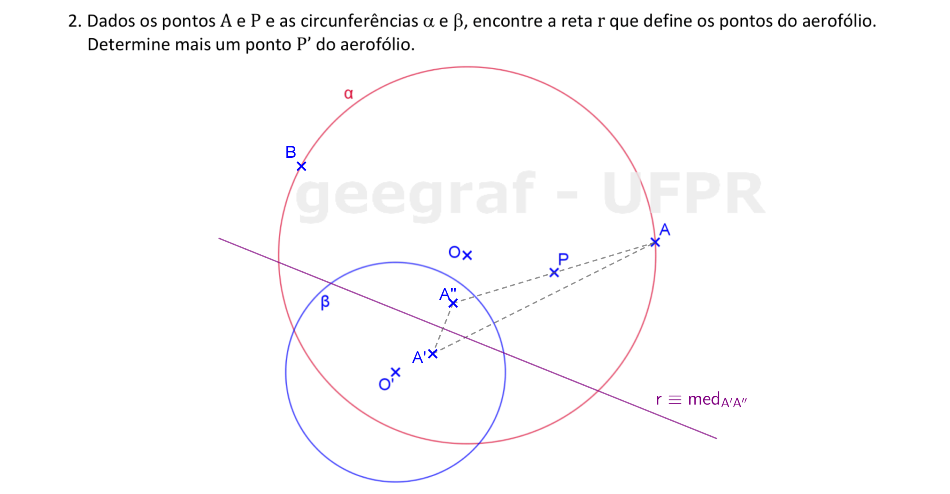
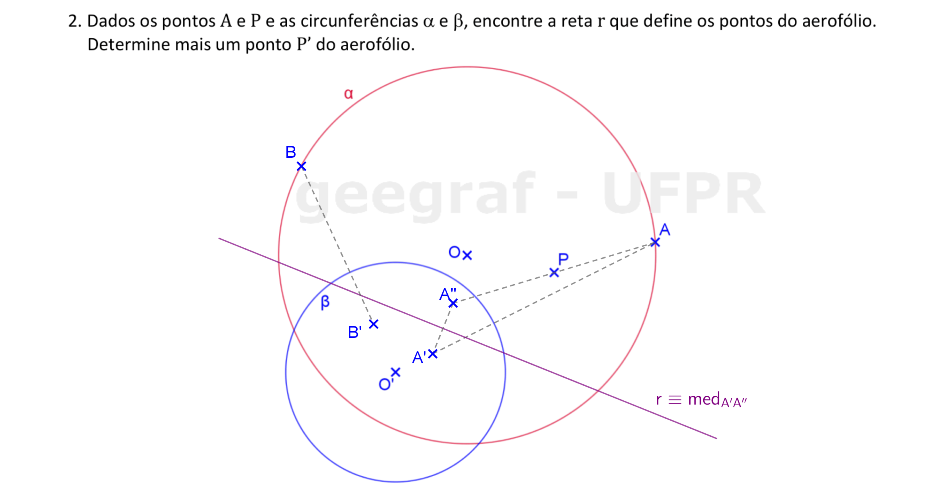
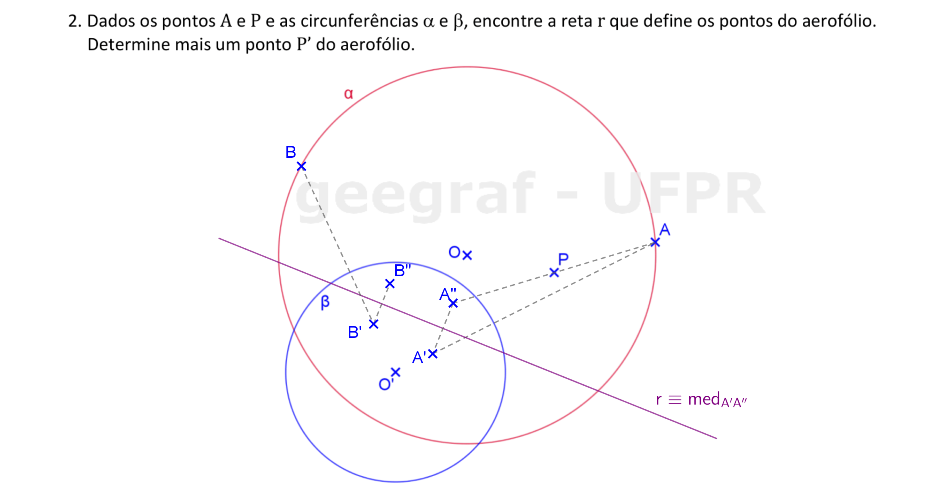
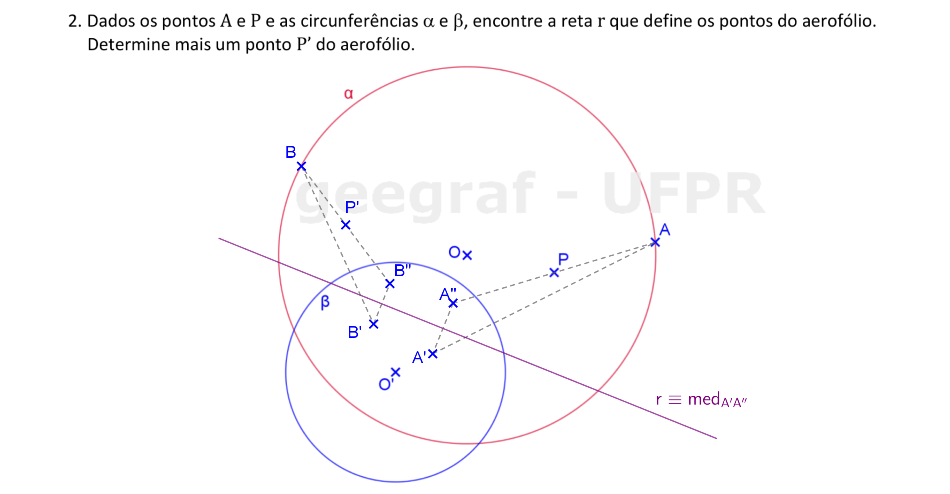
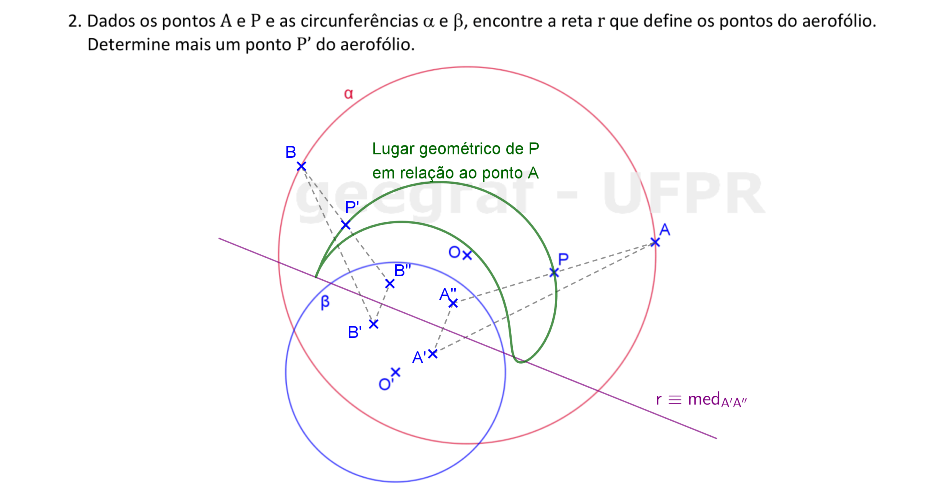
Vamos determinar a reta que define uma curva aerofólio que passa por P, dadas as circunferências α e β.

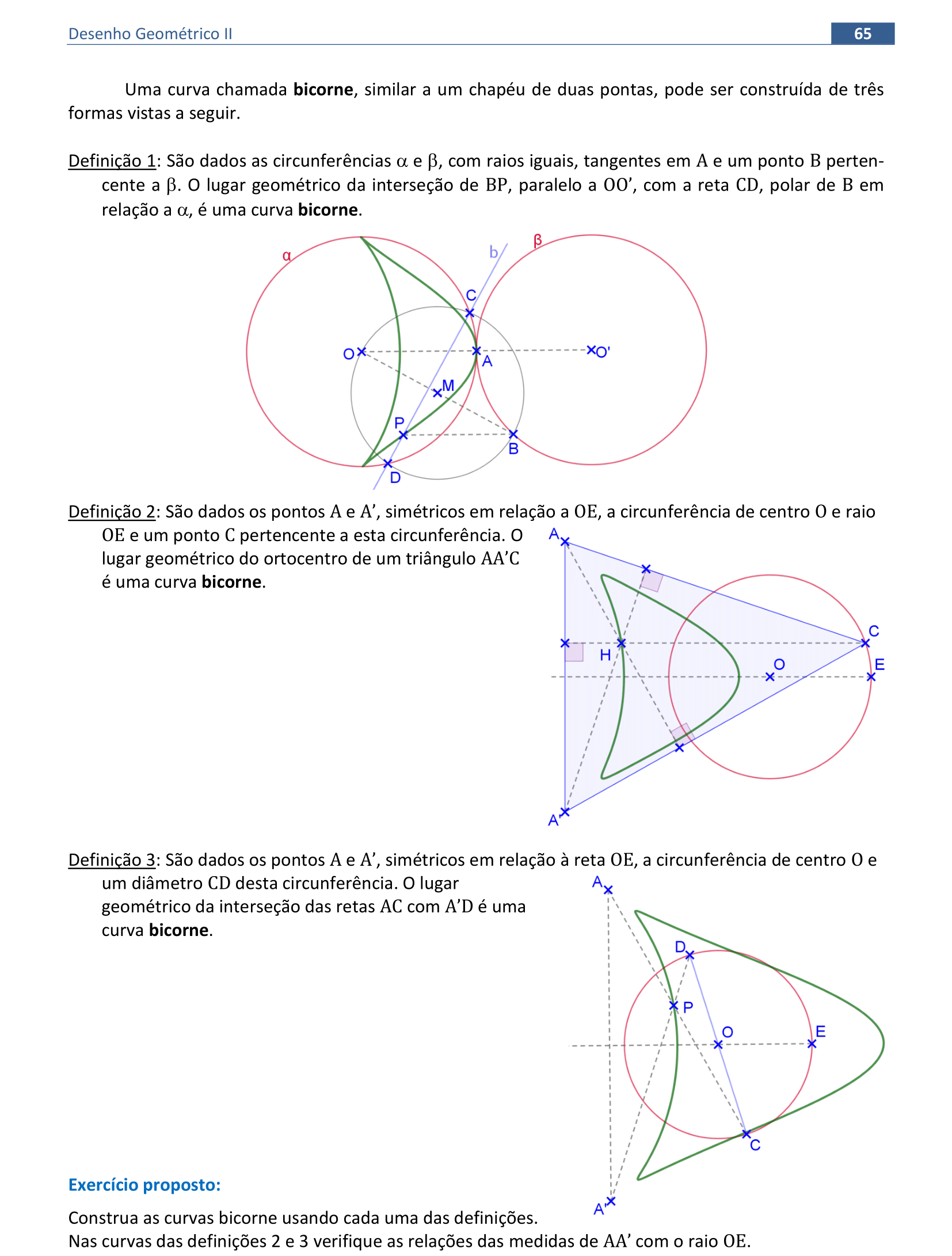
📏 📐 Resolução
Vamos construir a curva bicorne usando as três definições apresentadas nesta página.

📏 📐 Resolução
Vamos construir a curva lemniscata de Gerono usando as três definições apresentadas nesta página.

📏 📐 Resolução
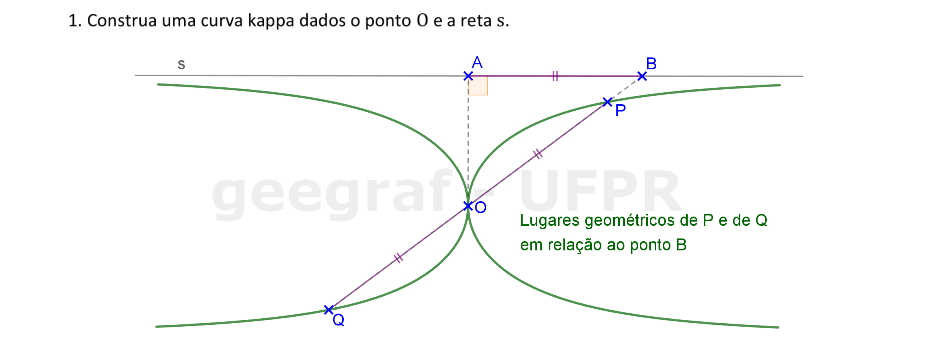
Vamos construir uma curva kappa, dados o ponto O e a reta s.


📏 📐 Resolução
Vamos construir a reta s da curva kappa, dados o ponto P da curva, a reta que contém o ponto A e o ponto O.


📏 📐 Resolução
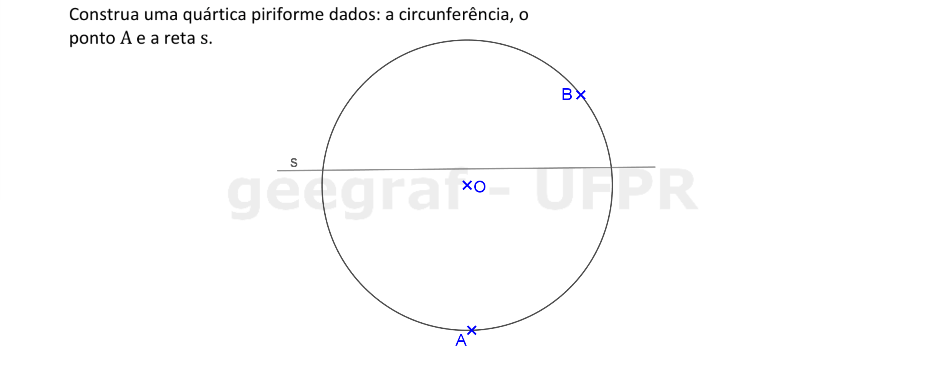
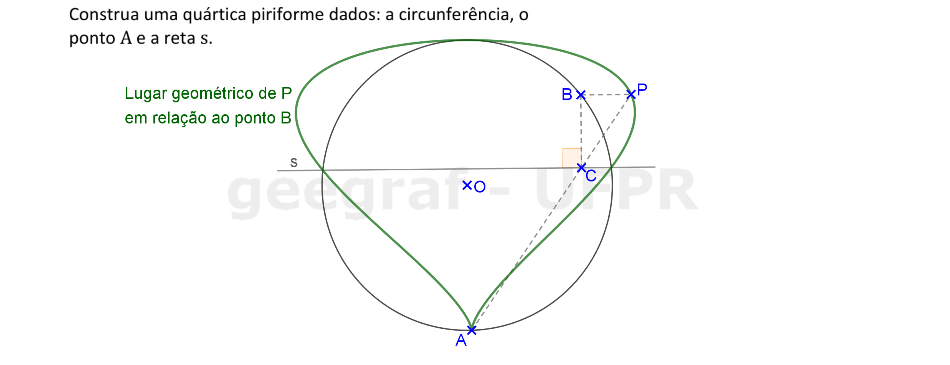
Vamos construir a curva quártica piriforme dados a circunferência, o ponto A e a reta s.

6. Curvas paramétricas
Material da página 68 até a página 79.

📏 📐 Resolução
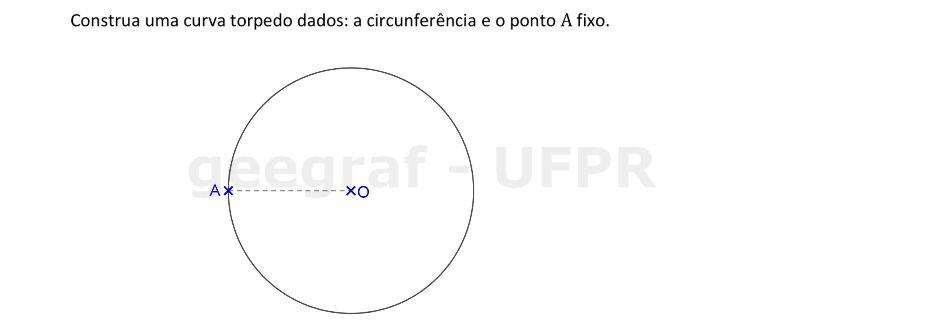
Vamos construir a curva torpedo dados a circunferência e o ponto fixo A.

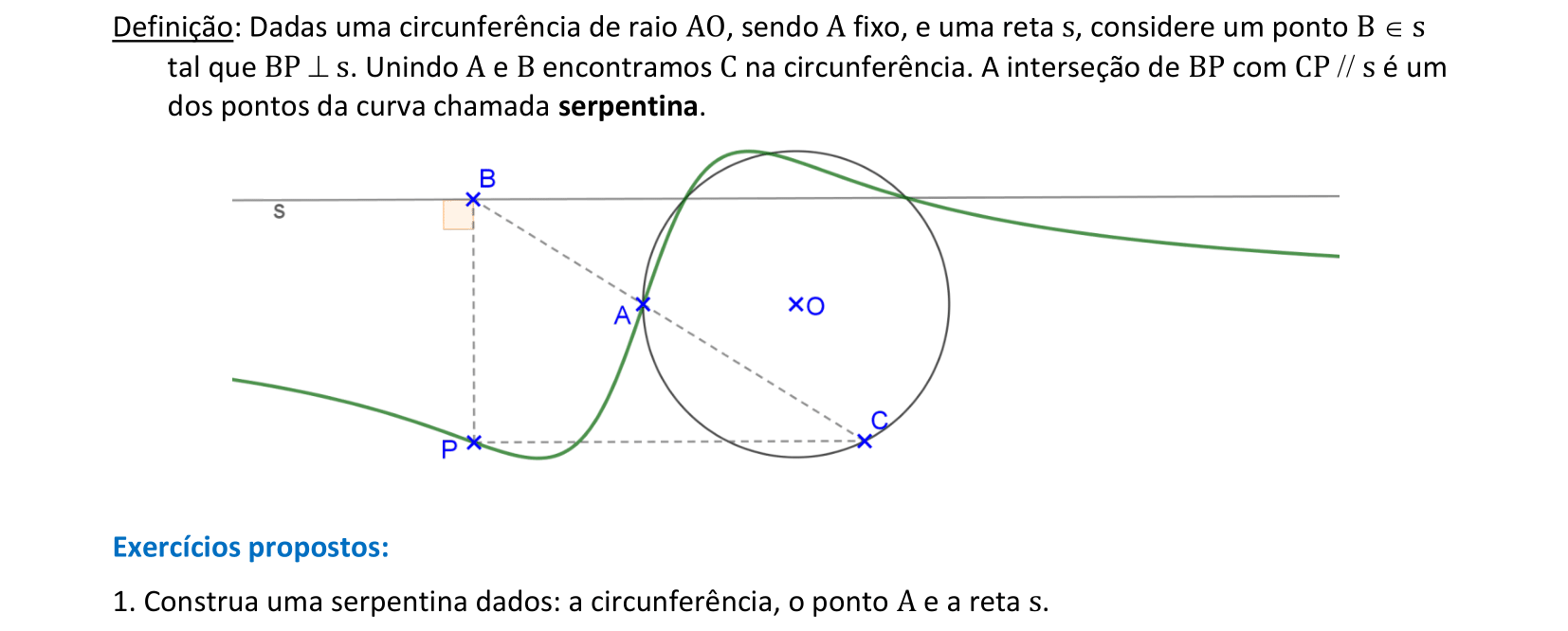
📏 📐 Resolução
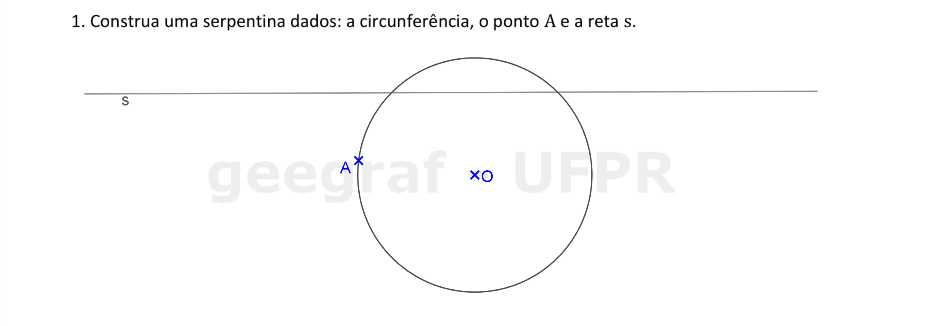
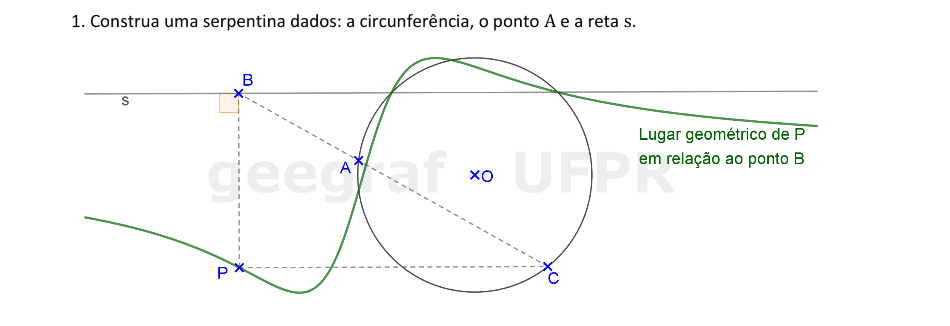
Vamos construir a curva serpentina dados a circunferência, o ponto A e a reta s.


📏 📐 Resolução
Vamos encontrar o ponto fixo que determine a curva serpentina, dados a circunferência, o ponto da curva P e a reta s.
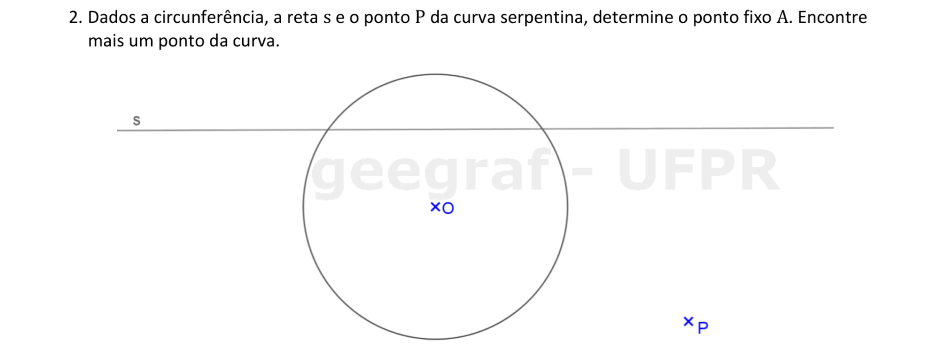

📏 📐 Resolução
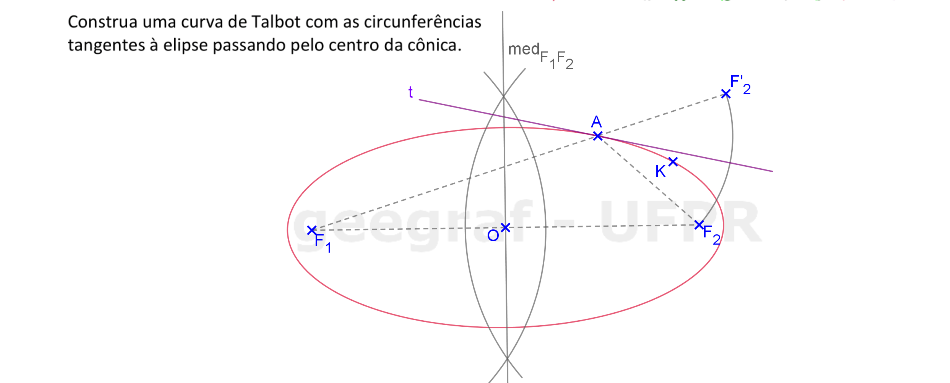
Vamos construir uma curva de Talbot com as circunferências tangentes à elipse passando pelo centro da elipse.

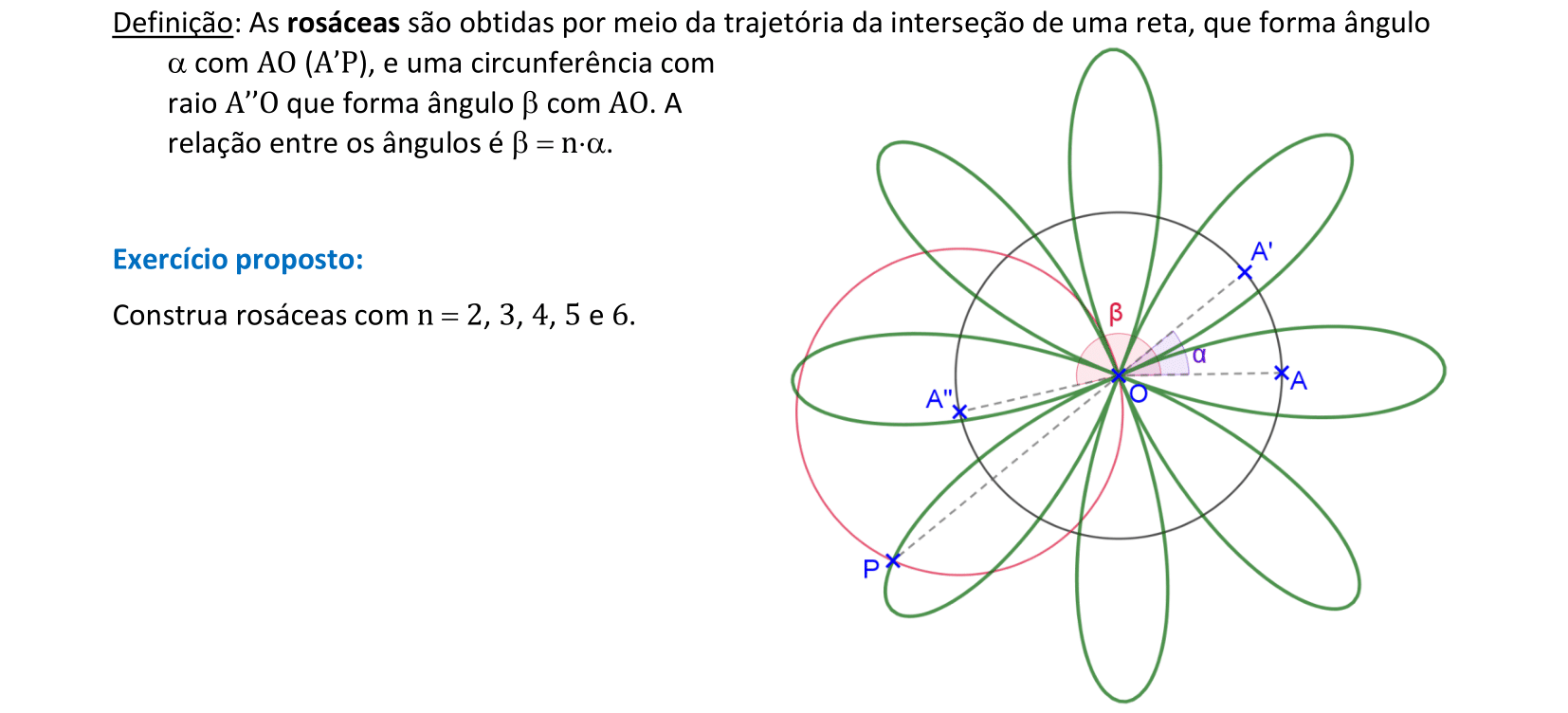
📏 📐 Resolução
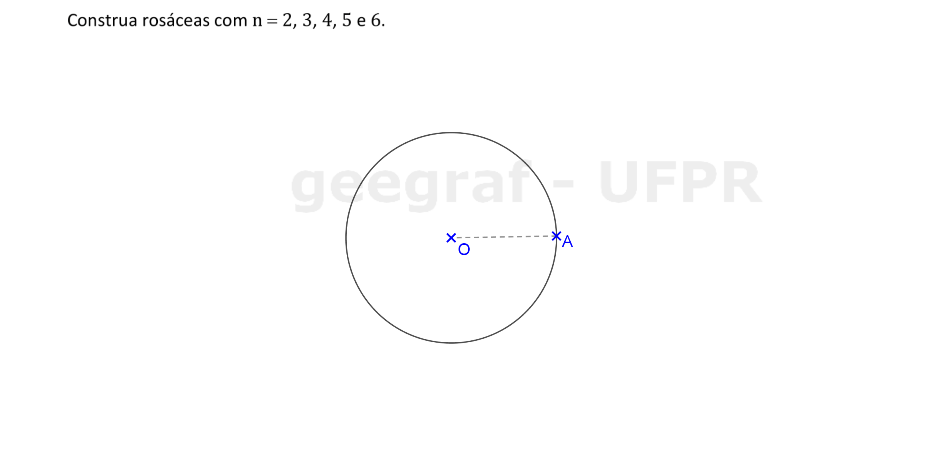
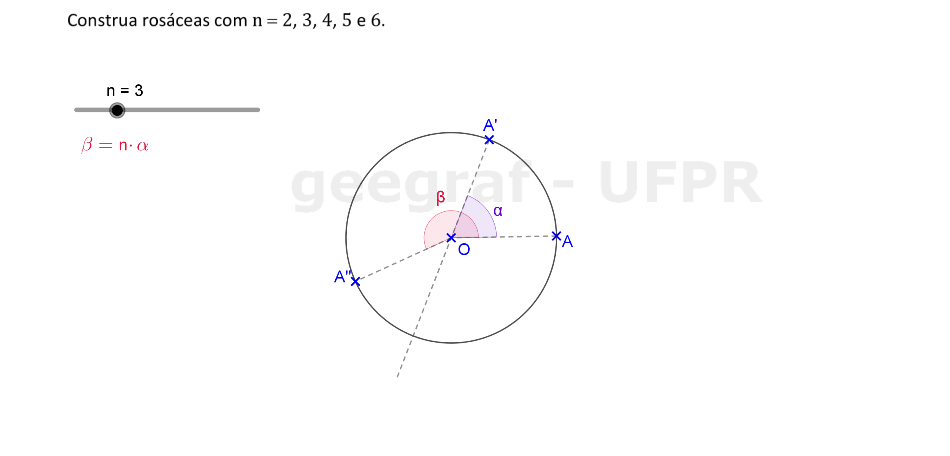
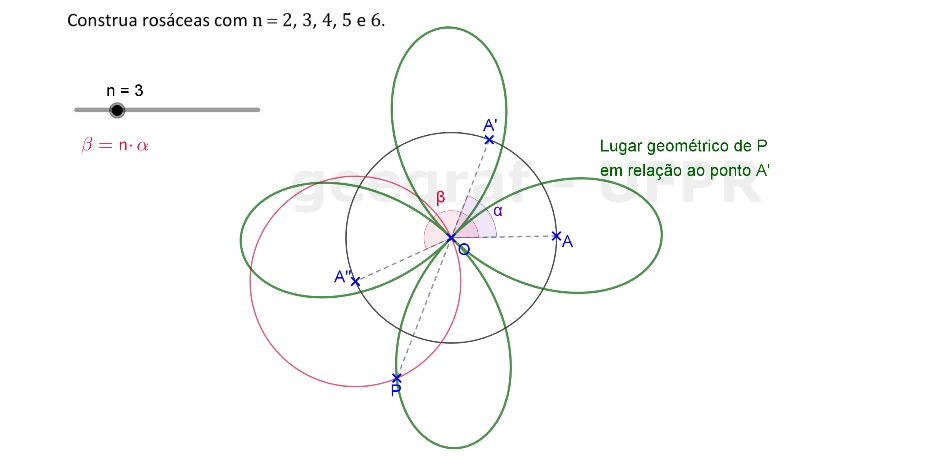
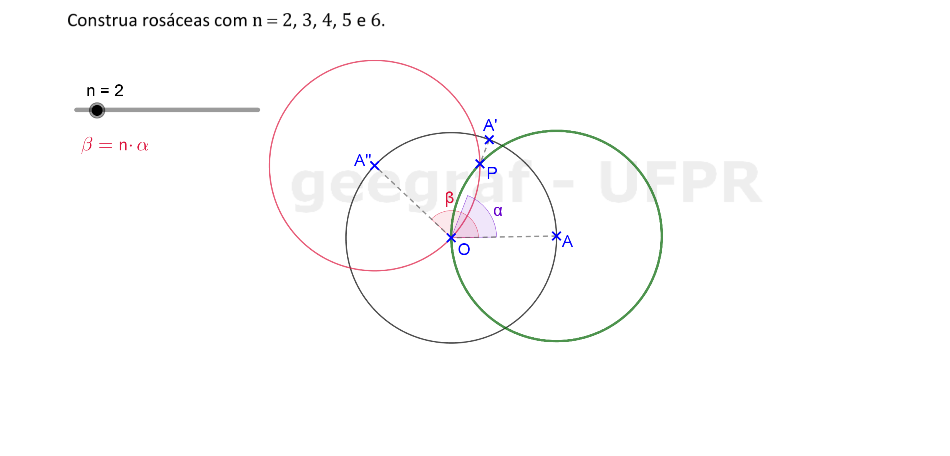
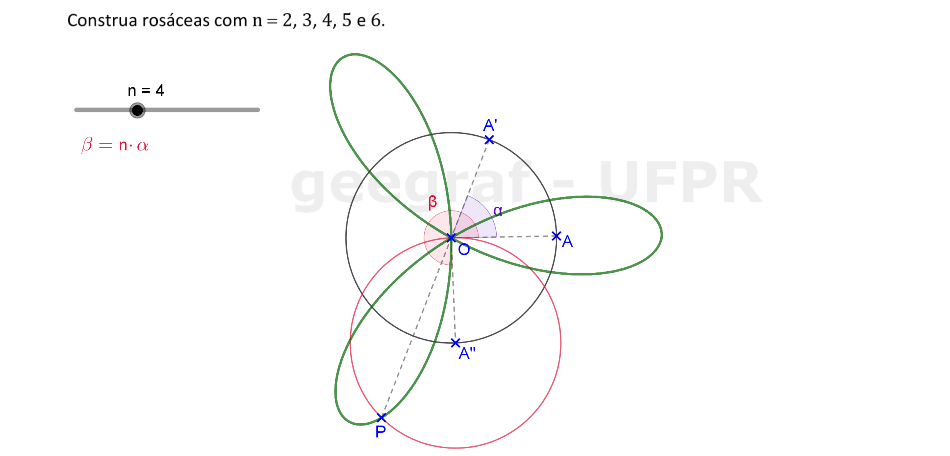
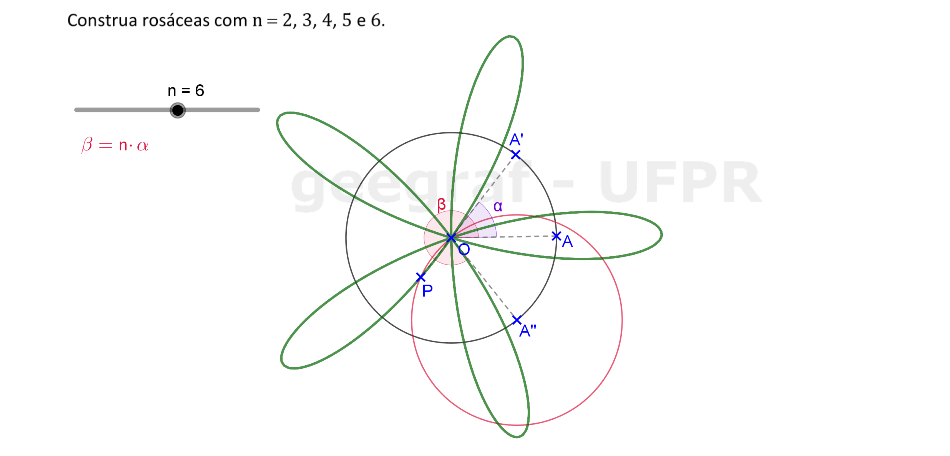
Vamos construir curvas rosáceas com n = 2, 3, 4, 5 e 6.

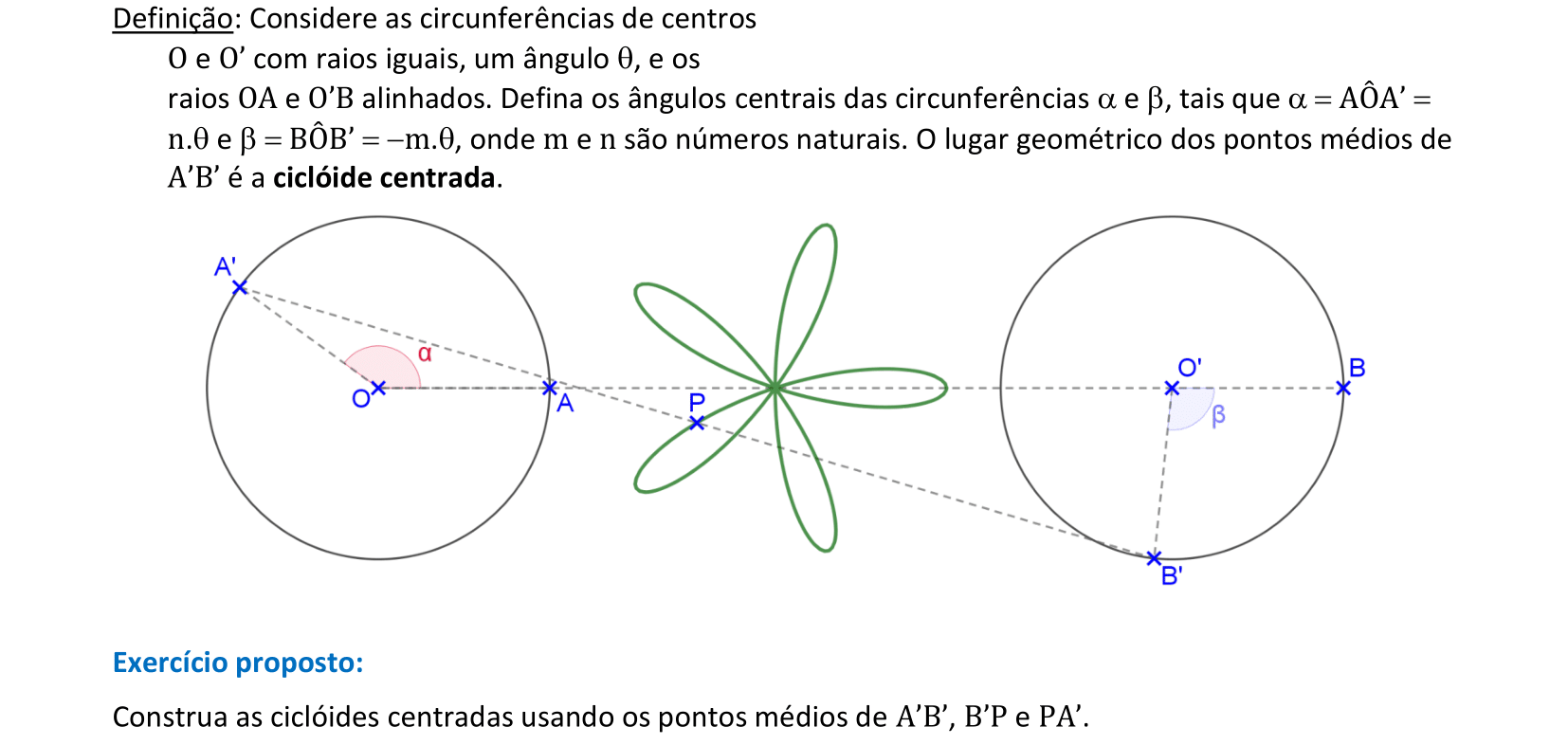
📏 📐 Resolução
Vamos construir as ciclóides centradas usando os pontos médios dos segmentos A'B', B'P e PA'.


📏 📐 Resolução
Vamos construir a curva bifolium usando as 3 definições mostradas nesta página.

📏 📐 Resolução
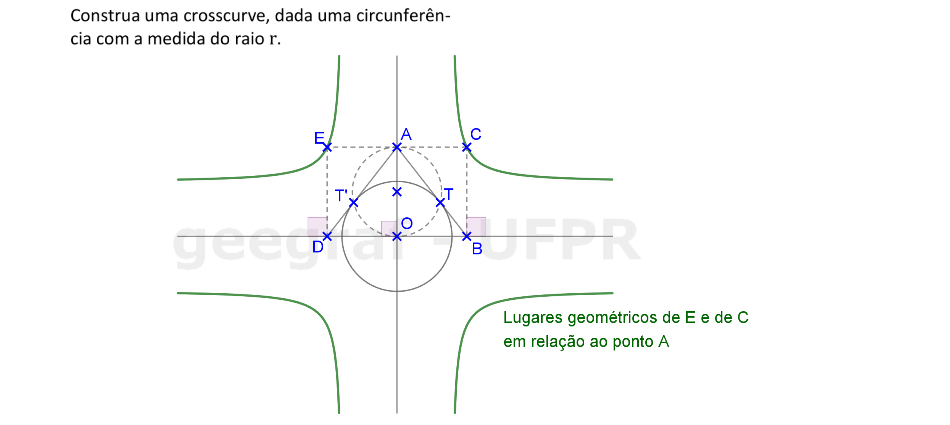
Vamos construir uma crosscurve a partir de uma circunferência.


📏 📐 Resolução
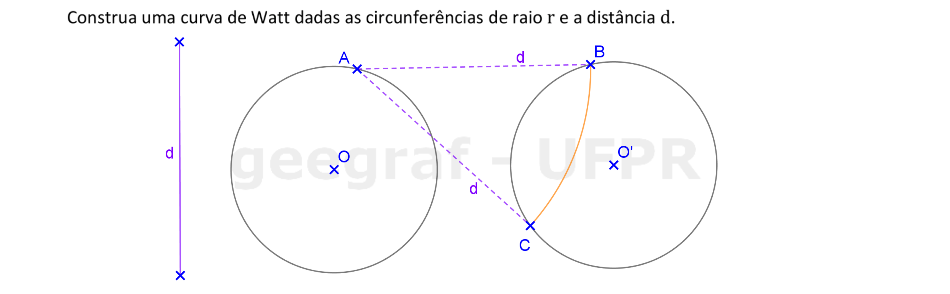
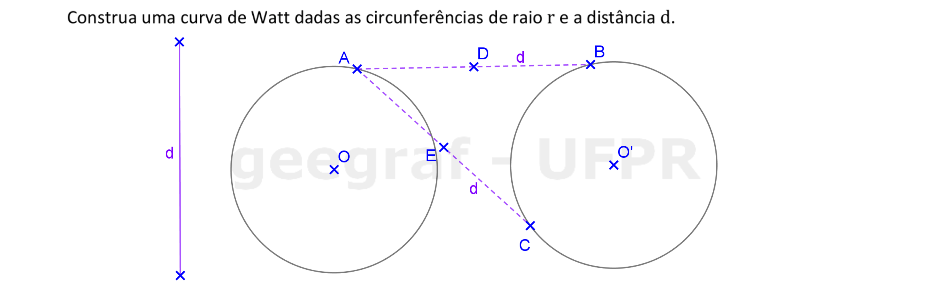
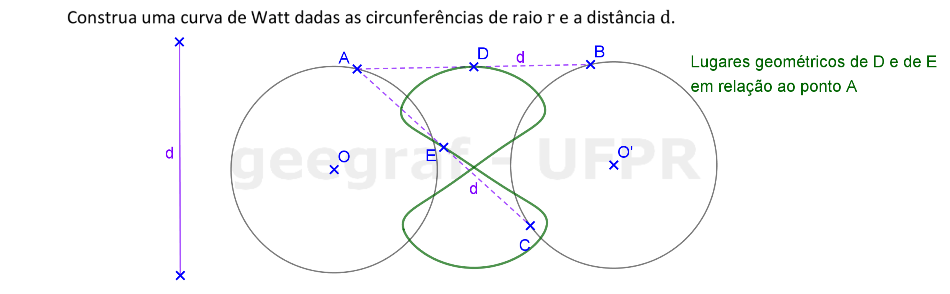
Vamos construir uma curva de Watt a partir das circunferências com raios de medida r e uma distância d.


📏 📐 Resolução
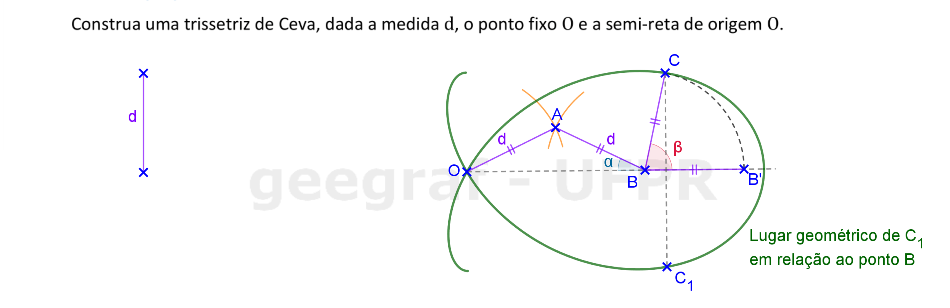
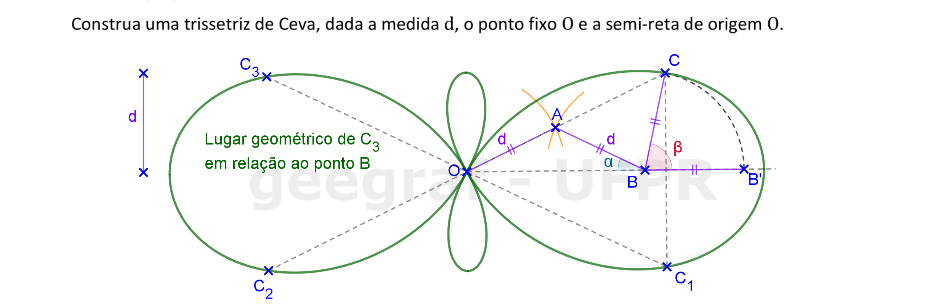
Vamos construir uma trissetriz de Ceva a partir de um ponto fixo O e uma distância d e a semi-reta de origem O.

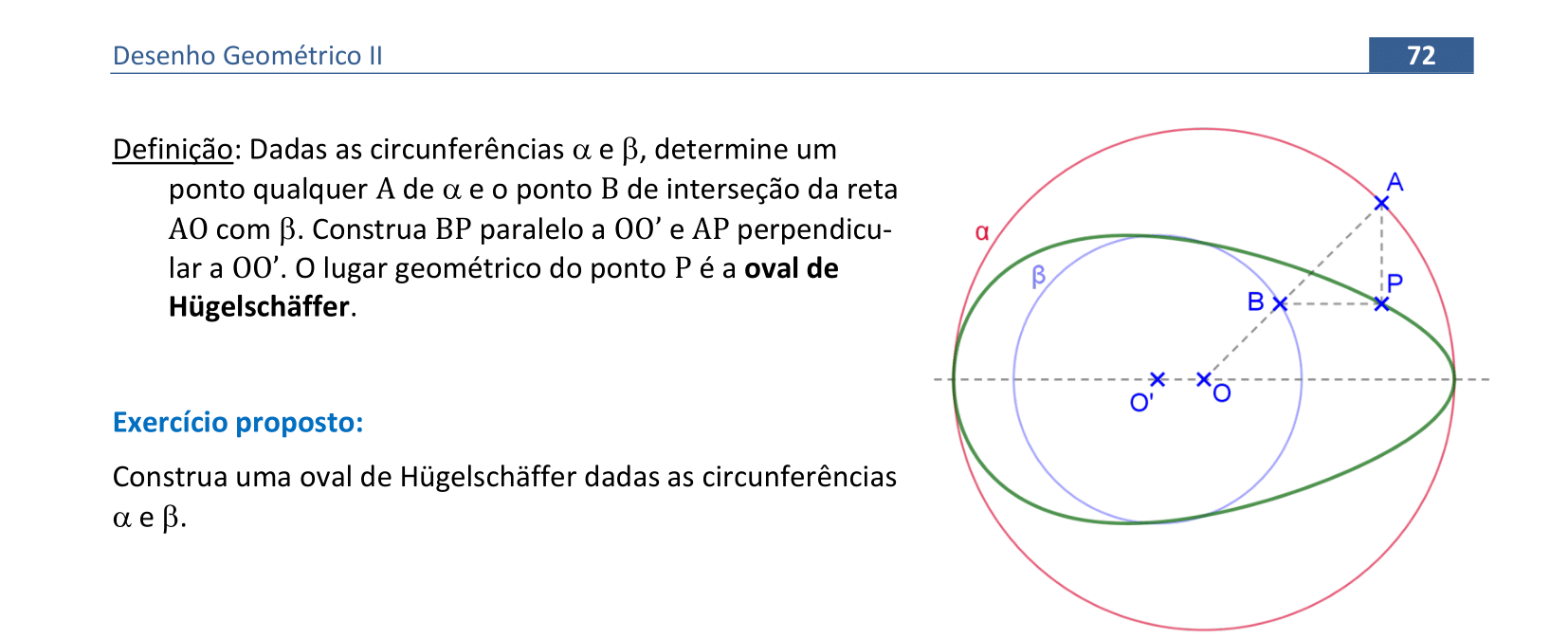
📏 📐 Resolução
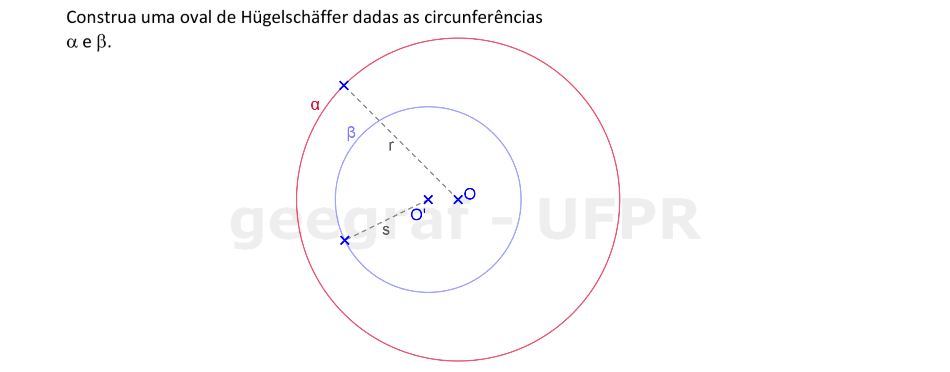
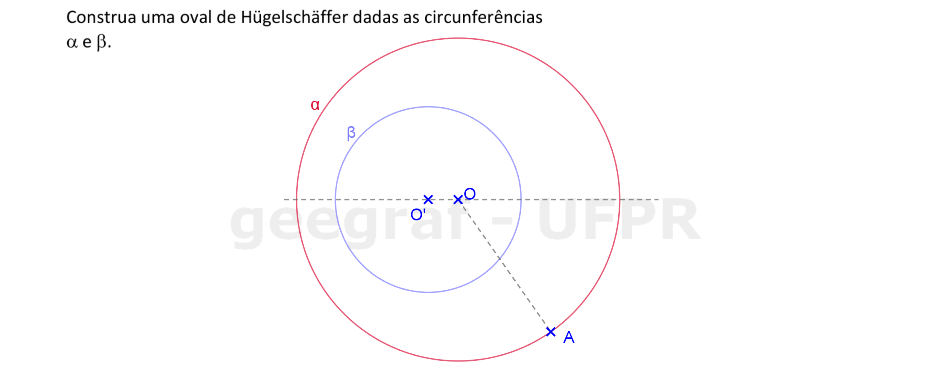
Vamos construir uma oval de Hügelschäffer a partir das circunferências α e β.


📏 📐 Resolução
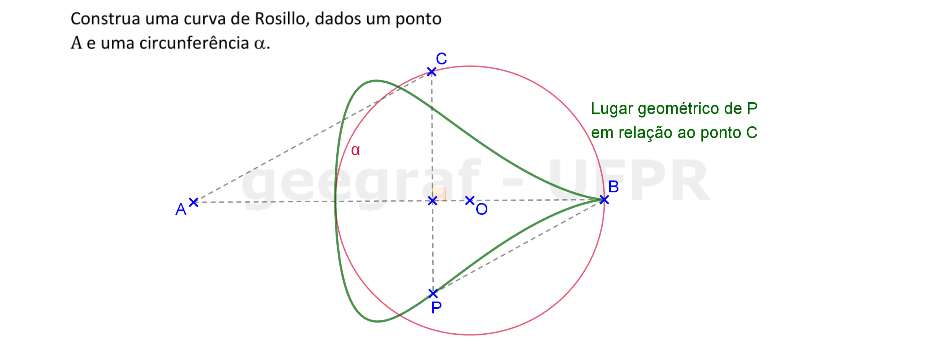
Vamos construir uma curva de Rosillo a partir da circunferência α e de um ponto A.

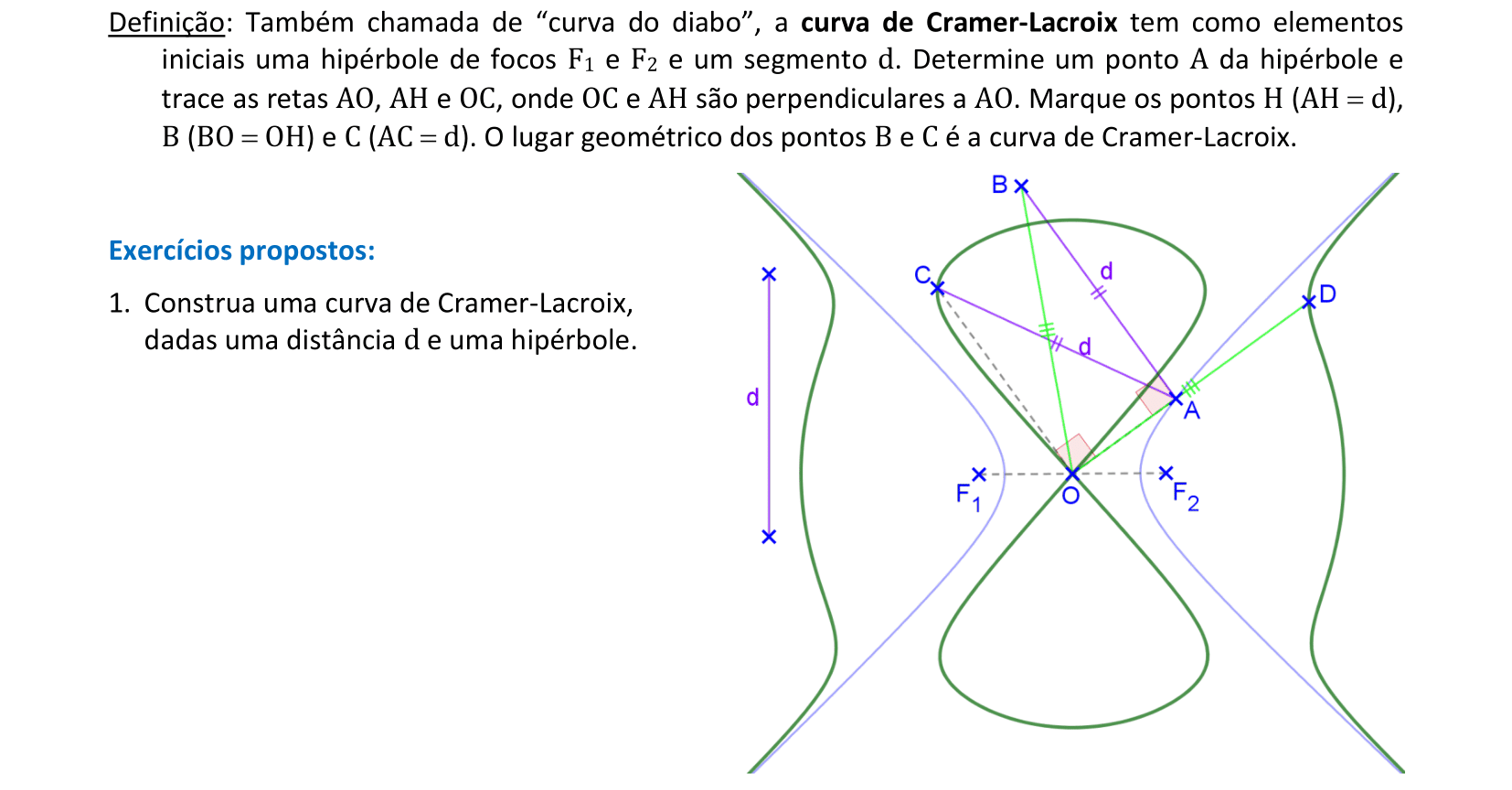
📏 📐 Resolução
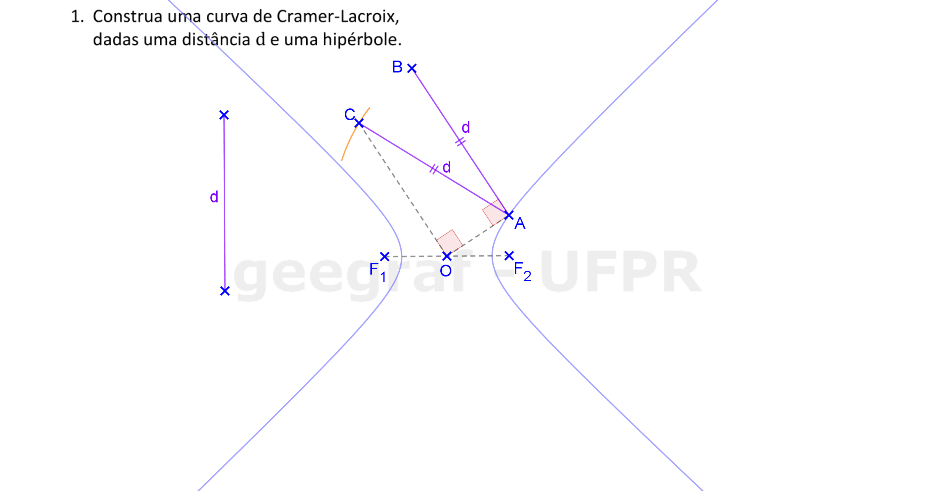
Vamos construir uma curva de Cramer-Lacroix a partir de uma hipérbole e de uma distância d.



📏 📐 Resolução
Vamos construir uma espiral de Euler a partir de um ponto A sobre o eixo x.


📏 📐 Resolução
Vamos construir uma espiral curva usando sua equação com coordenadas polares.

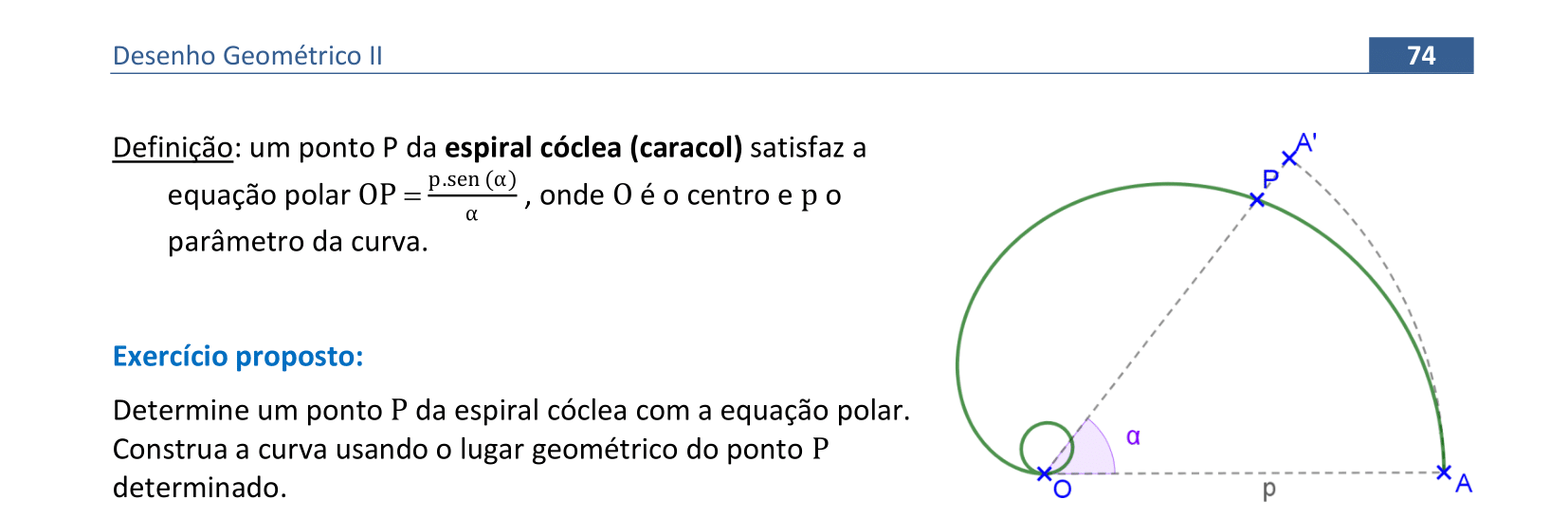
📏 📐 Resolução
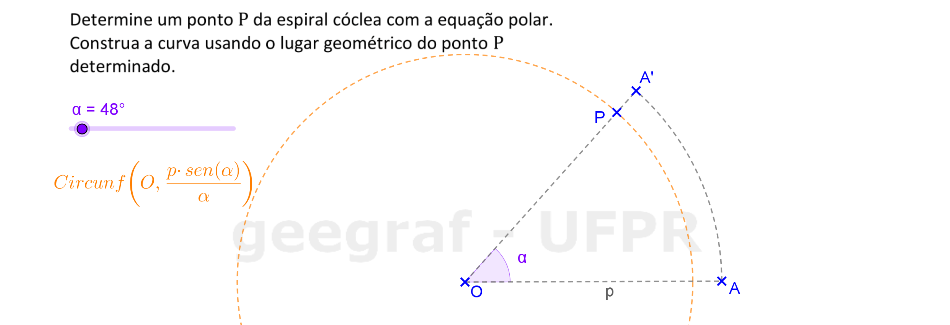
Vamos construir uma espiral cóclea usando sua equação com coordenadas polares.


📏 📐 Resolução
Vamos construir uma tratriz usando sua equação com coordenadas cartersianas.



📏 📐 Resolução
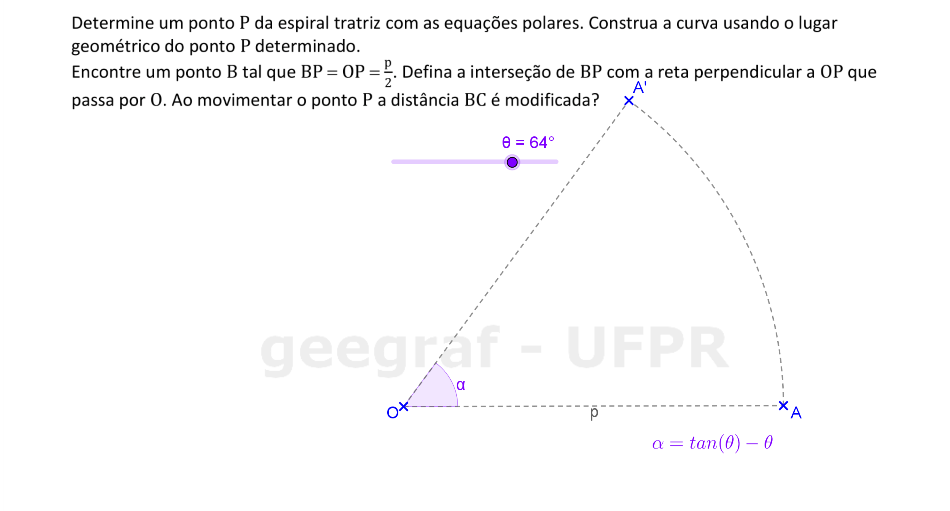
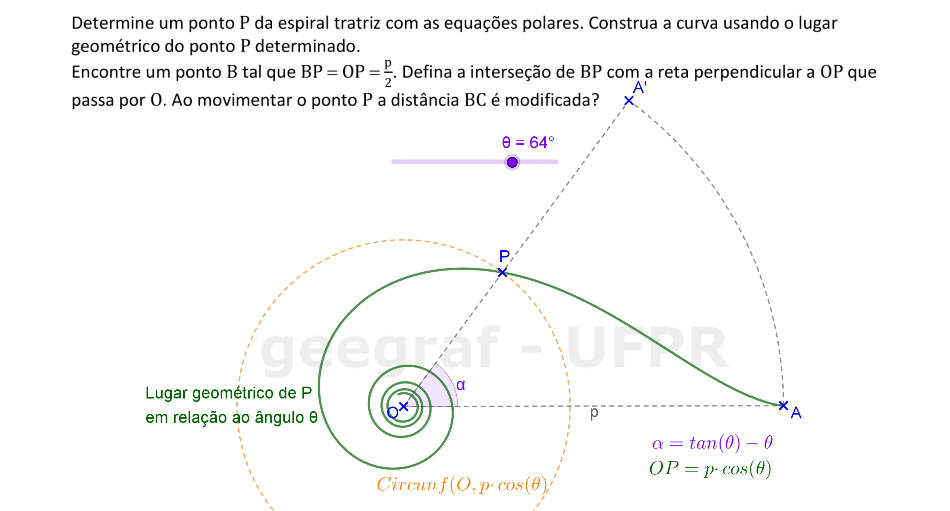
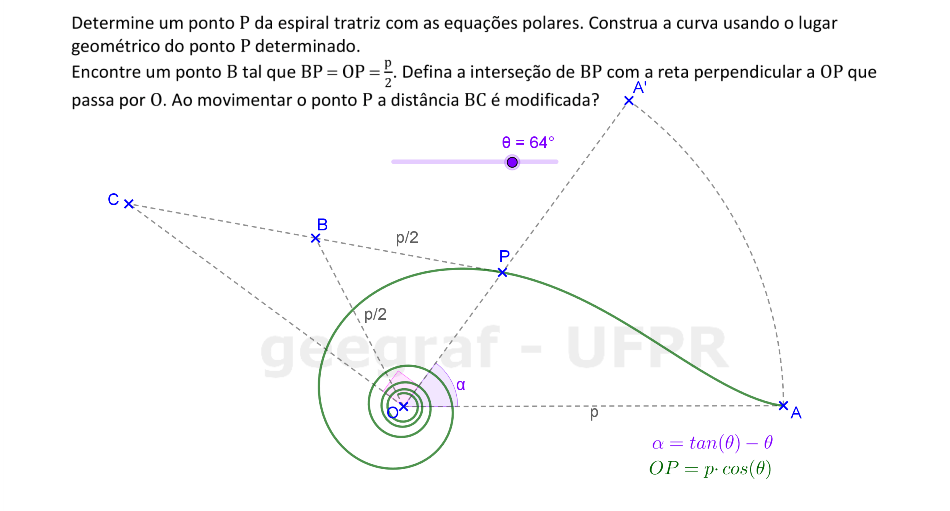
Vamos construir uma espiral tratriz usando suas equações com coordenadas polares.

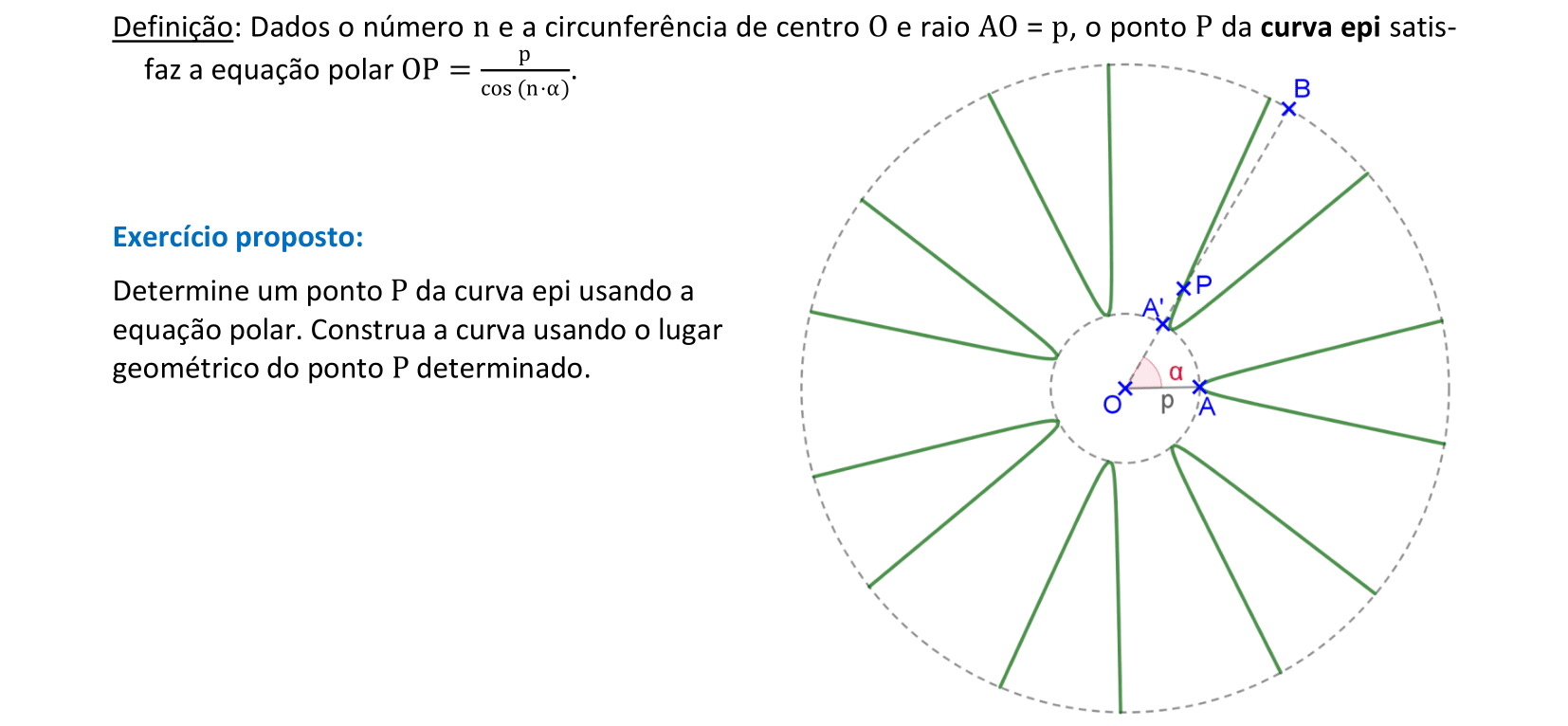
📏 📐 Resolução
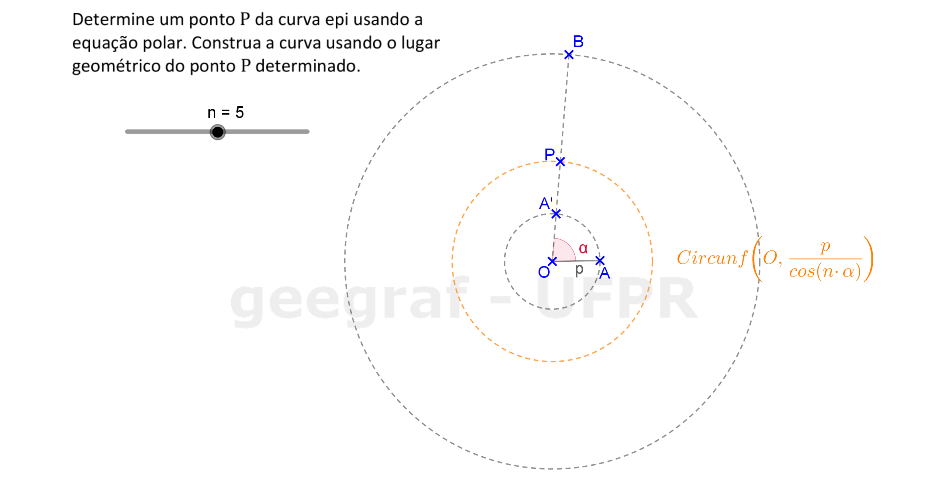
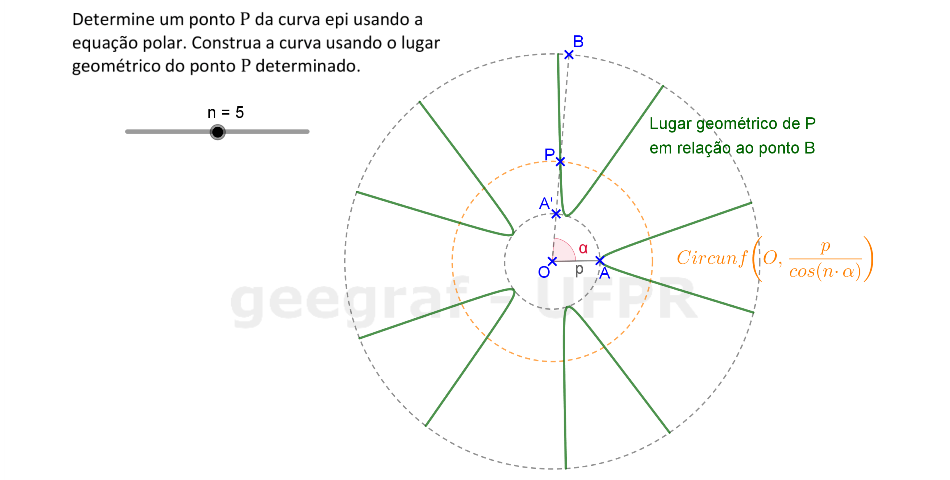
Vamos construir uma curva epi usando sua equação com coordenadas polares.

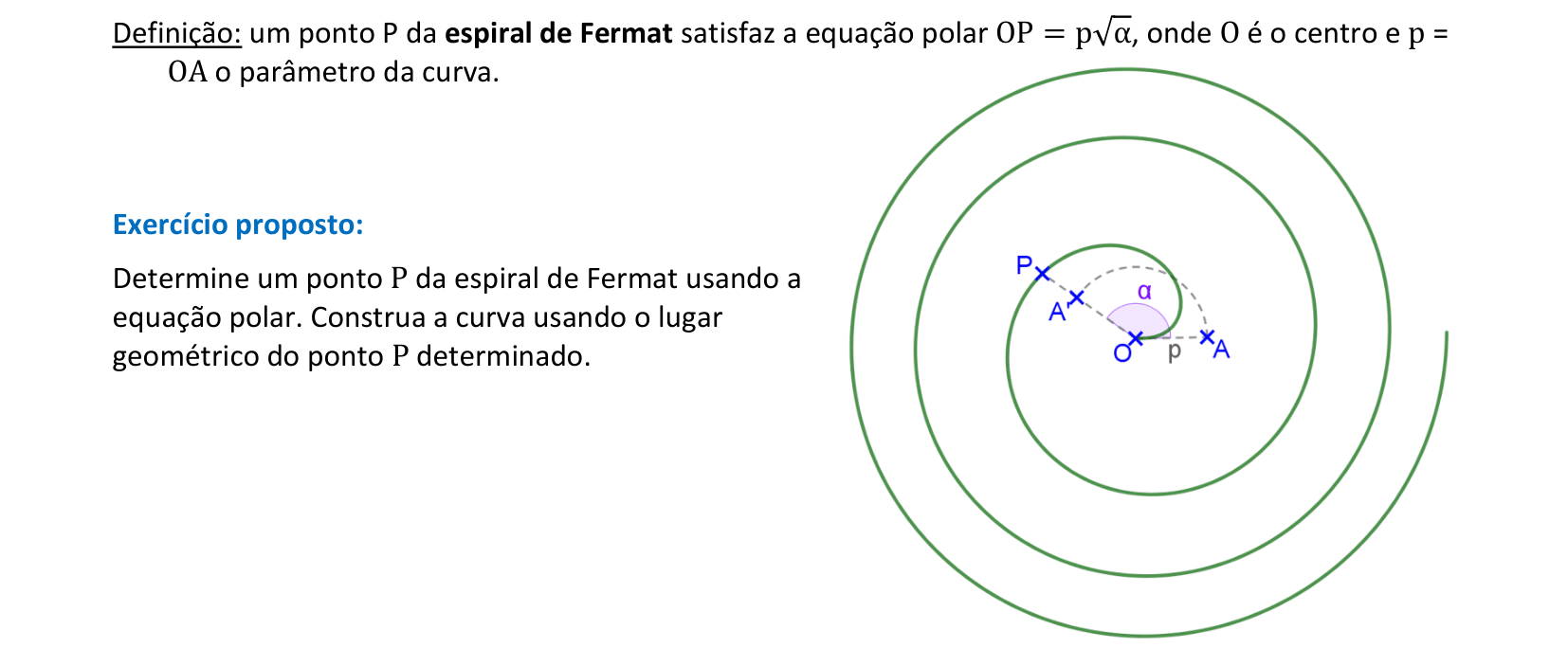
📏 📐 Resolução
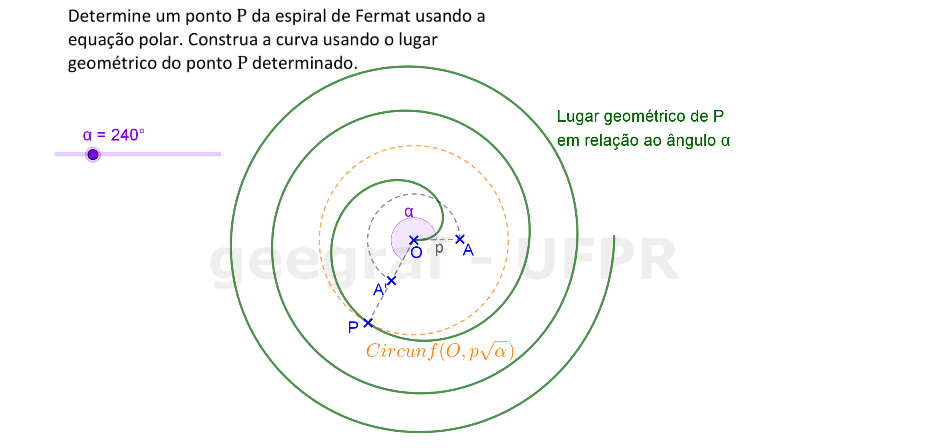
Vamos construir uma espiral de Fermat usando sua equação com coordenadas polares.

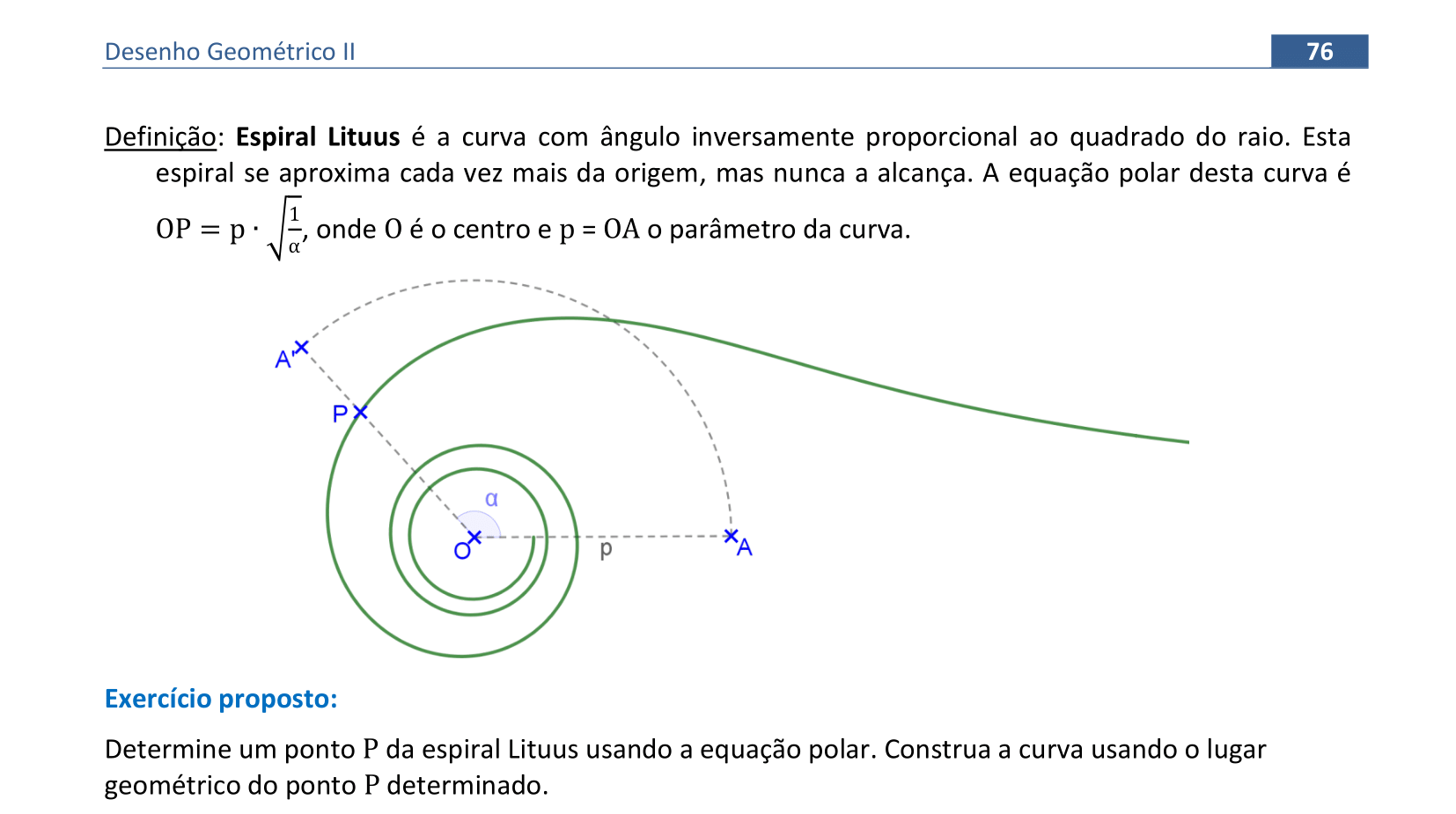
📏 📐 Resolução
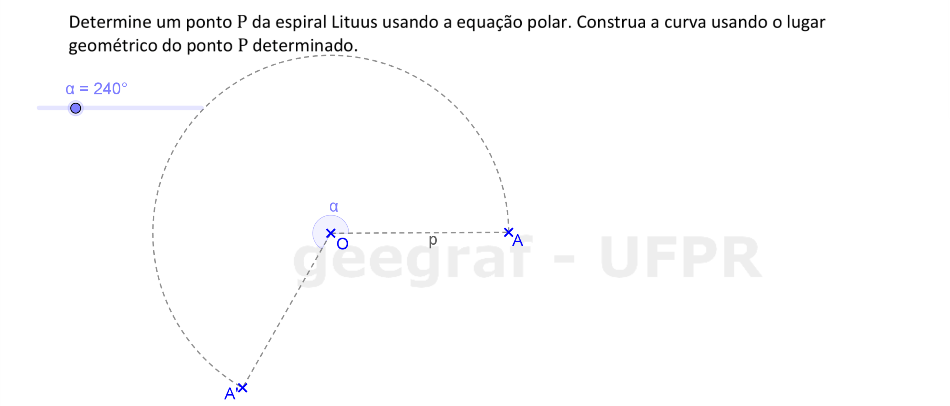
Vamos construir uma espiral Lituus usando sua equação com coordenadas polares.

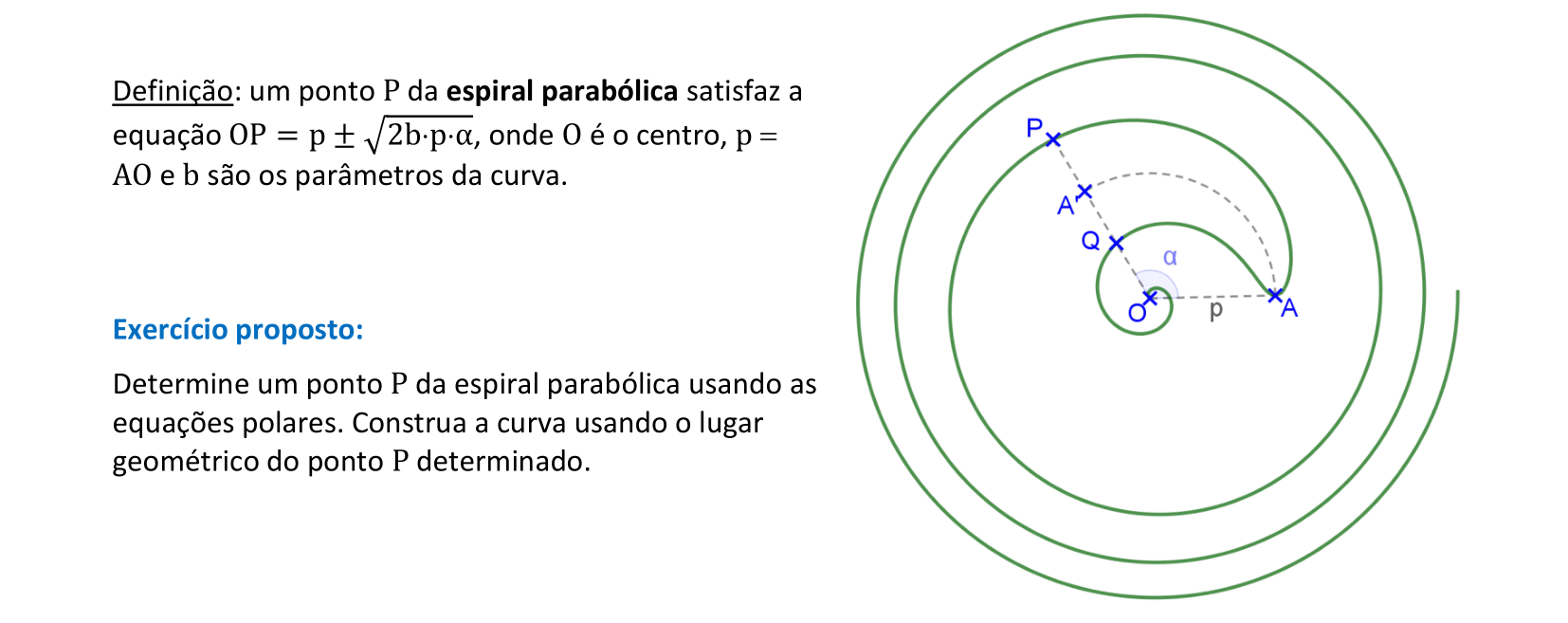
📏 📐 Resolução
Vamos construir uma espiral parabólica usando sua equação com coordenadas polares.

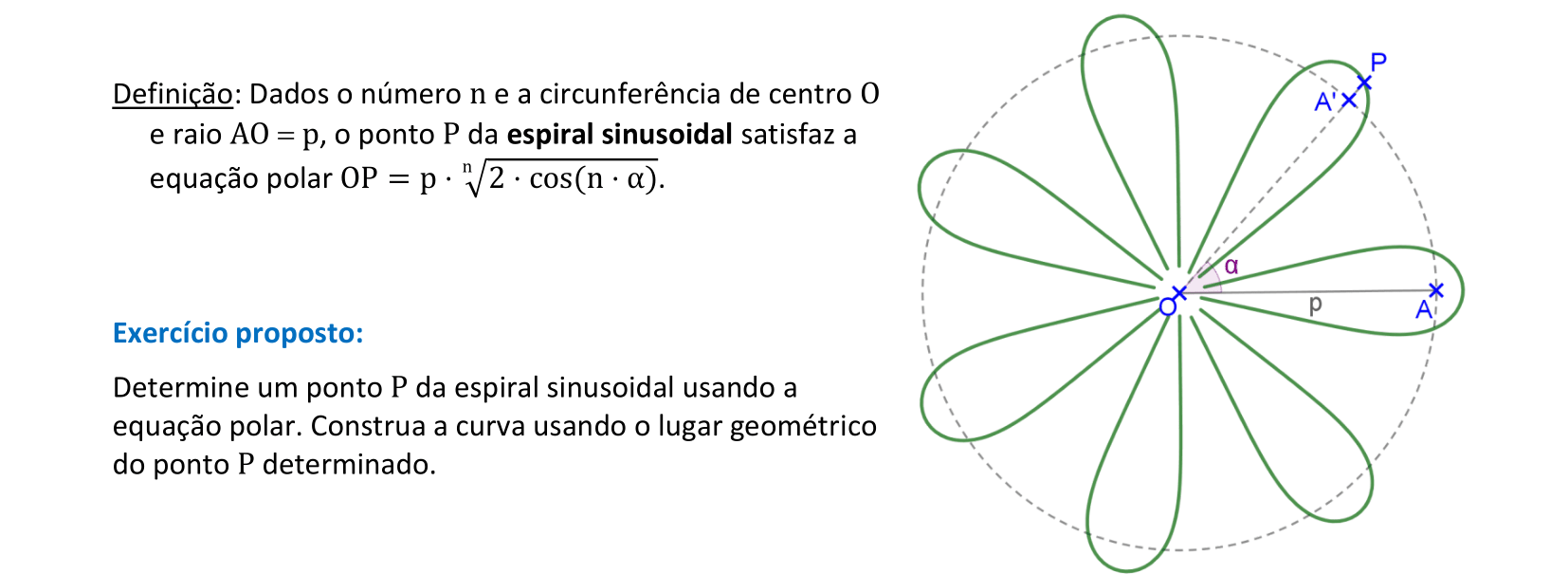
📏 📐 Resolução
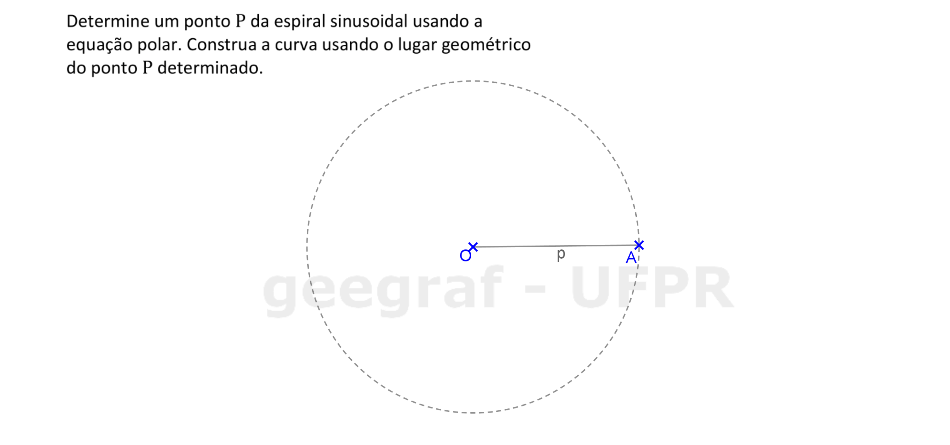
Vamos construir uma curva sinusoidal usando sua equação com coordenadas polares.


📏 📐 Resolução
Vamos construir uma curva folióide usando sua equação com coordenadas polares.

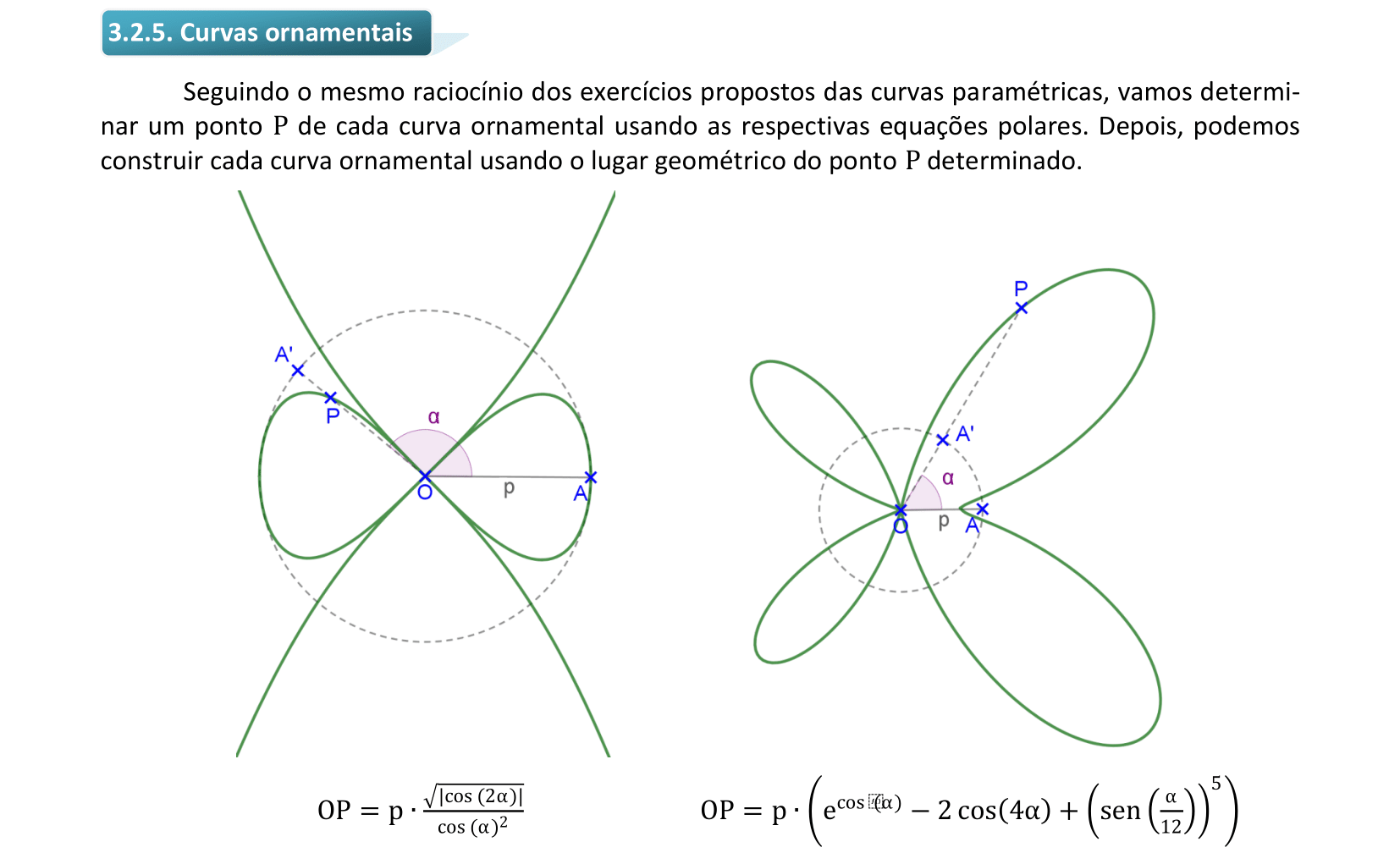
📏 📐 Resolução
Vamos construir curvas ornamentais usando suas equações com coordenadas polares.



📏 📐 Resolução
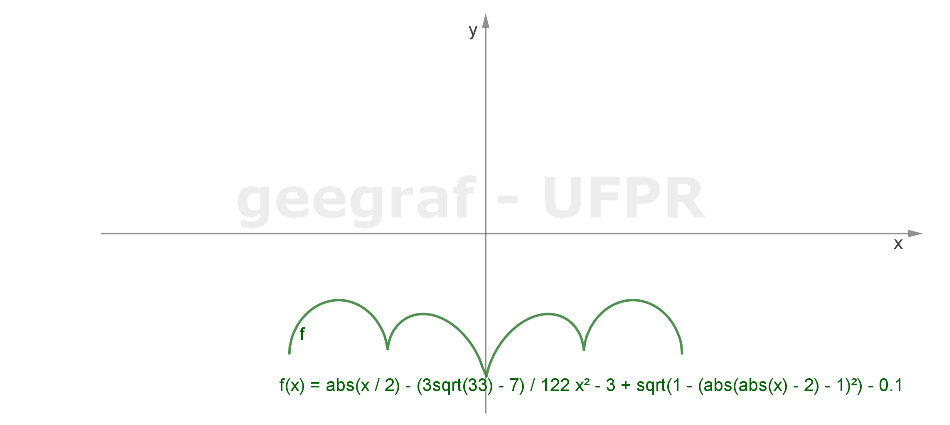
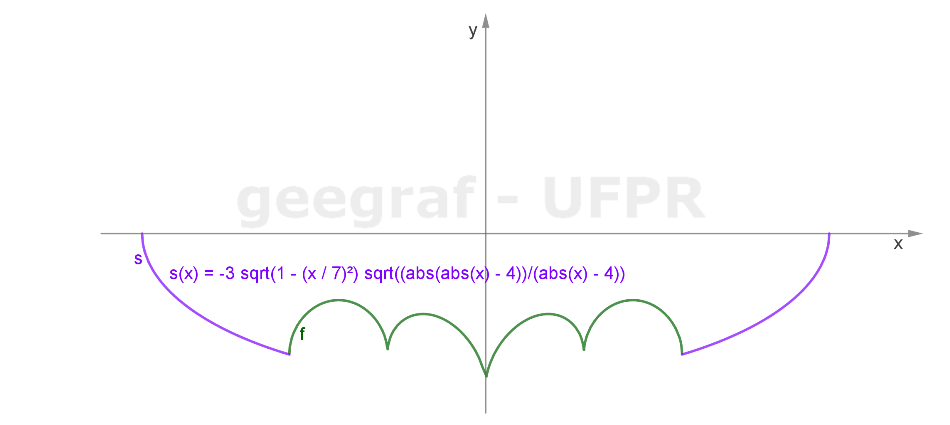
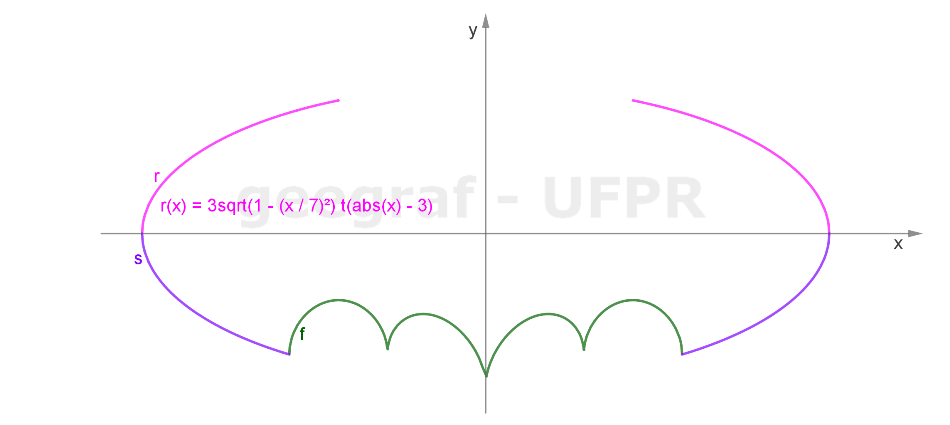
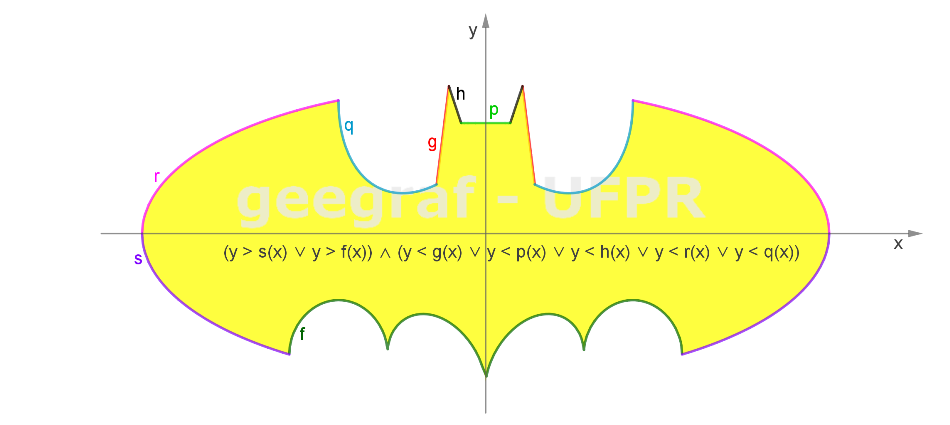
Vamos construir a curva do Batman usando funções com coordenadas cartesianas.


página desenvolvida por:
Paulo Henrique Siqueira
contato: paulohscwb@gmail.com
O desenvolvimento deste material de construções geométricas faz parte do Grupo de Estudos em Expressão Gráfica (GEEGRAF) da Universidade Federal do Paraná (UFPR)

Desenho Geométrico 2 de Paulo Henrique Siqueira está licenciado com uma Licença Creative Commons Atribuição-NãoComercial-SemDerivações 4.0 Internacional.
Como citar este trabalho:
Siqueira, P.H., "Desenho Geométrico 2". Disponível em: <https://paulohscwb.github.io/desenho-geometrico2/>, Dezembro de 2022.
Referências:
- Carvalho, B.A. Desenho Geométrico. Imperial Novo Milênio, 2008.
- Rezende, E.Q.F.; Queiroz, M.L.B. Geometria Euclidiana plana e construções geométricas. Editora da Unicamp, 2008.
- Marmo, C.M.B. Curso de Desenho, vol. 1 a 4. Editora Moderna, 1967.
- Braga, T.B. Desenho Linear Geométrico. Editora Cone, 1997.
- Braga, T.B. Problemas de Desenho Linear Geométrico. Cultura Brasileira, 1962.
- Candido Gomes, M.E. Desenho Geométrico. Editora I.T.E.C., 1950.
- Giovanny, J.R. Desenho Geométrico, vol.4. Editora FTD, 1996.
- Putnoki, J.C. Elementos de Geometria e Desenho Geométrico. v. 1-3. Scipione, 1993.
- Siqueira, P.H.; Costa, D.M.B. Apostila de Desenho Geométrico 2. UFPR, 2022.